堆排序可以看作顺序存储的完全二叉树。
堆排序属于选择排序的一种,
选择排序:每一趟在待排序元素中选取关键字最小(或最大)的元素加入有序子序列。
1.堆的定义
若n个关键字序列 L [ 1... n ] L[ 1...n] L[1...n]满足下面某一条性质,则称为堆(Heap) :
- 若满足∶ L ( i ) ≥ L ( 2 i ) 且 L ( i ) ≥ L ( 2 i + 1 ) ( 1 ≤ i ≤ n / 2 ) L(i)≥L(2i)且L(i)≥L(2i+1) (1 ≤i ≤n/2 ) L(i)≥L(2i)且L(i)≥L(2i+1)(1≤i≤n/2) :大根堆(大顶堆)
- 若满足: L ( i ) ≤ L ( 2 i ) 且 L ( i ) ≤ L ( 2 i + 1 ) ( 1 ≤ i ≤ n / 2 ) L(i)≤L(2i)且L(i)≤L(2i+1) (1 ≤i ≤n/2 ) L(i)≤L(2i)且L(i)≤L(2i+1)(1≤i≤n/2) :小根堆(小顶堆)
堆可以看作是一个完全二叉树的排列:
- 大根堆:完全二叉树中,根≥左、右。‘
- 小根堆︰完全二叉树中,根≤左、右。
1.与二叉树的顺序存储的联系
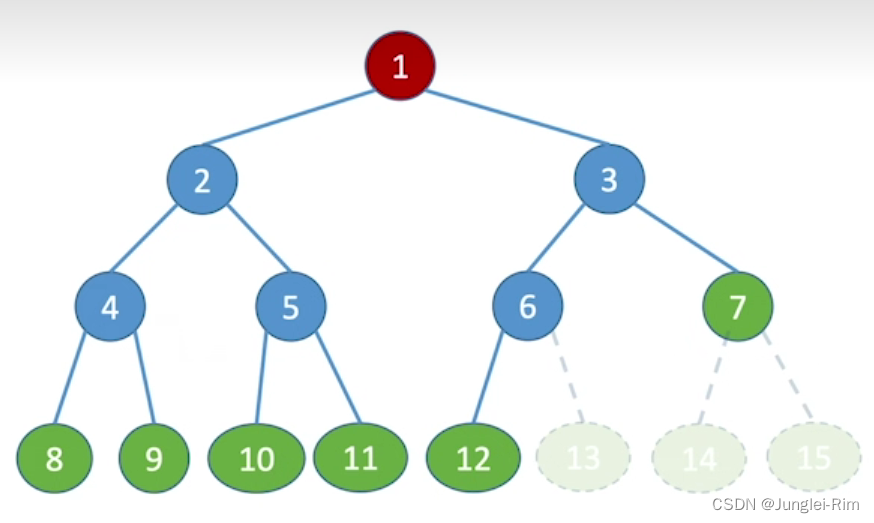
层序遍历以下二叉树:
1.常考的基本操作:
- i的左孩子: 2 i 2i 2i
- i的右孩子: 2 i + 1 2i+1 2i+1
- i的父节点: [ i 2 ] [\frac{i}{2}] [2i](向下取整)
- i所在的层次: l o g 2 ( n + 1 ) 或 [ l o g 2 n ] ( 向下取整 ) + 1 log_2(n + 1)或[log_2n](向下取整)+ 1 log2(n+1)或[log2n](向下取整)+1
2.若完全二叉树中共有n个结点,则
- 判断i是否有左孩子: 2 i < = n 2i<=n 2i<=n
- 判断i是否有右孩子: 2 i + 1 < = n 2i+1<=n 2i+1<=n
- 判断i是否是叶子/分支结点?: i > [ n / 2 ] ( 向下取整 ) i > [n/2](向下取整) i>[n/2](向下取整)
2.建立大根堆
根据大根堆的特性︰ 根 ≥ 左、右 根≥左、右 根≥左、右
1.思路
- 把所有非终端结点都检查一遍,是否满足大根堆的要求,如果不满足,则进行调整
- 检查当前结点是否满足根≥左、右,
- 若不满足,将当前结点与更大的一个孩子互换.
- 若元素互换破坏了下一级的堆,则采用相同的方法继续往下调整(小元素不断“下坠”)
2.代码实现
//将以k 为根的子树调整为大根堆
void HeadAdjust(int A[], int k, int len) {
A[0] = A[k];//A[0]暂存子树的根结点
for (int i = 2 * k; i <= len; i *= 2) {
//汇key较大的子结点向下筛选
if (i < len && A[i] < A[i + 1])
i++;//取key较大的子结点的下标
if (A[0] >= A[i])break;//筛选结束
else {
A[k] = A[i];//将A[i]调整到双亲结点上
k = i;//修改k值,以便继续向下筛选
}
}
A[k] = A[0];//被筛选结点的值放入最终位置
}
//建立大根堆
void BuildMaxHeap(int A[], int len) {
for (int i = len / 2; i > 0; i--)//从后往前调整所有非终端结点
HeadAdjust(A, i, len);
}
3.基于大根堆进行排序
1.原理
- 堆排序:每一趟将堆顶元素加入有序子序列(与待排序序列中的最后一个元素交换)
- 并将待排序元素序列再次调整为大根堆(小元素不断“下坠”)
- 注意:基于大根堆的堆排序得到“递增序列”,基于小根堆的堆排序得到“递减序列”。
2.代码实现
//堆排序的完整逻辑
void HeapSort(int A[], int len) {
BuildMaxHeap(A, len);//初始建堆
for (int i = len; i > 1; i--) {// n-1趟的交换和建堆过程
swap(A[i], A[1]);//堆顶元素和堆底元素交换
HeadAdjust(A, 1, i - 1);//把剩余的待排序元素整理成堆
}
}
4.算法效率分析
1.建堆过程的分析
- 若当前结点下方有两个孩子,则“下坠”一层,需对比关键字2次。
- 若下方只有一个孩子,则“下坠”一层,只需对比关键字1次。
- 结论:一个结点,每“下坠”一层,最多只需对比关键字2次
- 若树高为h,某结点在第i层,则将这个结点向下调整最多只需要“下坠” h-i层,
- 关键字对比次数不超过2(h-i)
- n个结点的完全二叉树树高h= [ l o g 2 n ] ( 向下取整 ) + 1 [log_2n](向下取整) +1 [log2n](向下取整)+1
- 第i层最多有2-1个结点,而只有第1~(h-1)层的结点才有可能需要“下坠”调整
结论:
- 将整棵树调整为大根堆,关键字对比次数不超过4n.
- 建堆过程,关键字对比次数不超过4n,建堆时间复杂度=O(n)
2.堆排序的过程分析
- 根节点最多下坠h-1层,每下坠一层,
- 而每“下坠”一层,最多只需对比关键字2次,
- 因此每一趟排序复杂度不超过 O ( h ) = O ( l o g 2 n ) O(h)= O(log_2n) O(h)=O(log2n)
- 共n-1趟,总的时间复杂度= O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)
因此堆排序的时间为建堆的时间加上排序的时间:
- 堆排序的时间复杂度= O ( n ) + O ( n l o g 2 n ) = O ( n l o g 2 n ) O(n)+O(nlog_2n)= O(nlog_2n) O(n)+O(nlog2n)=O(nlog2n),
- 堆排序的空间复杂度= O ( 1 ) O(1) O(1).
5.稳定性
根据代码:若左右孩子一样大,则优先和左孩子交换。
结论:不稳定。
6.在堆中插入新元素
寻找完全二叉树中相关结点的方法:
- i的左孩子:2i
- i的右孩子:2i+1
- i的父节点:[i/2](向下取整)
1.对小根堆进行插入
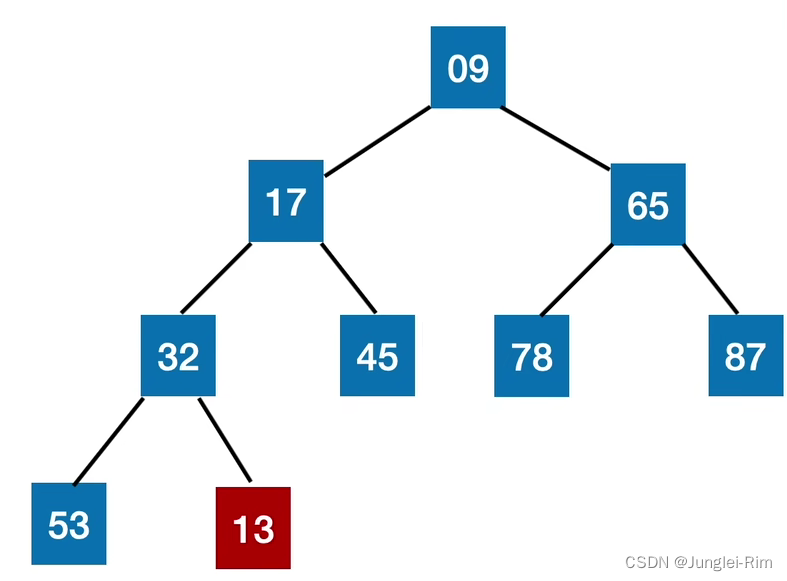
- 对于小根堆,新元素放到表尾,与父节点对比,
- 若新元素比父节点更小,则将二者互换。
- 新元素就这样一路“上升”,直到无法继续上升为止
7.在堆中删除元素
1.对小根堆进行删除
被删除的元素用堆底元素替代,然后让该元素不断“下坠”,直到无法下坠为止。
2.关键字对比次数分析
- 每次“上升”调整只需对比关键字1次
- 每次“下坠”调整可能需要对比关键字2次,也可能只需对比1次

![心法利器[102] | 大模型落地应用架构的一种模式](https://img-blog.csdnimg.cn/img_convert/d68608422e0b7ee9f14842601f5c705d.png)