第一章 神经网络是如何实现的

神经网络只是提供了一个一般性方法，具体用它求解什么问题，根据问题的特点，定义好输入输出以及损失函数就可以了。

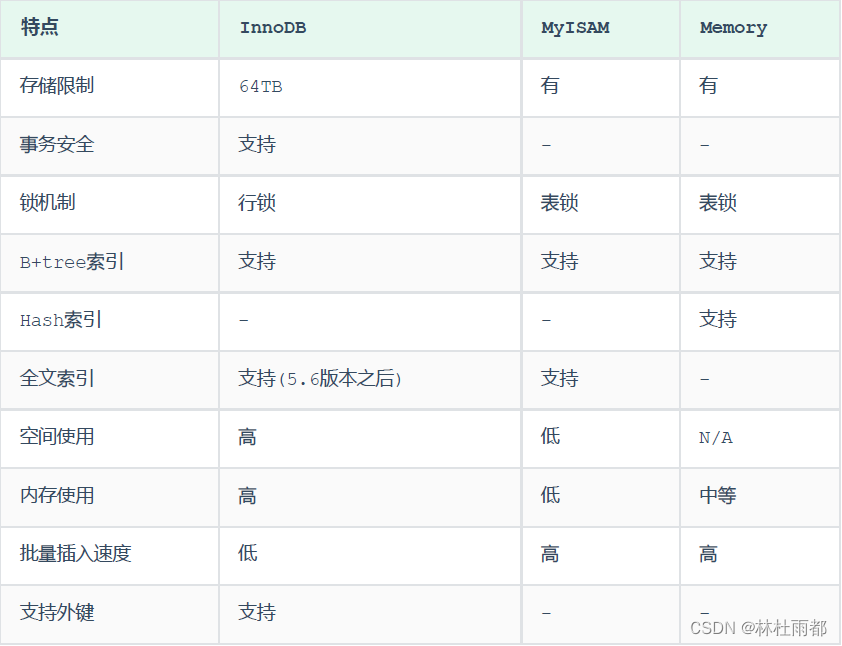
在介绍神经网络语言模型结构的时候，每个词 w 都对应一个长度为 m 的向量 C(w)，这些向量拼接在一起构成了神经网络语言模型的输入 x。但是并没有说如何得到 C(w)。

七、词向量

8. 遗留问题

• 如何获得 C(w)也是神经网络语言模型与普通全连接神经网络不一样的地方。开始训练时 C(w)的值是随机设置的，在训练过程中，同神经网络的权重一样，C(w)也一同被训练，把它当作参数看待就可以了。当训练结束时，每个词都得到了一个向量，这个向量就是该词的一种表示，所以这个向量又称作词向量。

• 以前说的训练都是指训练神经网络的权重，BP 算法也是这么推导出来的，而 C(w)是神经网络的输入，怎么训练呢？

• C(w)虽然是神经网络的输入，但是也可以像权重那样进行训练，道理是一样的。

9. 如何训练词向量

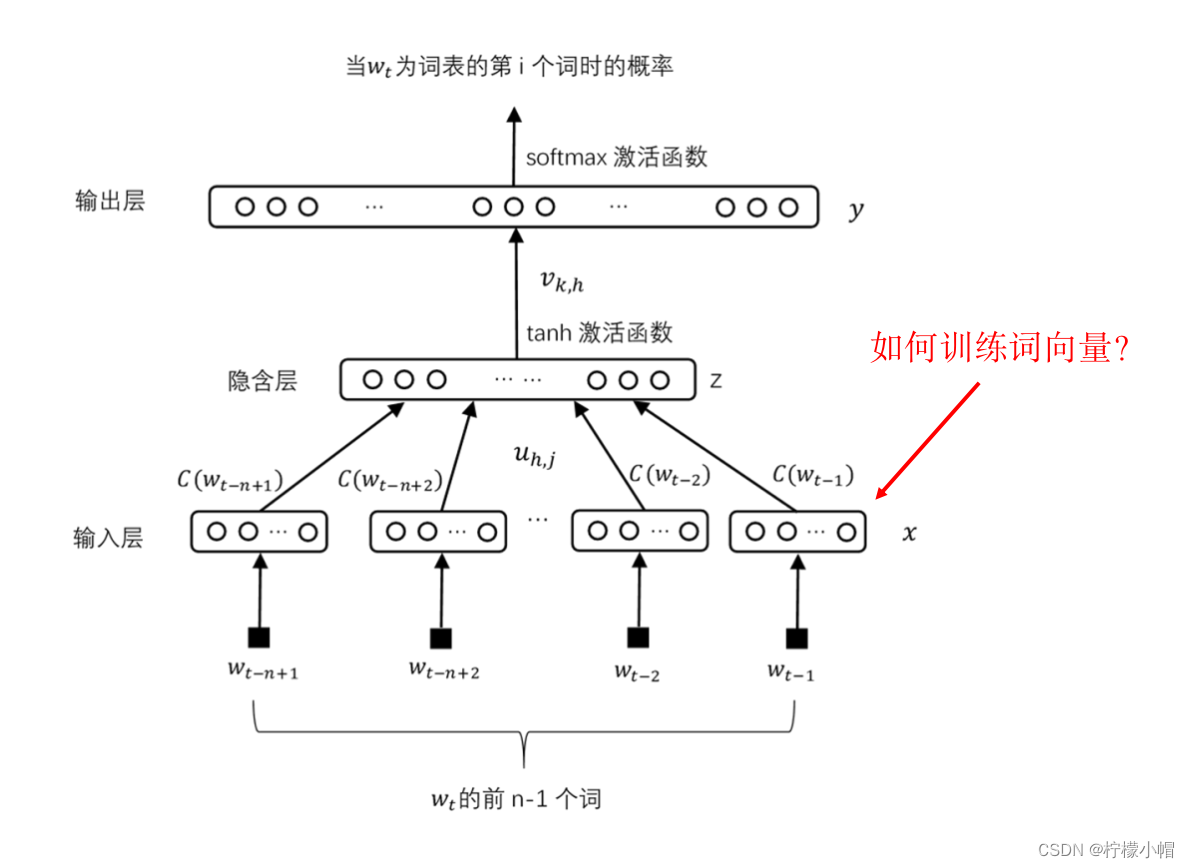
• 下图左边是个简单的神经网络，$x_1$ 、$x_2$ 、$x_3$ 是输入，$w_1$ 、$w_2$ 、$w_3$ 是权重。我们像下图右边那样，在下边增加一个只含有一个输入的输入层，输入恒定为1，中间三个原来的输入看做是隐含层的神经元，而将 $x_1$ 、$x_2$ 、$x_3$ 看做是输入层到隐含层的三个权重。这样右边的神经网络与左边的神经网络是完全等价的。所以， $x_1$ 、$x_2$ 、$x_3$ 这三个原来的输入，就可以当作权重，像权重一样训练了。

• 通过这样的方法，我们就可以得到词的稠密表示——词向量了。

10. 词向量（词嵌入）的性质

• 一般来说，语义相近的词，其上下文也往往会比较相一致，比方说“计算机”、“电脑”两个词，几乎可以任意互换，这样语义近似的词得到的词向量也会比较接近，就可以通过计算两个词向量的距离等方式“计算”两个词的语义相似性。这样得到的词向量还可以进行向量运算，满足一些向量的性质。
  
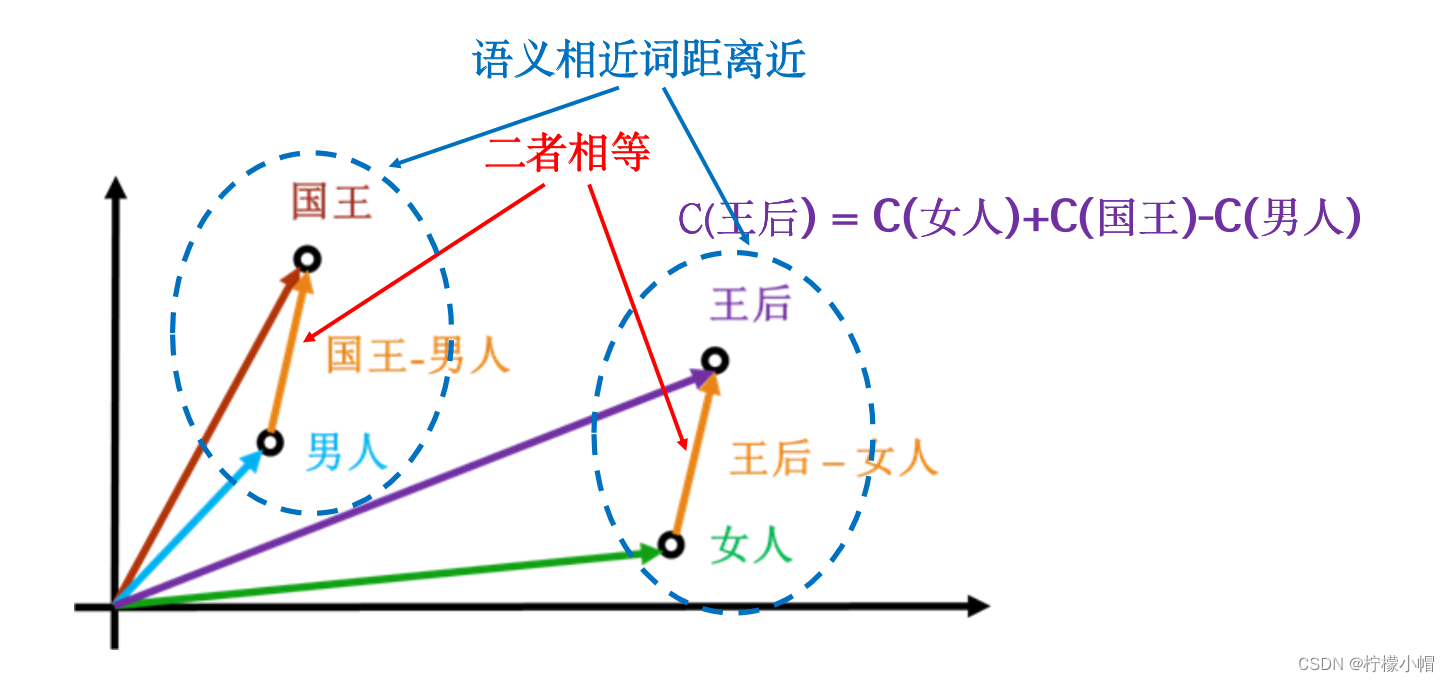
• 如图所示，给出了“国王”、“王后”、“男人”、“女人”4个词的词向量示意图。“国王”相对于“男人”的关系，可以等同地看做“王后”与“女人”的关系，所以：
  • C(国王)-C(男人) = C(王后)-C(女人)
• 其中C(w)表示词w的词向量，符号“-”表示向量减法，下面用的到符号“+”也是指向量加法。这样，如果假设我们不知道“王后”的词向量，就可以利用向量运算计算得到：
  • C(王后) = C(女人)+C(国王)-C(男人)
• 这些都体现了这种词向量表示的优越性，也体现了这样得到的词向量确实能够体现出词义信息。
• 但是这个神经网络语言模型有个不足，就是计算起来太慢了。

11. NNLM 存在的问题

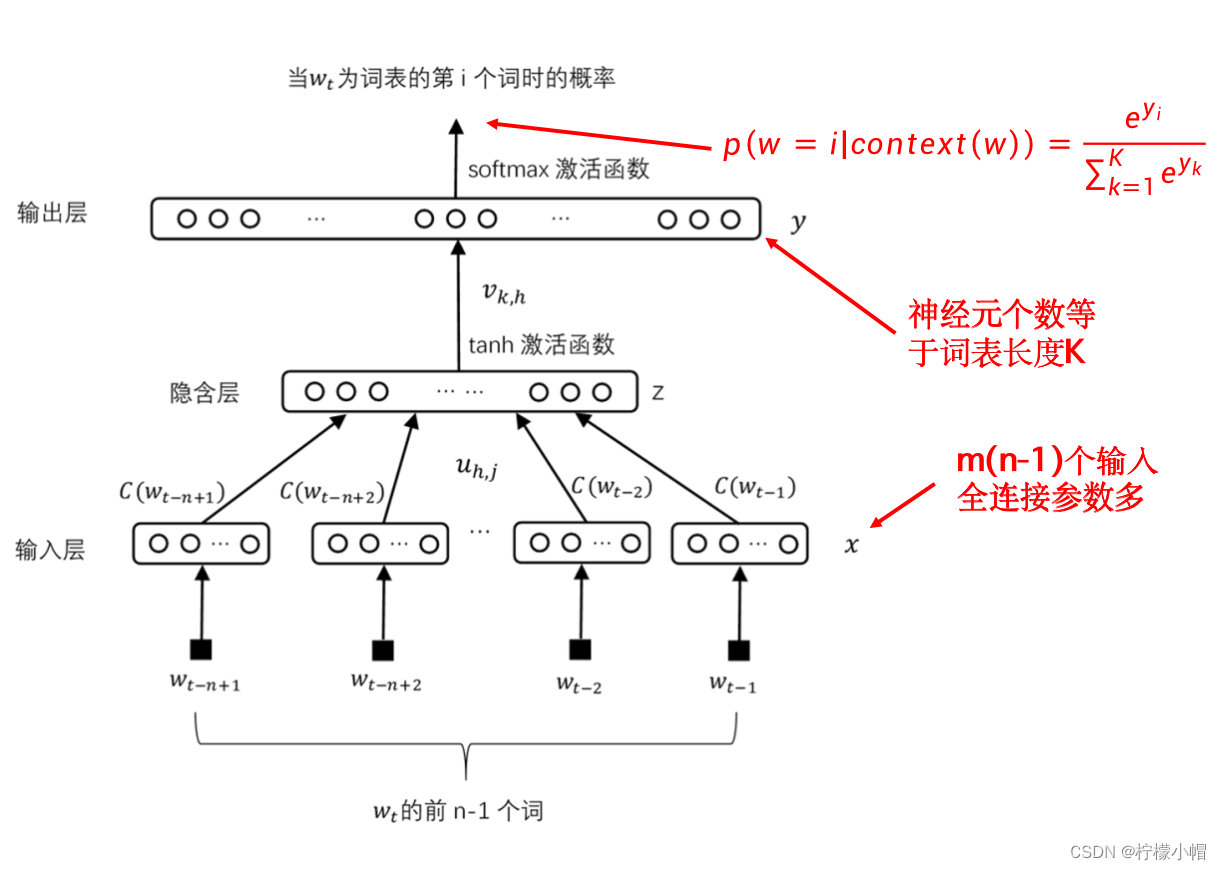
• 常用词一般会有几十万个，每个词均对应一个神经网络的输出，又由于采用了softmax激活函数，每次计算softmax需要用到所有的输出值。
• 计算softmax时分母部分要对所有输出计算e^(y_k )，再求和，运算量很大，会影响速度。
  

12. word2vec 模型（CBOW）

• 为此提出了一种称作word2vec的简化模型，如图所示。word2vec模型有两种实现方式，其中的一种，称作连续词袋模型（CBOW）。
  
  
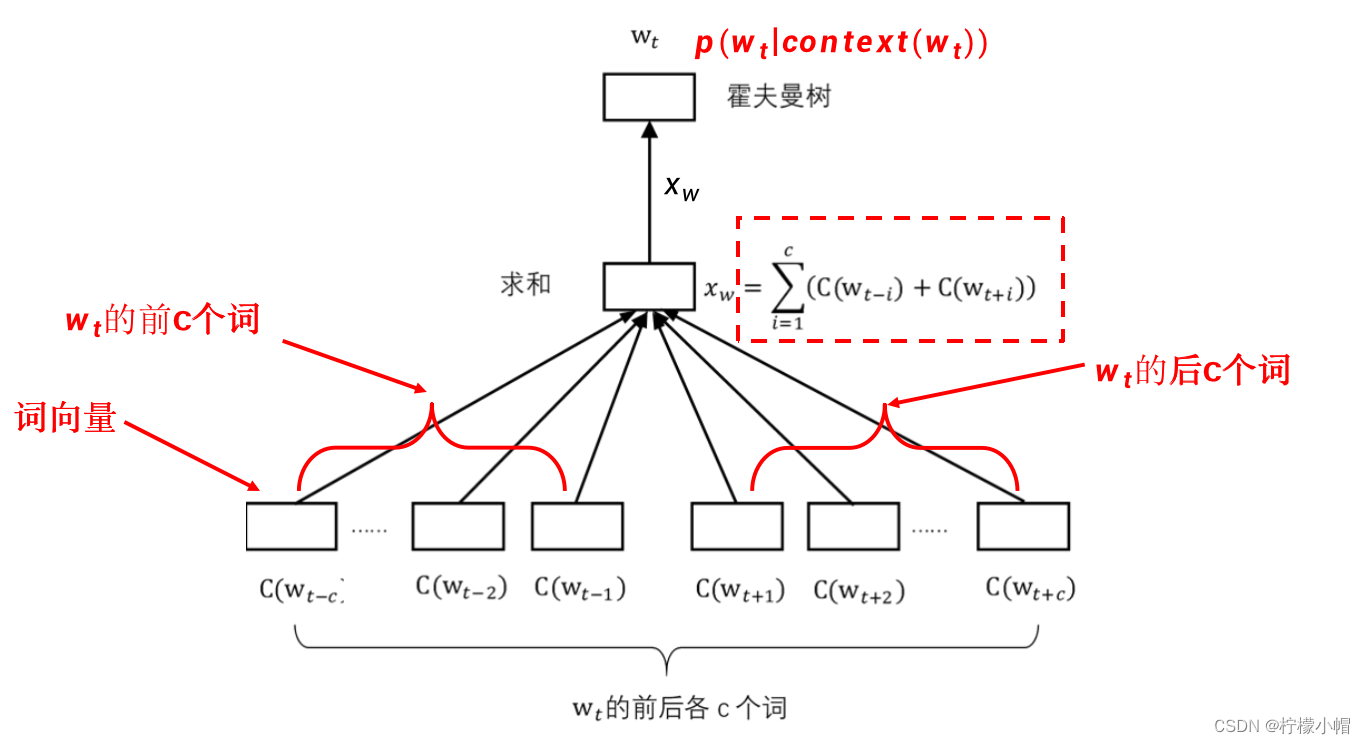
• 在这个模型中，输入的上下文不是当前词的前n-1个词，而是当前词 $w_t$的前c个词 $w_{t-c},\cdots ,w_{t-1}$ 和后c个词 $w_{t+1},\cdots w_{t+c}$ ，窗口大小为2c。同样，上下文中的每个词对应一个长度为m的向量 $C(w_i)$ ，共有2c个。 $C(w_i)$ 的含义与前面介绍的神经网络语言模型一样，是对应词的词向量。中间层的构成是将这2c个向量按位相加在一起，构成向量 $x_w$ ，该向量的长度同样为m，而不是像前面介绍的神经网络语言模型那样将词向量拼接在一起，减少了神经网络的参数量。该模型的输出同样是在给定上下文环境下某个词 $w_t$ 的概率，但是为了避免计算softmax以提高计算速度，采用了一种称作层次softmax的方法近似softmax的效果。

13. 霍夫曼树与霍夫曼编码

13.1 什么是霍夫曼树？

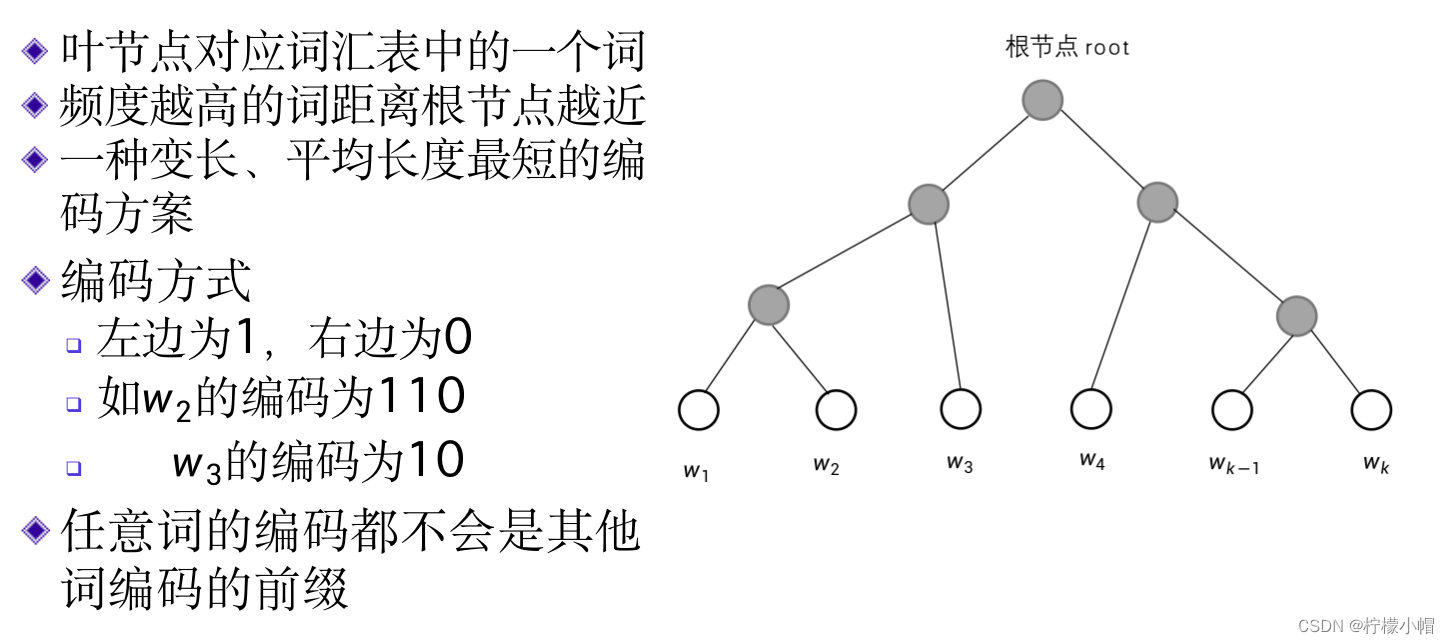
• 下图所示，是一个词表的霍夫曼树示意图，最上边的实心圆为树的根节点root，下边的空心圆为叶节点，每个叶节点对应词表中的一个词，词表有多大，就有多少个叶节点。霍夫曼树是一个二叉树，也就是说，每个节点最多可以有两个子节点。从霍夫曼树可以得到词表中每个词的唯一编码。

13.2 如何从霍夫曼树得到词的编码呢？

• 从根节点root到任何叶节点都存在一条路径，从root开始向下，每遇到一个节点需要选择向左还是向右，最终可以到达某个叶节点。从root开始，选择“左左右”就到达了 $w_2$ ，选择“左右”就到达了 $w_3$ 。如果“左”用“1”表示，“右”用“0”表示，就可以得到一个词的编码，比如 $w_2$ 的编码为“110”，$w_3$ 的编码为“10”等。这就是词的霍夫曼编码。这种编码的特点是不等长，霍夫曼树可以根据每个词的使用频度产生，可以使得常用词的编码短，非常用词的编码长，而且任何一个短的编码都不会是另一个长的编码的前一部分，比如“10”是 $w_3$ 的编码，则除了 $w_3$ 以外，不可能还有其他词的编码是以“10”开始的。所以，如果用霍夫曼编码表示一篇文章的话，词的编码之间不需要空格等分隔符，就可以区分出来。比如“10110”只能拆分为“10”、“110”，而不可能有其他的拆分结果。由于越是常用词其编码越短，所以霍夫曼编码也是一种平均编码长度最短的编码方法。

14. 对比

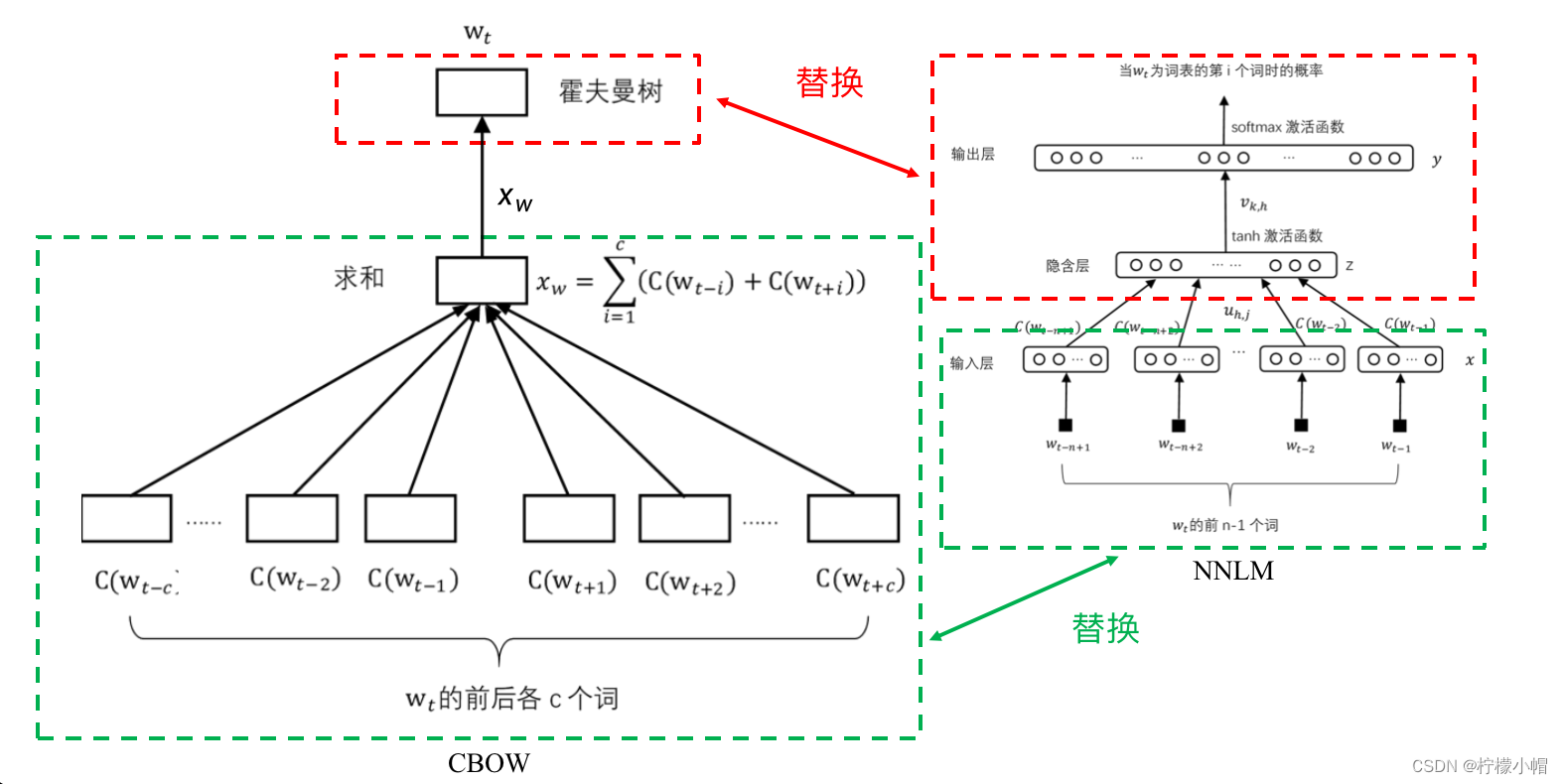
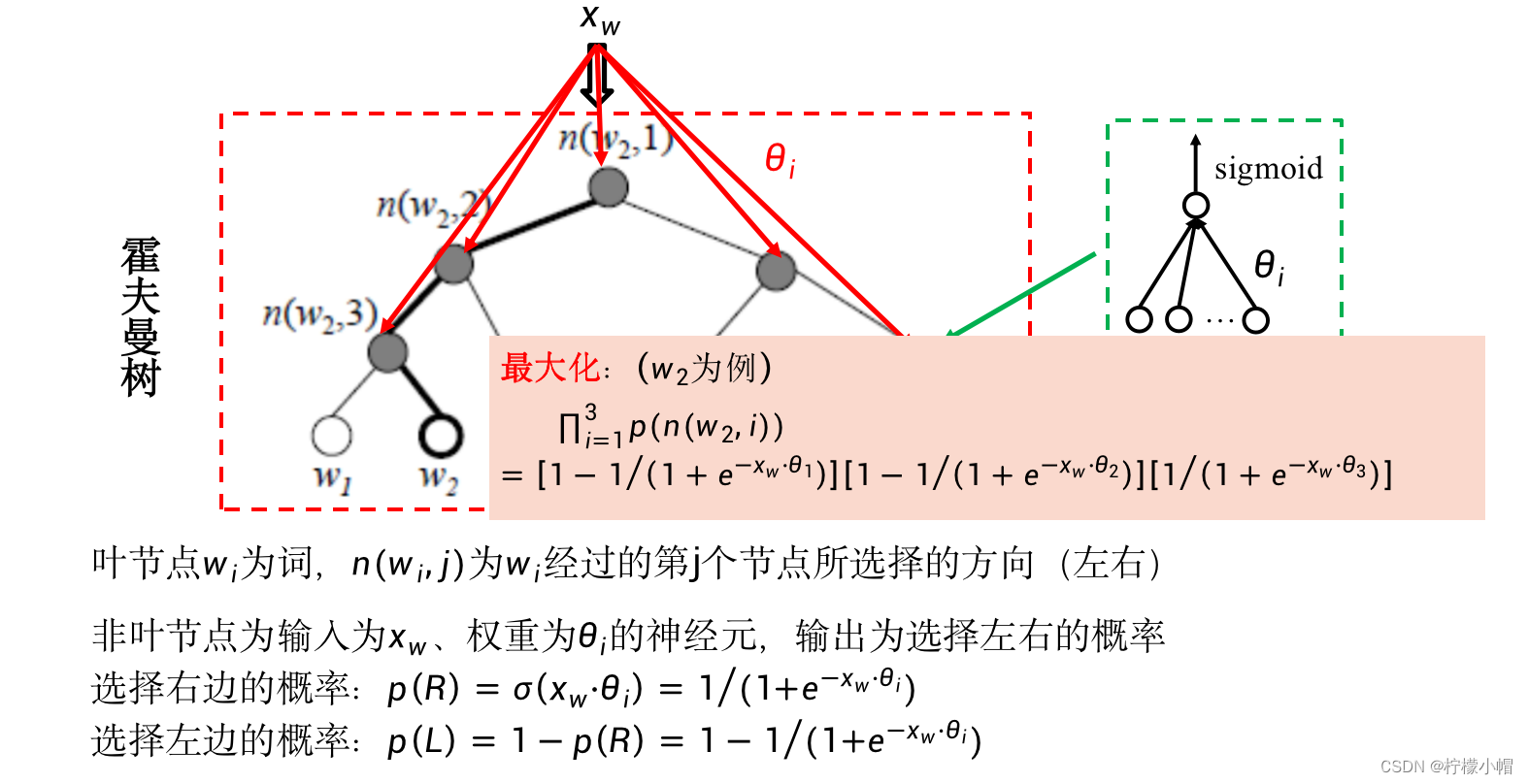
• 在上图中，词 $w_t$ 的上下文对应的词向量经求和后得到 $x_w$ 。霍夫曼树的每一个非叶节点，也就是图中的灰色节点，都单独看做是一个神经元，输入是 $x_w$ ，输出是一个概率值，表示到达这个节点后向右走的概率 $p(R)$ ，那么向左走的概率就是 $p(L)=1-p(R)$ 。这样的话，任何一个词w依据其霍夫曼编码就可以得到一个从root到达该词的概率。比如对于词 $w_2$ 其霍夫曼编码为“110”，从root开始，第一个节点应该向左走，其概率为 $p_1(L)$ ，第二个节点还是向左走，其概率为 $p_2(L)$ ，第三个节点是向右走，其概率为 $p_3(R)$ 。这样，从root到达 $w_2$ 的概率就应该是三个概率的乘积，即：
  $$p_1(L)\cdot p_2(L)\cdot p_3(R)=(1-p_1(R))\cdot (1-p_2(R))\cdot p_3(R)$$
• 在训练的时候，对于词表中的每一个词，也就是霍夫曼树的任何一个叶节点，都对应着这样的概率，训练目标就是使该概率值最大。同前面讲的神经网络语言模型一样，我们也同样通过求对数再加负号的办法，将该最大值问题转化为最小值问题，并以此作为损失函数，以便可以用BP算法求解。比如对于词 $w_2$ 来说，其损失函数就是：
  $$-(log(1-p_1(R))+log(1-p_2(R))+log{p}_3(R))$$
• 概率 $p(R)$ 、$p(L)$ 如何计算呢？
• 霍夫曼树的每个非叶节点都看做是一个神经元，注意不是神经网络，就是一个单独的神经元，每个神经元的输入都是一样的，均为 $x_w=[x_1,x_2,...,x_m]$ ，但是每个神经元有各自的参数即权重w，最后再加一个sigmoid激活函数，神经元的输出就是向右走的概率，而用1减去向右走的概率就是向左走的概率。
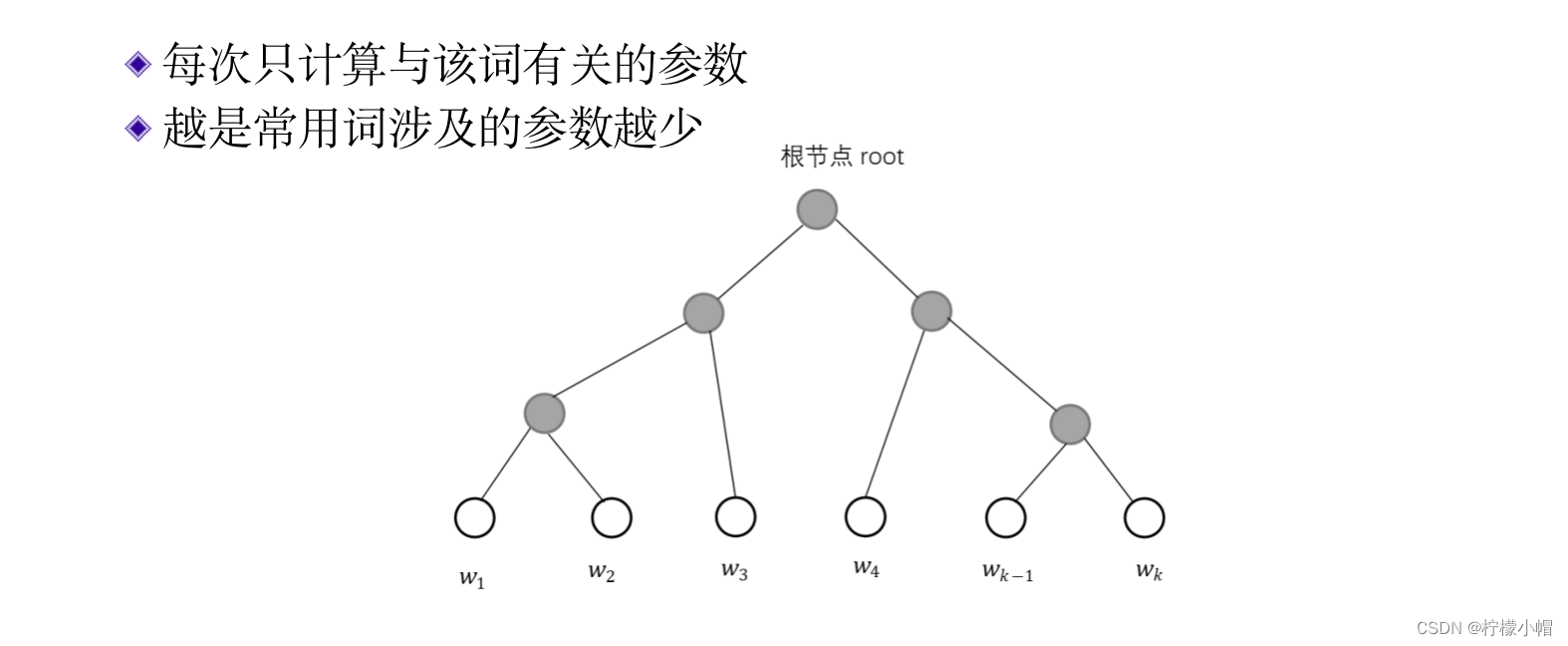
• 这样做的好处是，每次训练一个词时只需修改与本词相关的参数，不涉及其他参数，不像前面讲过的神经网络语言模型那样计算softmax时，要计算所有词的概率值，从而提高了训练速度。同时由于使用了霍夫曼编码，常用词的编码短，涉及到的神经元就少，从而进一步提高了计算速度。

15. 一般性描述

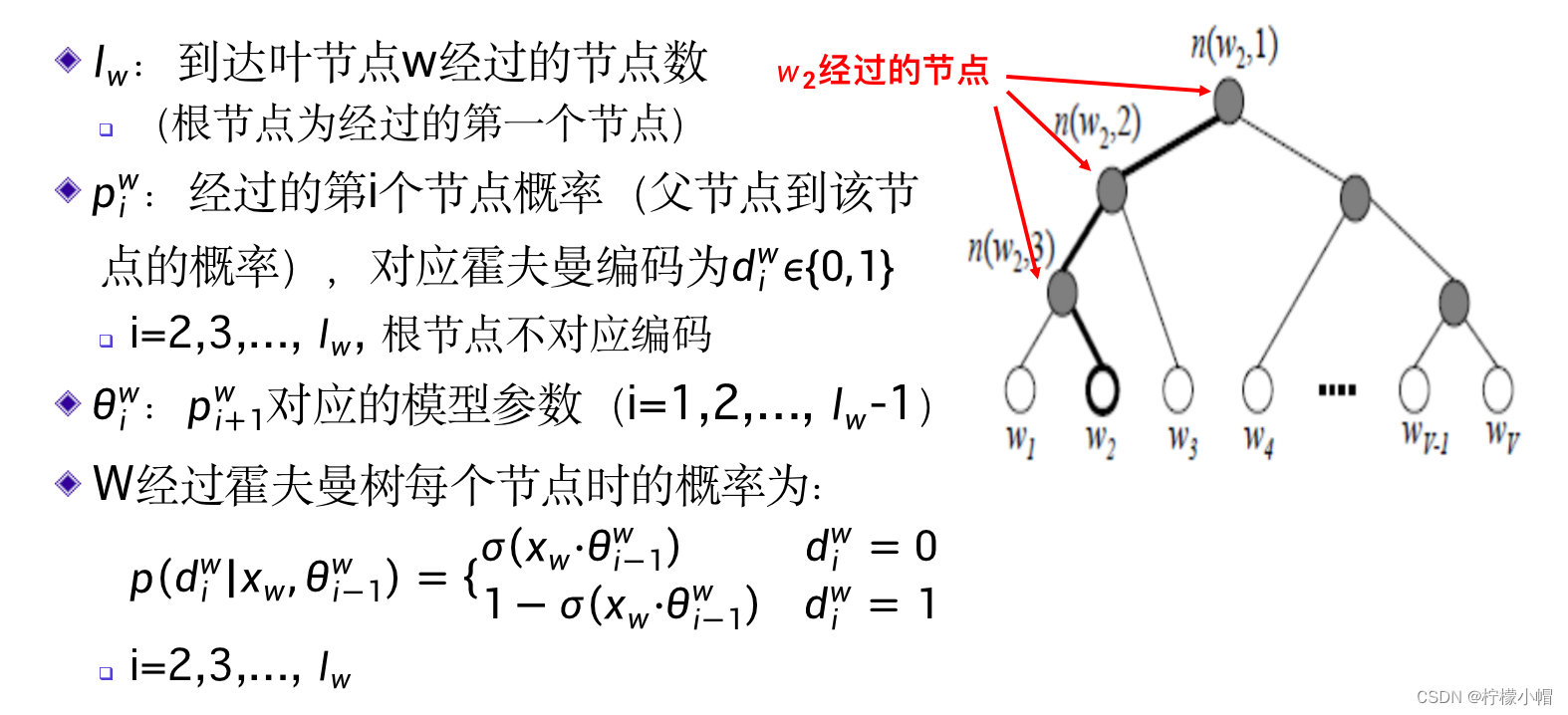
16. 获得词向量

• 这也是一种神经网络语言模型，作为词向量的输入也同前面讲过的神经网络语言模型一样，通过训练得到。以上就是word2vec模型的实现方法之一：连续词袋模型（CBOW）。
  

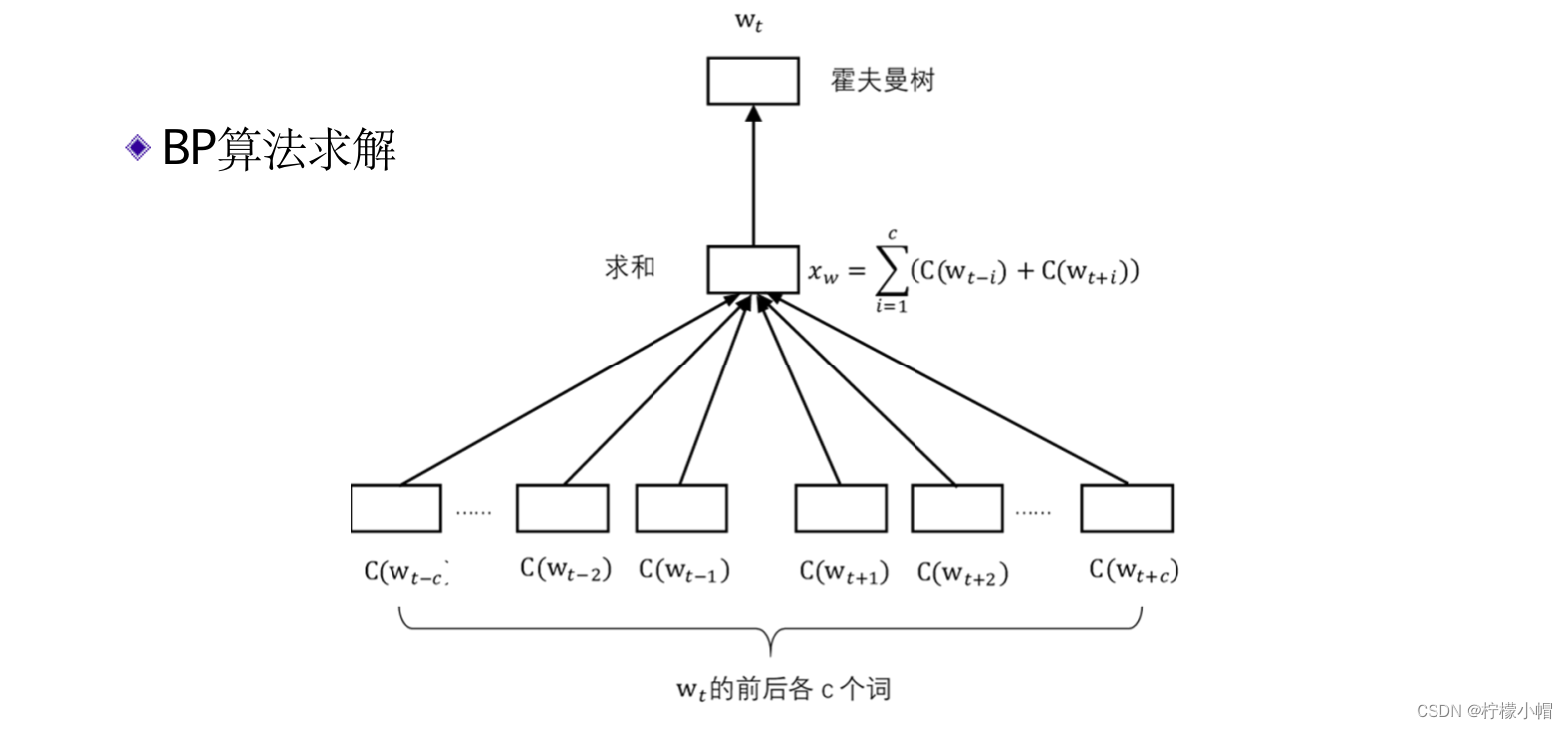
17. 训练计算量

18. word2vec 模型（跳词模型）

• word2vec 模型除了连续词袋模型外，还有一种模型称作 Skip-Gram。
• 对于连续词袋模型来说，是通过词 w 两侧的上下文预测 w 出现的概率，而 Skip-Gram 模型刚好相反，是通过词 w 预测它两侧出现哪些词的概率。
• 总之，我们通过训练神经网络语言模型的办法，可以获得词的向量表示，有了这种向量表示后，就可以用神经网络进行文本处理了。

19. 词向量应用举例：TextCNN

• 情感分类
  • 比如说刚看完一部电影，你说：“我很喜欢这部电影”，这就体现了正的情感，如果说的是：“这部电影不好看”，体现的就是负的情感。把一句具有感情色彩的话分成正的情感或者负的情感，就是情感分类问题。
• 下图给出了一个用于情感分类的神经网络示意图，该模型被称作 TextCNN，Text 就是文本的意思，而 CNN 则是卷积神经网络的英文缩写。下面我们仔细解释一下这个神经网络。首先说明一下，这只是个示意图，只是为了举例用，图中的一些超参数（人为设定的参数，如卷积核的个数、词向量长度等均属于超参数）并不是真实的数值，比如词向量长度图中设定为 5，实际系统中词向量长度可能有 300、400。
• 该神经网络的输入是一句话，图中示例的是“我 非常 喜欢 这部 城市 题材 电影”，共 7 个词组成。假定事先训练好了长度为 5 的词向量，依次取出句中每个词的词向量，一个词向量占一行从上到下排列，这样就得到了一个 7 行 5 列的句子矩阵。

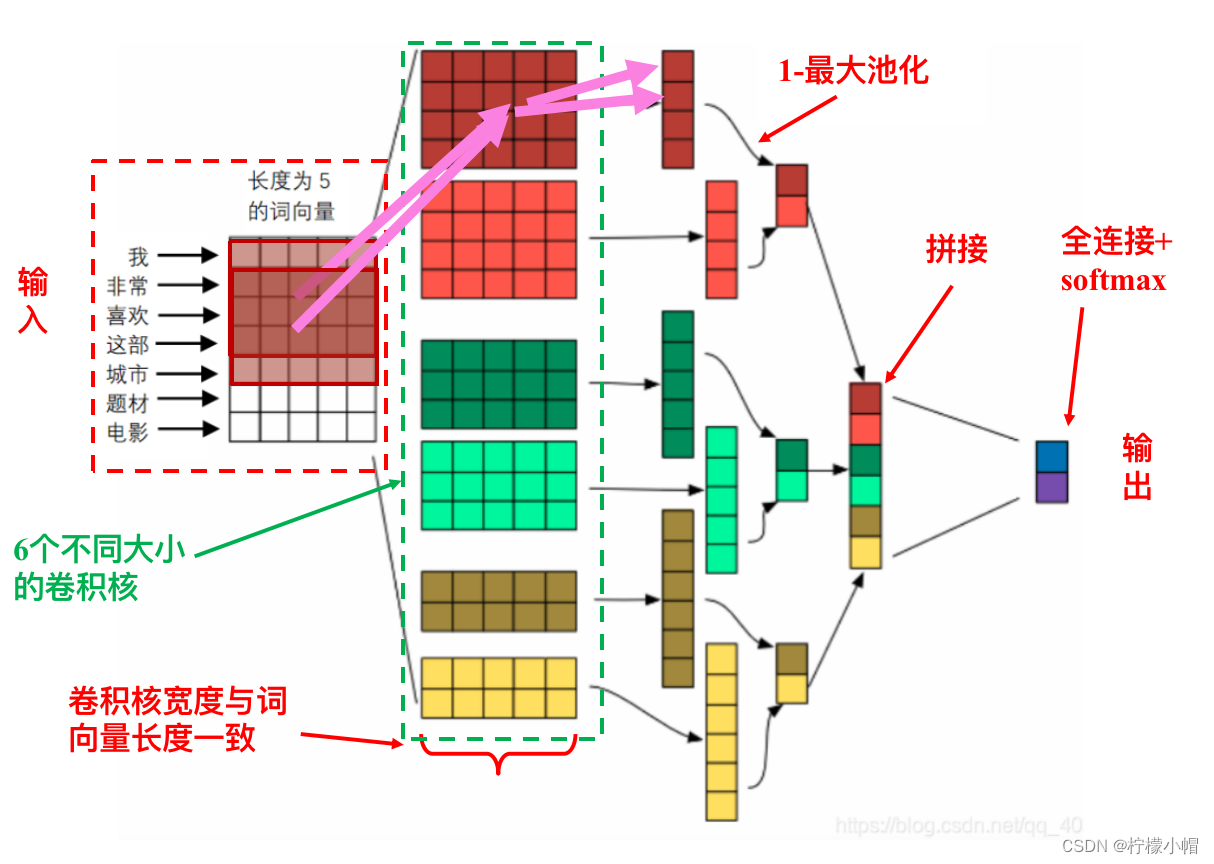
• 这个句子矩阵看起来跟一幅“图像”没啥区别，就可以像处理图像那样对句子用神经网络处理了。
• 但是有个问题。在处理图像时，卷积核都是“方”的，大小是 3×3、5×5 等，但是对于文本来说，由于每行对应一个独立的词，一个词向量不好从中间断开处理，所以在做卷积的时候需要有些变化，以便适应这个情况。
• 对于 3×3、5×5 这样的卷积核，我们称为二维卷积，对于文本来说，我们要用到一维卷积。也就是说，卷积核的宽度默认与词向量的长度一致，我们只规定卷积核的高度，而卷积核按照给定的步长，只在纵向移动，其他的与前面讲的卷积运算是一样的。

20. 文本卷积计算举例

• 在该图中输入是一个 4×5 的句子矩阵，词向量长度为 5，卷积核的大小为 3，即卷积核的高为 3，宽与词向量长度一致为 5。卷积得到两个结果，一个是卷积核与句子矩阵上面 3 行的卷积结果为-8，见图上半部分。然后按照卷积步长为 1，向下移动一行后，得到卷积的第二个结果，即句子矩阵后 3 行与卷积核的卷积结果为-7，见图下半部分。这里只是为了示意如何做一维卷积，卷积结果没有连接激活函数，实际系统中一般要连接激活函数。
• 在处理图像时，卷积核要先行后列对图像进行扫描，用的是二维卷积。但是在处理文本时，由于一行与一个词向量对应，不能将词向量断开处理，所以采用一维卷积进行处理，只沿着纵向扫描。
• 这就是文本卷积与图像卷积的不同之处。其他的都是一样的，比如多个卷积核就可以得到多个通道，对于多通道卷积，卷积核也有“厚度”，其厚度值与输入的通道数一致，这些也都是默认的。

• 弄清楚了一维卷积运算之后，TextCNN 的图的其他部分就不难懂了。在这个神经网络中，输入层直接连了一个卷积层，共有 6 个不同大小的卷积核，大小分别为 2、3、4，每种各两个，共获得 6 个通道。卷积时没有加填充，所以不同大小的卷积核得到的通道大小也不一样，分别为 6、5、4。然后对每个通道做一次 1-最大池化，也就是每个通道中选取一个最大值作为池化的结果，再把这 6 个结果拼接成一个长度为 6 的向量，向量的每个元素可以看做是一个神经元，再与输出层的两个神经元做全连接，最后通过 softmax 输出。输出层的两个神经元分别代表输入句子具有正情感或负情感的概率。这样就可以实现对句子情感的两级分类。
• 如果是在训练阶段，则需要标注好大量的情感句子，利用这些标注好的样本，采用 BP 算法训练神经网络。
• 有了词向量表示之后，用神经网络处理句子跟处理图像没有太大的差别，除了个别地方需要考虑句子特点外，其他的地方都差不多。
• 在这个神经网络中用到了 1-最大池化，同时也可以用其他的最大池化方法，比如在最大池化时可以从一个通道中选取两个或者更多的元素，也可以把通道分成若干部分，每部分取最大的，等等。
• 当固定了卷积核的大小后，对于不同长度的文本，卷积后结果的大小是不一样的，在 TextCNN 中，由于采用了 1-最大池化，无论句子长短，一个通道最后都得到了一个最大的结果，所以从某种角度来说，这种方法也是可以处理不同长短的文本的，但是文本长度也不能变化太大。

21. 总结

• 要用计算机处理自然语言，首先遇到的一个问题如何表达一个词，以便让计算机能够处理。“独热”是一种简单的词的表示方法，该方法用一个与词表等长的向量表示一个词，在词表的对应位为 1，其余位置为 0。比如某词在词表中处于 123 的位置，则独热表示法就是一个向量，只在向量的第 123 位为 1，其他位置都是 0。这是一种非常稀疏的表示方法，优点是简单，缺点有很多，比如向量太长、不能根据词的表示计算词间相似性等。

• 与独热表示法相对应的是词的稠密表示法，一个词也是表示为一个向量，但是向量长度一般是几百维，不需要词表那么长。另外就是表示词的向量，几乎每一位都不为 0，而是向量的每一位都参与到词的表示中，所以这种方法又称为词的分布式表示。

• 词用向量表示又称为词向量。词向量可以通过神经网络语言模型得到。所谓神经网络语言模型，就是在给定输入上下文下，下一个词是哪个词的概率。通过训练神经网络语言模型，可以获得词向量。神经网络语言模型同样通过 BP 算法进行训练，与普通的神经网络训练过程不同的是，在修改权重的同时，还要同时对输入进行修改。对输入的修改可以等价成对权重的修改，二者并没有本质的不同。最终在神经网络训练结束后，在输入层就得到了词向量。

• 为了解决神经网络语言模型训练速度慢的问题，提出了 word2vec 网络模型，与霍夫曼编码方法相结合，可以加快语言模型的训练过程。