目录
1 数组(Array)
1.1 定义和特点
1.2 基本操作
1.3 数组的时间复杂度
1.4 应用场景
2 链表(Linked List)
2.1 定义和特点:
2.1.1 单向链表(Singly Linked List)
2.1.2 双向链表(Doubly Linked List):
2.1.3 循环链表(Circular Linked List):
2.2 基本操作
2.2.1 创建链表:
2.2.2 插入节点:
2.2.3 删除节点
2.2.4 遍历链表
2.3 时间复杂度
2.4 应用场景
1 数组(Array)
- 数组是一种线性数据结构,由相同类型的元素组成,每个元素通过索引来访问。
- 元素在内存中是连续存储的。
- 数组的大小通常在创建时固定,不易扩展或缩小。
1.1 定义和特点
示例:
# 创建一个整数数组,包含5个元素
my_array = [10, 20, 30, 40, 50]
# 访问数组中的元素,通过索引访问
print(my_array[0]) # 输出:10
print(my_array[3]) # 输出:40
# 修改数组中的元素
my_array[2] = 35
# 遍历数组并打印所有元素
for element in my_array:
print(element)
# 输出:
# 10
# 20
# 35
# 40
# 50
数组(Array)是一种常见的线性数据结构,它包含相同类型的元素,并且每个元素都可以通过索引来访问。数组中的元素在内存中是连续存储的,这意味着它们的地址是连续的,这有助于快速的元素访问。数组的大小通常在创建时固定,不易扩展或缩小,这是数组与其他动态数据结构(如动态数组或链表)的主要区别。
在示例中,我们创建了一个包含5个整数元素的数组,并使用索引来访问和修改元素。数组中的元素在内存中是连续存储的,这样我们可以高效地访问它们。请注意,数组的大小在创建时固定,如果需要更多的元素,需要创建一个新的数组。
1.2 基本操作
- 创建数组:声明数组类型和大小。
- 访问元素:使用索引访问特定位置的元素。
- 插入元素:将新元素插入到数组的指定位置。
- 删除元素:从数组中删除指定位置的元素。
- 更新元素:修改数组中特定位置的元素值。
创建数组:
- 创建数组时,通常需要声明数组的类型和大小。不同编程语言可能有不同的语法来创建数组。
- 数组的大小表示数组可以容纳多少个元素,一旦大小固定,通常不能轻松改变。
my_array = [0, 0, 0, 0, 0] # 创建一个包含5个元素的整数数组访问元素:
可以使用数组的索引来访问特定位置的元素。索引通常从0开始递增,表示元素在数组中的位置。
value = my_array[2] # 访问索引为2的元素,将值赋给变量value插入元素:
在数组中插入元素通常需要指定要插入的位置和要插入的值。插入操作可能需要移动后面的元素以腾出空间。
my_array.insert(2, 25) # 在索引为2的位置插入值25删除元素:
从数组中删除元素通常需要指定要删除的位置。删除操作可能需要移动后面的元素以填补空白。
del my_array[3] # 删除索引为3的元素更新元素:
更新数组中的元素值只需通过索引访问元素并将新值分配给该元素。
my_array[1] = 15 # 更新索引为1的元素值为15这些操作是数组的常见操作,但请注意,数组的性质取决于编程语言和库的实现。在某些语言中,数组可能是固定大小的,而在其他语言中,可能存在动态数组,它们可以自动扩展以容纳更多元素。确保了解所使用的编程语言或库中数组的行为和限制。
# 创建一个整数数组
my_array = [1, 2, 3, 4, 5]
# 访问数组元素
first_element = my_array[0] # 第一个元素
second_element = my_array[1] # 第二个元素
# 修改数组元素
my_array[2] = 10 # 将第三个元素修改为10
# 获取数组的长度
array_length = len(my_array) # 返回数组的长度,这里为5
# 插入元素(在索引位置2插入新元素)
my_array.insert(2, 6) # [1, 2, 6, 10, 4, 5]
# 删除元素(删除第四个元素)
del my_array[3] # [1, 2, 6, 4, 5]
1.3 数组的时间复杂度
- 访问元素:O(1)
- 插入和删除元素(在特定位置):O(n)
- 更新元素:O(1)
访问元素:O(1)
访问数组中特定索引位置的元素的时间复杂度是常数时间,因为可以通过索引直接计算元素的内存地址。
my_array = [1, 2, 3, 4, 5]
element = my_array[2] # 访问索引为2的元素(值为3),时间复杂度为O(1)插入和删除元素(在特定位置):O(n)
- 插入和删除数组中特定位置的元素需要将该位置之后的元素都向后移动或向前移动,以便为新元素或填充元素腾出空间。因此,这些操作的时间复杂度是线性的,与数组长度相关。
示例
my_array = [1, 2, 3, 4, 5]
my_array.insert(2, 6) # 在索引2处插入元素6,需要将后面的元素移动,时间复杂度为O(n)
del my_array[3] # 删除索引3处的元素,需要将后面的元素移动,时间复杂度为O(n)
更新元素:O(1)
- 更新数组中特定索引位置的元素的时间复杂度是常数时间,因为只需找到索引并修改该位置的值。
示例:
my_array = [1, 2, 3, 4, 5]
my_array[2] = 10 # 更新索引2处的元素为10,时间复杂度为O(1)
需要注意的是,虽然插入和删除元素的时间复杂度为O(n),但在某些情况下,如果操作是在数组末尾进行的,实际上可能只需常数时间。但在最坏情况下,需要移动大量元素,因此平均时间复杂度为O(n)。
总结:数组的时间复杂度取决于具体的操作,访问元素的操作非常高效(O(1)),但插入和删除元素的操作通常较慢(O(n)),更新元素的操作也非常高效(O(1))。因此,在选择数据结构时,需要根据不同的操作需求权衡数组的优缺点。
1.4 应用场景
- 适用于需要快速访问元素和已知大小的情况。
- 数组用于实现各种数据结构,如栈、队列和矩阵等。
数组在以下情况下非常适用:
-
快速访问元素:由于数组中的元素在内存中是连续存储的,因此可以通过索引非常快速地访问特定位置的元素。这使得数组非常适合需要频繁访问元素的应用。
-
已知大小:数组的大小通常在创建时固定,不易扩展或缩小。因此,当知道数据集的大小是固定的或可以提前确定时,使用数组是一个不错的选择。
-
实现其他数据结构:数组可以用于实现各种其他数据结构,如栈、队列、矩阵等。例如,栈可以通过数组的末尾进行操作,队列可以通过数组的前端进行操作,矩阵可以使用多维数组表示。
示例1:使用数组实现栈
class Stack:
def __init__(self):
self.items = []
def push(self, item):
self.items.append(item)
def pop(self):
if not self.is_empty():
return self.items.pop()
def is_empty(self):
return len(self.items) == 0
def peek(self):
if not self.is_empty():
return self.items[-1]
def size(self):
return len(self.items)
# 创建一个栈并进行操作
stack = Stack()
stack.push(1)
stack.push(2)
stack.push(3)
print(stack.pop()) # 输出: 3
print(stack.peek()) # 输出: 2
示例2:使用数组表示矩阵
# 创建一个3x3矩阵
matrix = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
# 访问矩阵中的元素
element = matrix[0][1] # 访问第一行第二列的元素,输出: 2
# 更新矩阵中的元素
matrix[1][2] = 10 # 更新第二行第三列的元素为10
# 输出整个矩阵
for row in matrix:
print(row)
# 输出:
# [1, 2, 3]
# [4, 5, 10]
# [7, 8, 9]
总之,数组在需要快速访问元素和已知大小的情况下非常有用,并且可以用于实现各种常见的数据结构和数据表示。
2 链表(Linked List)
2.1 定义和特点:
- 链表是一种线性数据结构,由节点组成,每个节点包含数据和指向下一个节点的指针。
- 链表中的节点在内存中不一定是连续存储的,它们通过指针连接在一起。
- 链表可以具有不同的类型,如单向链表、双向链表和循环链表。
链表(Linked List)是一种常见的线性数据结构,与数组不同,链表中的元素(节点)不是在内存中连续存储的,而是通过指针相互连接在一起。每个节点包含两个部分:数据和指向下一个节点的指针。
主要的链表类型包括:
2.1.1 单向链表(Singly Linked List)
- 每个节点包含数据和一个指向下一个节点的指针。
- 最后一个节点的指针通常指向空(null)。

2.1.2 双向链表(Doubly Linked List):
- 每个节点包含数据、指向下一个节点的指针和指向前一个节点的指针。
- 可以在前后两个方向上遍历链表。

2.1.3 循环链表(Circular Linked List):
- 单向或双向链表的一个变种,最后一个节点指向第一个节点,形成一个循环。
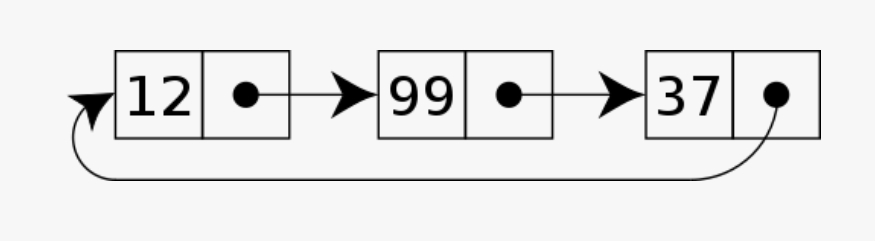
链表的优势在于可以在运行时动态分配内存,因此不需要像数组一样预先指定大小。
这使得链表在某些情况下更灵活,但也导致了访问元素的效率较低,因为需要按顺序遍历链表。
示例(Python中的单向链表):
class Node:
def __init__(self, data):
self.data = data
self.next = None # 初始时没有下一个节点
# 创建链表
node1 = Node(10)
node2 = Node(20)
node3 = Node(30)
# 连接节点
node1.next = node2
node2.next = node3
# 遍历链表并打印数据
current_node = node1
while current_node is not None:
print(current_node.data)
current_node = current_node.next
这是一个简单的单向链表示例,其中每个节点包含一个整数数据和指向下一个节点的指针。链表从node1开始,依次包含node2和node3,最后一个节点的指针为None。遍历链表时,我们从第一个节点开始,通过next指针移动到下一个节点,直到链表的末尾。
2.2 基本操作
- 创建链表:声明头节点并初始化为空。
- 插入节点:在链表中插入新节点,通常有头插法和尾插法。
- 删除节点:从链表中删除指定节点。
- 遍历链表:按顺序访问链表中的所有节点。
链表是一种基本的数据结构,它由节点组成,每个节点包含数据和指向下一个节点的指针。下面详细解释链表的基本操作,并附带示例。
2.2.1 创建链表:
链表的创建通常从声明头节点开始,初始时头节点为空。头节点是链表的入口,用于访问整个链表。
2.2.2 插入节点:
在链表中插入新节点有两种常见的方法:
- 头插法(Insert at the Beginning):将新节点插入到链表的开头,新节点成为新的头节点。
- 尾插法(Insert at the End):将新节点插入到链表的末尾。
2.2.3 删除节点
从链表中删除指定节点通常有以下步骤:
- 找到待删除节点的前一个节点(前驱节点)。
- 更新前驱节点的指针,将其指向待删除节点的下一个节点,从而绕过待删除节点。
2.2.4 遍历链表
遍历链表意味着按顺序访问链表中的所有节点,通常使用循环来实现。
下面是一个简单的示例,演示了如何创建、插入、删除和遍历链表:
# 定义链表节点类
class Node:
def __init__(self, data):
self.data = data
self.next = None
# 定义链表类
class LinkedList:
def __init__(self):
self.head = None
# 插入节点到链表末尾(尾插法)
def append(self, data):
new_node = Node(data)
if not self.head:
self.head = new_node
else:
current = self.head
while current.next:
current = current.next
current.next = new_node
# 删除节点
def delete(self, data):
if not self.head:
return
if self.head.data == data:
self.head = self.head.next
return
current = self.head
while current.next:
if current.next.data == data:
current.next = current.next.next
return
current = current.next
# 遍历链表并打印节点数据
def display(self):
current = self.head
while current:
print(current.data, end=" -> ")
current = current.next
print("None")
# 创建一个空链表
my_linked_list = LinkedList()
# 插入节点
my_linked_list.append(1)
my_linked_list.append(2)
my_linked_list.append(3)
# 遍历并显示链表
my_linked_list.display() # 输出: 1 -> 2 -> 3 -> None
# 删除节点
my_linked_list.delete(2)
# 再次遍历并显示链表
my_linked_list.display() # 输出: 1 -> 3 -> None
2.3 时间复杂度
- 访问节点:O(n)
- 插入和删除节点:O(1)(如果已知节点位置)或O(n)(如果需要查找位置)
链表是一种线性数据结构,其访问、插入和删除操作的时间复杂度取决于操作的位置以及是否已知节点的位置。下面详细解释链表的时间复杂度,并附带示例。
访问节点:
链表中的节点没有像数组那样通过索引直接访问,而是需要从头节点开始沿着指针逐个遍历节点,因此访问节点的时间复杂度为O(n),其中n是链表的长度。
插入节点:
插入节点的时间复杂度取决于插入位置:
- 如果已知要插入的位置,如链表的头部,那么插入节点的时间复杂度为O(1),因为只需要更新指针。
- 如果需要在链表中间或末尾插入节点,但不知道插入位置,那么需要先遍历链表找到插入位置,因此插入节点的时间复杂度为O(n)。
删除节点:删除节点的时间复杂度也取决于删除位置:
- 如果已知要删除的节点位置,如链表的头部,那么删除节点的时间复杂度为O(1),因为只需要更新指针。
- 如果需要删除链表中间或末尾的节点,但不知道删除位置,那么需要先遍历链表找到删除位置,因此删除节点的时间复杂度为O(n)。
下面是一个示例,演示了访问、插入和删除节点的操作以及它们的时间复杂度:
# 定义链表节点类
class Node:
def __init__(self, data):
self.data = data
self.next = None
# 定义链表类
class LinkedList:
def __init__(self):
self.head = None
# 插入节点到链表末尾(尾插法)
def append(self, data):
new_node = Node(data)
if not self.head:
self.head = new_node
else:
current = self.head
while current.next:
current = current.next
current.next = new_node
# 删除节点
def delete(self, data):
if not self.head:
return
if self.head.data == data:
self.head = self.head.next
return
current = self.head
while current.next:
if current.next.data == data:
current.next = current.next.next
return
current = current.next
# 访问节点(需要遍历链表)
def access(self, index):
current = self.head
count = 0
while current:
if count == index:
return current.data
current = current.next
count += 1
return None
# 创建一个空链表
my_linked_list = LinkedList()
# 插入节点
my_linked_list.append(1)
my_linked_list.append(2)
my_linked_list.append(3)
# 访问节点(通过索引访问第二个节点)
value = my_linked_list.access(1)
print("访问节点:", value) # 输出: 2
# 删除节点
my_linked_list.delete(2)
# 访问节点(通过索引访问第二个节点,此时已删除节点2)
value = my_linked_list.access(1)
print("访问节点:", value) # 输出: 3
2.4 应用场景
- 适用于需要频繁插入和删除节点的情况,或者在不知道数据量的情况下存储数据。
- 链表常用于实现栈、队列、哈希表、LRU缓存等数据结构。
- 特殊类型的链表,如双向链表,可用于双向遍历。
-
动态数组:
- 动态数组是基于数组的数据结构,可以自动扩展或缩小大小以容纳不同数量的元素。
- 动态数组通常用于需要灵活性和效率的场景,但可能需要更多内存。
-
循环数组:
- 循环数组是一种特殊的数组,可以循环访问其元素,通常用于环形缓冲区和循环队列。
-
链表的变种:
- 单向链表:每个节点有一个指向下一个节点的指针。
- 双向链表:每个节点有一个指向前一个节点和下一个节点的指针。
- 循环链表:尾节点指向头节点,形成一个闭环。
以上是数组和链表的基本知识大纲,它们是数据结构中的重要概念,对于理解和设计算法以及解决各种编程问题非常重要。在实际编程中,选择合适的数据结构取决于问题的需求和性能要求。