前言:
本实验使用遗传算法寻找3维函数的最大/最小值,并对基因位数,种群初始大小,每次死亡个数,适应度计算方式这些参数进行修改,对比结果。
初始代码如下:
import numpy as np
import matplotlib.pyplot as plt
import random
import time # 暂停用的,方便我录像,你们不需要
# 所用的函数
def Function(x_data, y_data):
"""
:param x_data: x数值
:param y_data: y数值
:return: 输出表达式计算出的z
"""
# 本来想找个能可视化捏函数,给表达式的方法,在matlab绘图中发现这个表达式长得不错,就直接用了。
return 3 * (1 - x_data) ** 2 * np.exp(-x_data ** 2 - (y_data + 1) ** 2) - 10 * (
x_data / 5 - x_data ** 3 - y_data ** 5) * np.exp(
-x_data ** 2 - y_data ** 2) - np.exp(-(x_data + 1) ** 2 - y_data ** 2)
def Get_Grid(): # 生成坐标网格
"""
:return: 返回Function的x,y,z
"""
# 生成坐标网格
x = np.linspace(-4, 4, 100) # 坐标轴是-3~3,100个均匀分布,为了个体不跑到图片外,修改至-4~4
y = np.linspace(-4, 4, 100)
x, y = np.meshgrid(x, y) # 按刚刚的坐标轴生成二维矩阵
z = np.array(Function(x, y)) # 调用生成函数,获得y值
return x, y, z
def Get_Random_gene(number, n): # 随机生成基因型
"""
:param number: 生成个数
:param n: x的总位数
:return: 生成的族群
"""
return np.random.randint(0, 2, size=(number, n + n))
def Plot_Draw_F(fig, x, y, z): # 绘图,重新绘制F的图像,返回引用
"""
:param fig: 窗口的引用
:param x:
:param y:
:param z:
:return: axes_3d,画布引用
"""
fig.clf()
axes_3d = fig.add_subplot(111, projection='3d')
cmap = plt.cm.viridis # 设定变色的颜色,可选项:viridis, plasma, inferno, magma, cividis 等
norm = plt.Normalize(vmin=-5, vmax=5) # 颜色变化范围,不设置就是按z轴最大最小,
img_f = axes_3d.plot_surface(x, y, z, rstride=1, cstride=1, alpha=0.75, cmap=cmap, norm=norm) # 绘制3D图
# 长得还是有点抽象,一会发一下三视图,就能知道函数大概形状了
# 添加颜色条
cbar = fig.colorbar(img_f, ax=axes_3d)
cbar.set_label('Color')
# 设置坐标轴范围和标签
axes_3d.set_xlim(-4, 4)
axes_3d.set_ylim(-4, 4)
axes_3d.set_zlim(-10, 10)
axes_3d.set_xlabel('X')
axes_3d.set_ylabel('Y')
axes_3d.set_zlabel('Z')
return axes_3d
def Plot_Scatter(ax, plot_gene_data, plot_z, colour): # 根据解码后数据绘制种群的散点图
"""
:param ax: 画布引用
:param plot_z: 计算出的z值
:param plot_gene_data: 全部基因型转码后的数据
"""
for i in range(len(plot_z)):
ax.scatter(plot_gene_data[i][0], plot_gene_data[i][1], plot_z[i], c=colour, marker='o')
# 刷新图形
plt.draw()
plt.pause(1e-3)
# 解码,将全部二进制基因型数据转换为数值
def Decoding(data, n, point): # 输入的分别是要解码的列表,x,y,的位数,小数位数
"""
:param data: 要解码的列表,[[x符号,x整数部分,x整数部分,x整数部分,x小数部分,x小数部分,······y符号,y整数部分,x整数部分,x整数部分,y小数部分,y小数部分,],]
:param n: x的总位数
:param point: 小数位数
:return: 二进制基因型数据转换的数值
"""
# 在这个例子中,x,y的取值范围为-3~3,整数刚好整2位,加一位符号位,加上小数部分就-4~4了(为了不跑到图像外,修改一下图像范围),
# 小数部分不用太多,整个8位,就差不多够了,所以前11位x,后11位y,正负只看第一个符号,1正0负
# [x符号,x整数部分,x整数部分,x整数部分,x小数部分,x小数部分,······y符号,y整数部分,x整数部分,x整数部分,y小数部分,y小数部分,]
decode_data = []
for i in data: # 遍历每个个体,转码
x = Decoding_to_decimal(i[0:n], n, point)
y = Decoding_to_decimal(i[n:], n, point)
decode_data.append([x, y])
return decode_data
def Decoding_to_decimal(data, n, point):
# 仅一个x或y的转换
integer_len = n - point
decimal_data = 0
for i in range(1, integer_len): # 整数部分 2^n n=0,1,2···
decimal_data += data[i] * 2 ** (integer_len - i - 1)
for i in range(point): # 小数部分 1/2^n n = 1,2,3···
decimal_data += data[i + integer_len] / 2 ** (i + 1)
return (data[0] * 2 - 1) * decimal_data
def Get_gene_z(data): # 根据解码后数据,计算z值
"""
:param data: 全部基因型转码后的数据
:return: z值,z最大值,z最小值
"""
data_z = []
max_z = -float("inf")
min_z = float("inf")
for i in range(len(data)):
data_z.append(Function(data[i][0], data[i][1]))
if data_z[i] > max_z:
max_z = data_z[i]
if data_z[i] < min_z:
min_z = data_z[i]
return data_z, max_z, min_z
def Get_Fitness(data, max_data, min_data, maximum): # 计算适应度,这里用z的归一化加次方
"""
:param data: 需要计算的z值列表
:param max_data: z最大值
:param min_data: z最小值
:param maximum: 数值较大适应度高?
:return: 适应度列表
"""
# 之所以加个1e-3是为了让最小的也有活下去可能(来自i道i的仁慈)
gap = max_data - min_data # 最大最小值的差距
# 下面这里加点次方能更好的提升最大数值与最小数值的差距,保证较优秀的个体不会寄
if (maximum):
fitness = [((i - min_data) / gap)**1 + 1e-3 for i in data] # 归一化
else:
fitness = [((max_data - i) / gap)**1 + 1e-3 for i in data] # 归一化
return fitness
def Inheritance(parents, n): # 生育时,交叉+变异,可以扔进去多个个体
len_parents = len(parents) # 父辈个数
child = [] # 生出的孩子
for i in range(n + n): # 遍历每个基因点
child.append(parents[random.randint(0, len_parents - 1)][i]) # 随机继承某一个父辈的基因
# 假如我想每一轮,每个人都有10%概率突变,那么,当有11位数时,我需要 22个基因点突变概率x,
# (1-x)^22约等于0.9,解得x约为0.0048,整个0.005得了
if random.random() < 0.005:
child[i] = 0 if child == 1 else 1
return child
def Reproduction(number, data, n, strength): # 让新族群生育到原先族群大小
"""
:param number: 族群大小
:param data:生育前的族群基因
:param n: x的总位数
:param point: 小数位数
:return: 剩余完成的族群
"""
initial_len = len(data) # 初始个数
len_data = initial_len # 当前个数
if initial_len < 2:
print("种族没人")
while len_data < number: # 生够了就停下
parents = random.sample(data[0:initial_len], strength) # 对象包分配,不过是随机分配,不能和子代生育
data.append(Inheritance(parents, n)) # 生出的个体添加进族群
len_data += 1
return data
def Genetic_train(fig, gene_data, number, n, point, loop, x, y, z, maximum=True): # 遗传算法训练,带过程绘制
"""
:param fig: 窗口引用
:param gene_data: 基因型
:param number: 族群大小
:param n: x的总位数
:param point: 小数位数
:param maximum: 是否求函数最大值,默认是
:return: 最终的族群
"""
new_gene = gene_data # 开始的输入就是新族群
for i in range(loop): # 最大训练loop轮
# 物竞天择,适者生存
gene_data = new_gene
decode_data = Decoding(gene_data, n, point) # 解码
data_z, max_z, min_z = Get_gene_z(decode_data) # 计算z
fitness = Get_Fitness(data_z, max_z, min_z, maximum) # 求适应度
ax = Plot_Draw_F(fig, x, y, z) # 绘画出函数
Plot_Scatter(ax, decode_data, data_z, "blue") # 绘制全部个体
if max_z - min_z < 1e-2: # 认为训练完毕
break
# 开杀,每回死一半
len_gene = len(gene_data)
index_table = list(range(len_gene)) # 未选中的索引标志
new_gene = [] # 新族群
for j in range(len_gene // 2):
selected_elements = random.choices(index_table, weights=fitness) # 根据适应度,选中生存的个体
k = index_table.index(selected_elements[0]) # 根据选中的值,找到索引
new_gene.append(gene_data[k]) # 生存的个体进入新族群
decode_data.pop(k)
data_z.pop(k)
index_table.pop(k) # 活下来的不再选了
fitness.pop(k)
Plot_Scatter(ax, decode_data, data_z, "red") # 绘制死亡的个体
new_gene = Reproduction(number, new_gene, n, 2) # 让新族群生育到原先族群大小,两个人生
return new_gene
if __name__ == "__main__":
# 建立窗口
fig = plt.figure()
# 生成坐标网格
x, y, z = Get_Grid()
plt.pause(1) # 方便录像用,开窗口后等1秒再出图,你们建议删去
# 参数设置
number = 100 # 种群初始大小
point = 8 # 小数位数
n = point+3 # x或y长度
loop = 100 # 最大训练轮数
gene_data = Get_Random_gene(number, n) # 获得初始基因
gene_end = Genetic_train(fig, gene_data, number, n, point, loop, x, y, z) # 族群开始进化
# 显示图形,完成后不消失
plt.show()
注释写的比较清楚了,就不多解释了,
gene_end = Genetic_train(fig, gene_data, number, n, point, loop, x, y, z)
最后还可以再加一个参数maximum,True求最大值False求最小值,默认求最大值
贴一下所用函数的三视图,三个极大值,两个极小值



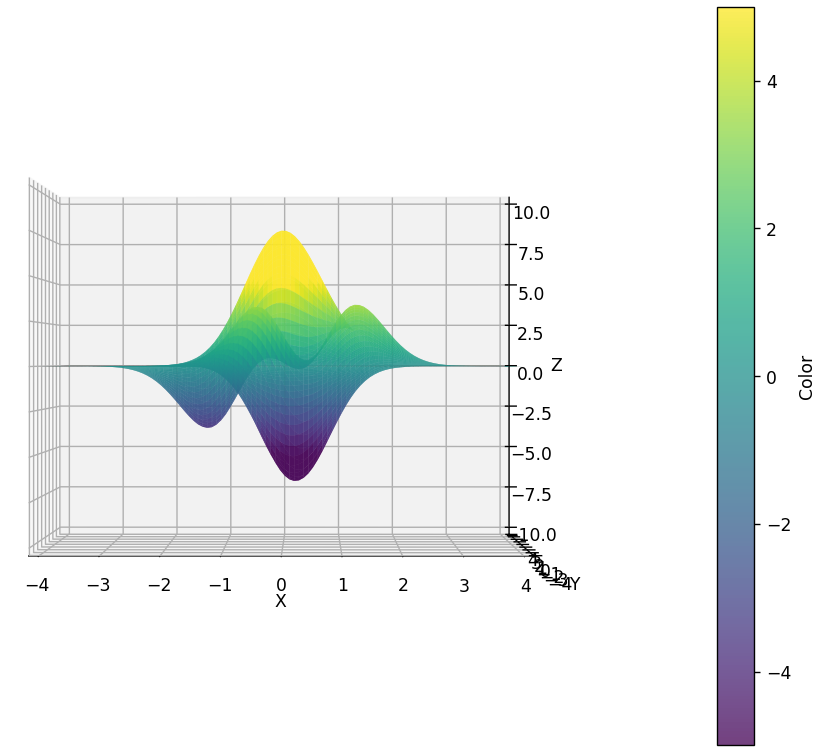
还想不明白,用这个主函数看一眼
if __name__ == "__main__":
# 建立窗口
fig = plt.figure()
# 生成坐标网格
x, y, z = Get_Grid()
Plot_Draw_F(fig,x,y,z)
# plt.pause(1) # 方便录像用,开窗口后等1秒再出图,你们建议删去
# # 参数设置
# number = 100 # 种群初始大小
# point = 8 # 小数位数
# n = point+3 # x或y长度
# loop = 100 # 最大训练轮数
# gene_data = Get_Random_gene(number, n) # 获得初始基因
# gene_end = Genetic_train(fig, gene_data, number, n, point, loop, x, y, z) # 族群开始进化
# 显示图形,完成后不消失
plt.show()初始代码结果:
视频挺长,蓝色的是初始族群,红色的是寄了的
遗传算法,初始代码结果
参数修改:
每一项修改都完成了上面的修改项,比如增加小数点位数的结果也修改了适应度计算。
修改适应度计算
通过训练过程,我们发现,有些跑到最大值附近的点,却没存活下来,这是因为我们使用的是
random.choices(index_table, weights=fitness)
通过weights的值,来决定存活下来的概率,值越大存活概率越高,因此,哪怕值比较高,依然有可能去世(先帝创业未半而中道崩殂),基于这点,我修改了适应度计算函数,让最高值和最低值之间的差距加大,使得优秀的个体更容易存活下来
def Get_Fitness(data, max_data, min_data, maximum): # 计算适应度,这里用z的归一化加次方
def Get_Fitness(data, max_data, min_data, maximum): # 计算适应度,这里用z的归一化加次方
"""
:param data: 需要计算的z值列表
:param max_data: z最大值
:param min_data: z最小值
:param maximum: 数值较大适应度高?
:return: 适应度列表
"""
# 之所以加个1e-3是为了让最小的也有活下去可能(来自i道i的仁慈)
gap = max_data - min_data # 最大最小值的差距
# 下面这里加点次方能更好的提升最大数值与最小数值的差距,保证较优秀的个体不会寄
if (maximum):
fitness = [((i - min_data) / gap)**5 + 1e-3 for i in data] # 归一化
else:
fitness = [((max_data - i) / gap)**5 + 1e-3 for i in data] # 归一化
return fitness通过实验,增加次方运算能帮助收敛,3次方有一定效果,5次方效果比较明显,更高次方效果显著。这里使用5次方为例,结果如下:
适应度计算公式修改后结果:
遗传算法,修改适应度代码结果
增加小数点位数
通过观察最后的结果,我们发现最后并没有到达最值点,这是因为我们使用二进制编码的方式来决定个体的x,y,使用了8位小数,这代表个体的取值其实是离散的,且最小粒度为2^-8 = 0.00390625
因此,我们可以通过增加小数位数,来使得最终收敛结果更加接近真正的最值点。
修改小数位数可以直接修改主函数中的point变量,这里我们以修改为21为例,2^-21=0.000000476837158203125
主函数修改:
if __name__ == "__main__":
# 建立窗口
fig = plt.figure()
# 生成坐标网格
x, y, z = Get_Grid()
plt.pause(1) # 方便录像用,开窗口后等1秒再出图,你们建议删去
# 参数设置
number = 100 # 种群初始大小
point = 21 # 小数位数
n = point+3 # x或y长度
loop = 100 # 最大训练轮数
gene_data = Get_Random_gene(number, n) # 获得初始基因
gene_end = Genetic_train(fig, gene_data, number, n, point, loop, x, y, z) # 族群开始进化
# 显示图形,完成后不消失
plt.show()增加小数点位数,确实能减少粒度,更趋近于最值点,但随着位数增多,收益会不断递减
增加小数点位数结果:
遗传算法,修改小数位数代码结果
修改存活个体数
我们可能下意识认为,减少存活个体数会加快收敛过程,但会更容易找到错误最值点,相对而言,增加存活个体数,虽然会使得收敛变慢,但找到的最值点更准确,也更能避免错误的收敛。
但实际使用时,我们会发现,增加存活个体数,因为每次死亡的个体少,所以出生的个体也少,导致变异的个体比较少,最后往往会因为没有变异个体早停,最后往往不能寻找到更好的最值点,总是差一些,减少存活个体数会导致留下的基因型少,但是生的多,更容易变异,反倒经常比增加存活个体数结果好。
修改Genetic_train函数,代码202行左右,这个for语句range(len_gene//2)更改为
保留1成个体
new_gene = [] # 新族群
for j in range(len_gene *1// 10):
selected_elements = random.choices(index_table, weights=fitness) # 根据适应度,选中生存的个体保留1成个体结果:
遗传算法,保留一成个体代码结果
保留9成个体
new_gene = [] # 新族群
for j in range(len_gene *9// 10):
selected_elements = random.choices(index_table, weights=fitness) # 根据适应度,选中生存的个体保留9成个体结果:
遗传算法,保留九成个体代码结果
酌情使用
增加初始个体数目:
无明显变化(计算时间除外)结果肯定是更好的,毕竟搜索的点更多了,但感觉不如多次取最好值。视频过长就不粘贴了