很久不接触数学了,machine learning需要用到一些数学知识,这里在重温一下相关的数学基础知识
矢量
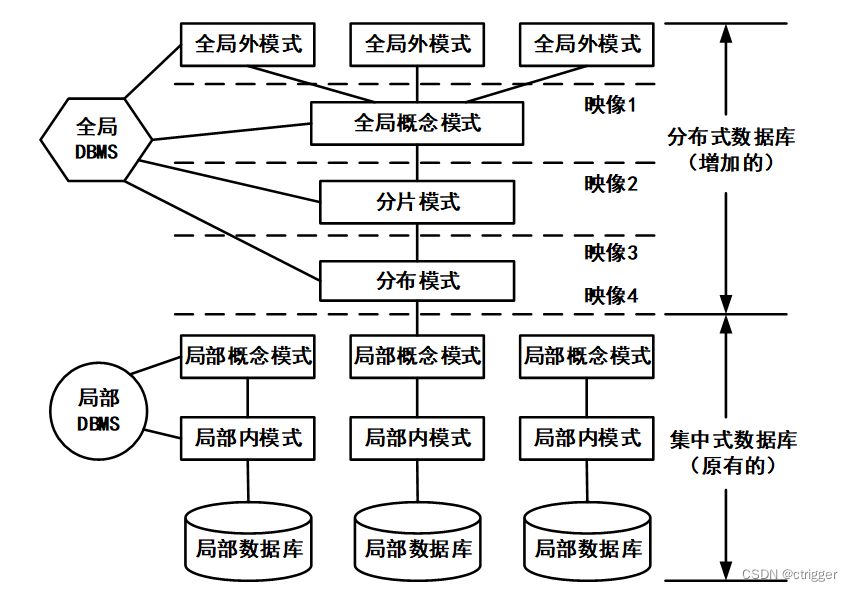
矢量是有序的数字数组。在表示法中,矢量用小写粗体字母表示。矢量的元素都是相同的类型。例如,矢量不包含字符和数字。数组中元素的数量通常被称为维度,数组中元素的数量通常被称为维度,可以使用索引引用矢量的元素。在数学设置中,索引通常从 1 到 n。在计算机科学和这些实验室中,索引通常从 0 运行到 n-1。下面是两个的对比,在计算机中我们使用的是左边code的那种方式,也就是0到n-1

Numpy中的阵列
NumPy 的基本数据结构是一个可索引的 n 维数组,其中包含相同类型 (dtype) 的元素。
一维向量的操作:
向量创建
创建一个指定shape的一维向量,参数可以是整数、元祖等等,参数表示要创建的序列的shape
a= np.zeros(4); print(f"np.zeros(4) : a = {a}, a shape = {a.shape}, a data type = {a.dtype}")
a= np.zeros((4,)); print(f"np.zeros(4,) : a = {a}, a shape = {a.shape}, a data type = {a.dtype}")
a= np.random.random_sample(4); print(f"np.random.random_sample(4): a = {a}, a shape = {a.shape}, a data type = {a.dtype}")创建一个不指定shape的一维向量
a = np.arange(4.); print(f"np.arange(4.): a = {a}, a shape = {a.shape}, a data type = {a.dtype}")
a = np.random.rand(4); print(f"np.random.rand(4): a = {a}, a shape = {a.shape}, a data type = {a.dtype}")创建指定值的一维向量
a = np.array([5, 4, 3, 2]); print(f"np.array([5,4,3,2]): a = {a}, a shape = {a.shape}, a data type = {a.dtype}")
a = np.array([5., 4, 3, 2]); print(f"np.array([5.,4,3,2]): a = {a}, a shape = {a.shape}, a data type = {a.dtype}")向量操作
获取向量元素:通过index和切片可以获得,这个和列表的操作相似。
-
通过index获得:
a = np.arange(10)
print(a)
# 获取Index = 2的元素
print(f"a[2].shape: {a[2].shape} a[2] = {a[2]}, Accessing an element returns a scalar")
# 获取最后一个元素
print(f"a[-1]={a[-1]}")
# index 必须在向量有效范围以内,否则会报错
try:
c = a[10]
except Exception as e:
print(e)- 切片获取元素
# 切片操作通过(start:stop:step)这个三个参数来控制要获取的元素,
# 切片操作是左闭右开,也就是包括index=start的值,但是不包括index=stop的值
# 向量切片操作
a = np.arange(10)
print(f"a = {a}")
#获取向量中的从index=2开始到Index=7结束的5个元素, 第三个参数1表示step=1,代表连续取值 (start:stop:step)
c = a[2:7:1]; print("a[2:7:1] = ", c)
# 获取向量中的从index=2开始到Index=7结束的元素, 第三个参数1表示step=2,代表隔一个index取一个值 (start:stop:step)
c = a[2:7:2]; print("a[2:7:2] = ", c)
# 取index 大于3的所有值
c = a[3:]; print("a[3:] = ", c)
# 取index小于3的所有值
c = a[:3]; print("a[:3] = ", c)
# 取所有的值
c = a[:]; print("a[:] = ", c)- 单个向量的操作
a = np.array([1, 2, 3, 4])
print(f"a: {a}")
# 将向量中的元素全部变为相反数
b = -a
print(f"b: {b}")
# 计算向量中所有元素的和并返回一个和的标量
b = np.sum(a)
print(f"b = np.sum(a) : {b}")
# 求向量的平均值
b = np.mean(a)
print(f"b = np.mean(a): {b}")
# 对向量中每个元素求平法
b = a**2
print(f"b = a**2 : {b}")- 对向量元素的操作,numpy很多对数字的操作也都是用于向量的
# 向量a+向量b, 两个向量长度必须相同,不然会报error
a = np.array([1, 2, 3, 4])
b= np.array([-1, -2, 3, 4])
print(f"Binary operators work element wise: {a + b}")
# 标量和向量的操作
a = np.array([1, 2, 3, 4])
b = 5 * a
print(f"b = 5 * a : {b}")- 向量与向量的点积

自定义一个实现点积的方法:
def my_dot(a,b):
"""
Compute the dot product of two vectors
Args:
a (ndarray (n,)): input vector
b (ndarray (n,)): input vector with same dimension as a
Returns:
x (scalar):
"""
x = 0
for i in range(a.shape[0]):
x= x+a[i]*b[i]
return x
# test my_dot()
a = np.array([1,2,3,4])
b = np.array([-1, 4, 3, 2])
print(f"my_dot(a, b) = {my_dot(a, b)}")使用Numpy中的点积方法:
# 使用numpy中的dot来计算点积,返回一个标量
a = np.array([1, 2, 3, 4])
b = np.array([-1, 4, 3, 2])
c = np.dot(a, b)
print(f"NumPy 1-D np.dot(a, b) = {c}, np.dot(a, b).shape = {c.shape} ")
c = np.dot(b, a)
print(f"NumPy 1-D np.dot(b, a) = {c}, np.dot(a, b).shape = {c.shape} ")然后对上面两种计算点积的方法做个效率上的对比
# 对比一下numpy 的dot和自己写的my_dot的效率如何,可以看出numpy中的效率要高很多
np.random.seed(1)
a = np.random.rand(10000000) # very large arrays
b = np.random.rand(10000000)
tic = time.time() # capture start time
c = np.dot(a, b)
toc = time.time() # capture end time
print(f"np.dot(a, b) = {c:.4f}")
print(f"Vectorized version duration: {1000*(toc-tic):.4f} ms ")
tic = time.time() # capture start time
c = my_dot(a,b)
toc = time.time() # capture end time
print(f"my_dot(a, b) = {c:.4f}")
print(f"loop version duration: {1000*(toc-tic):.4f} ms ")
del(a);del(b) #remove these big arrays from memory运行结果为:可以看到numpy的耗时要少很多
my_dot(a, b) = 24
NumPy 1-D np.dot(a, b) = 24, np.dot(a, b).shape = ()
NumPy 1-D np.dot(b, a) = 24, np.dot(a, b).shape = ()
np.dot(a, b) = 2501072.5817
Vectorized version duration: 6.5184 ms
my_dot(a, b) = 2501072.5817
loop version duration: 2430.3420 ms 矩阵
矩阵是一个二维阵列,里面的元素都是同一类型的。一般用大写黑体字母表示。用两个下标m,n表示,m表示行数,n表示列数。通过两个下标可以访问指定的元素
矩阵操作
创建矩阵
与创建向量的方法一样,只是这里的参数要换成元祖
a = np.zeros((1, 5))
print(f"a shape = {a.shape}, a = {a}")
a = np.zeros((2, 1))
print(f"a shape = {a.shape}, a = {a}")
a = np.random.random_sample((1, 1))
print(f"a shape = {a.shape}, a = {a}")
# 2.创建指定元素的矩阵
a= np.array([[5],
[4],
[3]])
print(f" a shape = {a.shape}, np.array: a = {a}")
矩阵的操作
# 3.矩阵的操作
# 3.1 下标访问
# reshape 是一种比较方便的方法创建矩阵,
a = np.arange(6).reshape(-1, 2) #reshape(-1,2) 表示生成一个6/2行,2列的矩阵,也就是3行两列的矩阵
print(f"a.shape:{a.shape},\na={a}")
# 访问一个元素
print(f"\na[2.0].shape:{a[2:0].shape},a[2,0]={a[2:0]}, type(a[2,0])={type(a[2,0])} Accessing an element returns a scalar\n")
# 访问一行
print(f"a[2].shape:{a[2].shape},a[2] = {a[2]},type(a[2]) = {type(a[2])}")
# 3.2切片访问
a = np.arange(20).reshape(-1, 10)
print(f"a=\n{a}")
# 访问一行中5个连续的元素(start:stop:step)
print("a[0,2:7:1]=",a[0, 2:7:1], "a[0,2:7:1].shape=", a[0, 2:7:1].shape, "a-1D array")
# 访问两行中5个连续的元素(start:stop:step)
print("a[:, 2:7:1] = \n", a[:, 2:7:1], ", a[:, 2:7:1].shape =", a[:, 2:7:1].shape, "a 2-D array")
# 访问矩阵所有元素
print("a[:,:] = \n", a[:,:], ", a[:,:].shape =", a[:,:].shape)
# 访问一行中的所有元素,方法1
print("a[1,:] = ", a[1,:], ", a[1,:].shape =", a[1,:].shape, "a 1-D array")
# 访问一行中的所有元素,方法2
print("a[1] = ", a[1], ", a[1].shape =", a[1].shape, "a 1-D array")