第一章 神经网络是如何实现的

神经网络不仅仅可以处理图像，同样也可以处理文本。由于处理图像讲起来比较形象，更容易理解，所以基本是以图像处理为例讲解的。

七、词向量

• 图像处理之所以讲起来比较形象，是因为图像的基本元素是像素，而像素是由数字表示的，可以直接处理。而文本的基本元素是词，要处理文本的话，首先要解决词的表示问题。

1. 独热（one-hot）编码

• 最简单的表示方法称作“独热”（one-hot）编码。

2. 独热编码举例

• 我们举例说明独热编码方法。假设有一句话：我在清华大学读书，生活在美丽的清华园中。我们以这句话中出现的词组成一个共有8个词的词表：
• {我，在，清华大学，读书，生活，美丽的，清华园，中}
• 独热编码方法就是用一个与词表等长的向量表示一个词，该向量只有一个位置为1，其他位置均为0。具体哪个位置为1呢？就看单词在词表中处于第几位，如果处于第n位，那么在向量的第n个位置就为1。这也是“独热编码”一词的来源。
• 比如“清华大学”一词处于词表的第3个位置，则该词就可以表示为：
  • “清华大学”=[0，0，1，0，0，0，0，0]
• 同样的，“清华园”、“美丽的”分别可以表示为：
  • “清华园”=[0，0，0，0，0，0，1，0]
  • “美丽的”=[0，0，0，0，0，1，0，0]
    

3. 独热编码的特点

• 这种表示的优点是比较简单，事先做好一个词表，词表确定后词的表示就确定了。但有很多不足。比如：如果处理真实文本，常用词至少需要10万个，每个词都需要表示为一个长度为10万的向量。也无法通过计算的办法获得两个词的相似性。比如在自然语言处理中，常常用欧氏距离衡量两个词的相似性或者是否近义词，欧氏距离越小，就说明两个词越相似。但是对于独热编码来说，任何词都只有一个位置为1，且只要是非同一个词，则1的位置一定是不一样的，所以任何两个词的欧氏距离都是 $\sqrt{2}$ ，比如“清华大学”与“清华园”的欧氏距离为：
  $${\Vert \begin{array}{c}“清华大学”-“清华园”\end{array}\Vert }_2$$
  $$=\sqrt{(0-0{)}^2+(0-0{)}^2+(1-0{)}^2+(0-0{)}^2+(0-0{)}^2+(0-0{)}^2+(0-1{)}^2+(0-0{)}^2}$$
  $$=\sqrt{2}$$
• “美丽的”与“清华园”的欧氏距离为：
  $${\Vert \begin{array}{c}“美丽的”-“清华园”\end{array}\Vert }_2$$
  $$=\sqrt{(0-0{)}^2+(0-0{)}^2+(0-0{)}^2+(0-0{)}^2+(0-0{)}^2+(1-0{)}^2+(0-1{)}^2+(0-0{)}^2}$$
  $$=\sqrt{2}$$
  
• 从语义的角度来说，理应“清华大学”与“清华园”的距离应该小于“美丽的”与“清华园”的距离才比较合理。

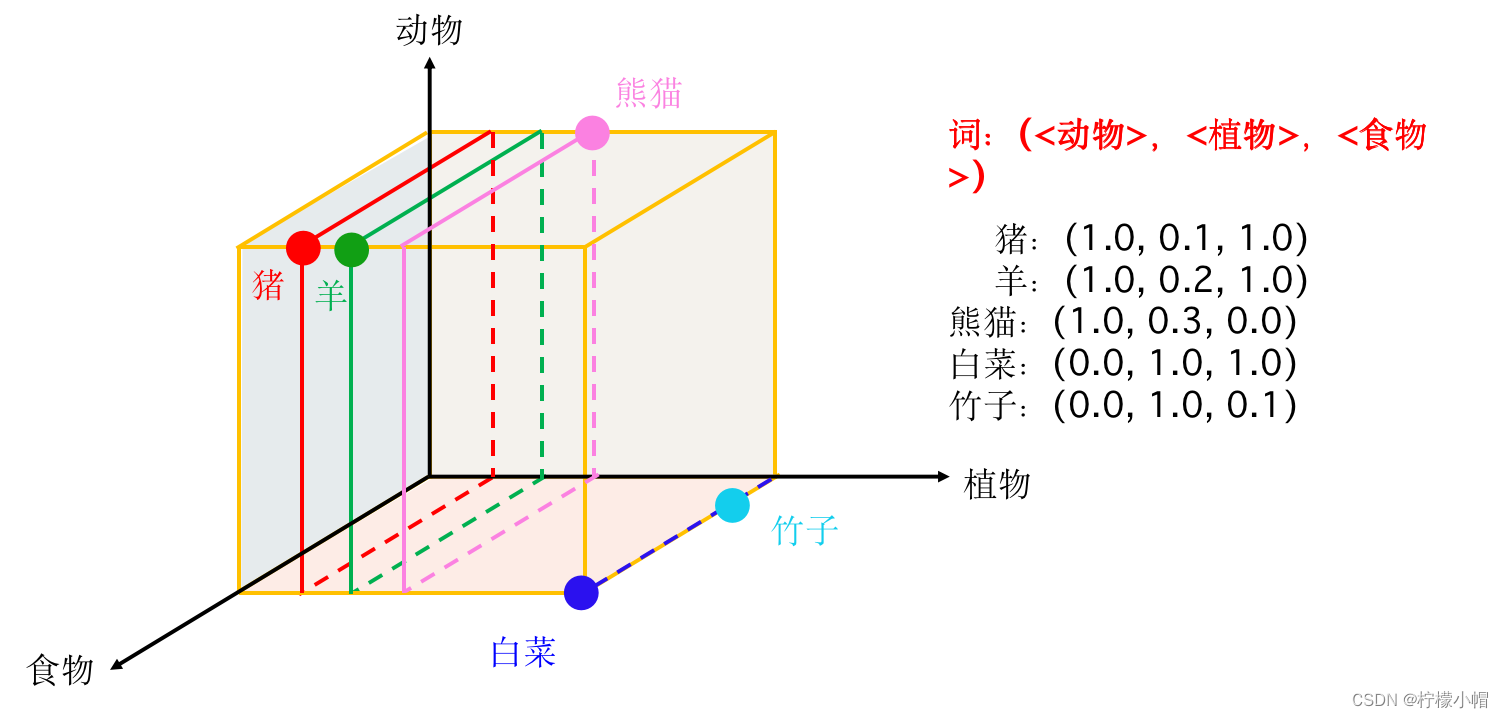
4. 词的分布式表示

• 为了解决独热编码存在的不足，研究者提出了“稠密”向量表示方法，还是用向量表示一个词，但是不再是一个向量只有一位为1，其余为0了，而是向量的每一位都有具体的数值，这些数值“联合起来”表示一个词。由于“动用”了向量的每一位表示一个词，所以向量长度也没有必要和词表一样长，一般长度只需要几百位就可以了。而且还可以利用向量间的距离求解两个词的语义相似性。

• 这种稠密表示方法一般是通过训练得到的。
  
  
• 得先从神经网络语言模型开始讲起。

5. 语言模型

6. 神经网络语言模型

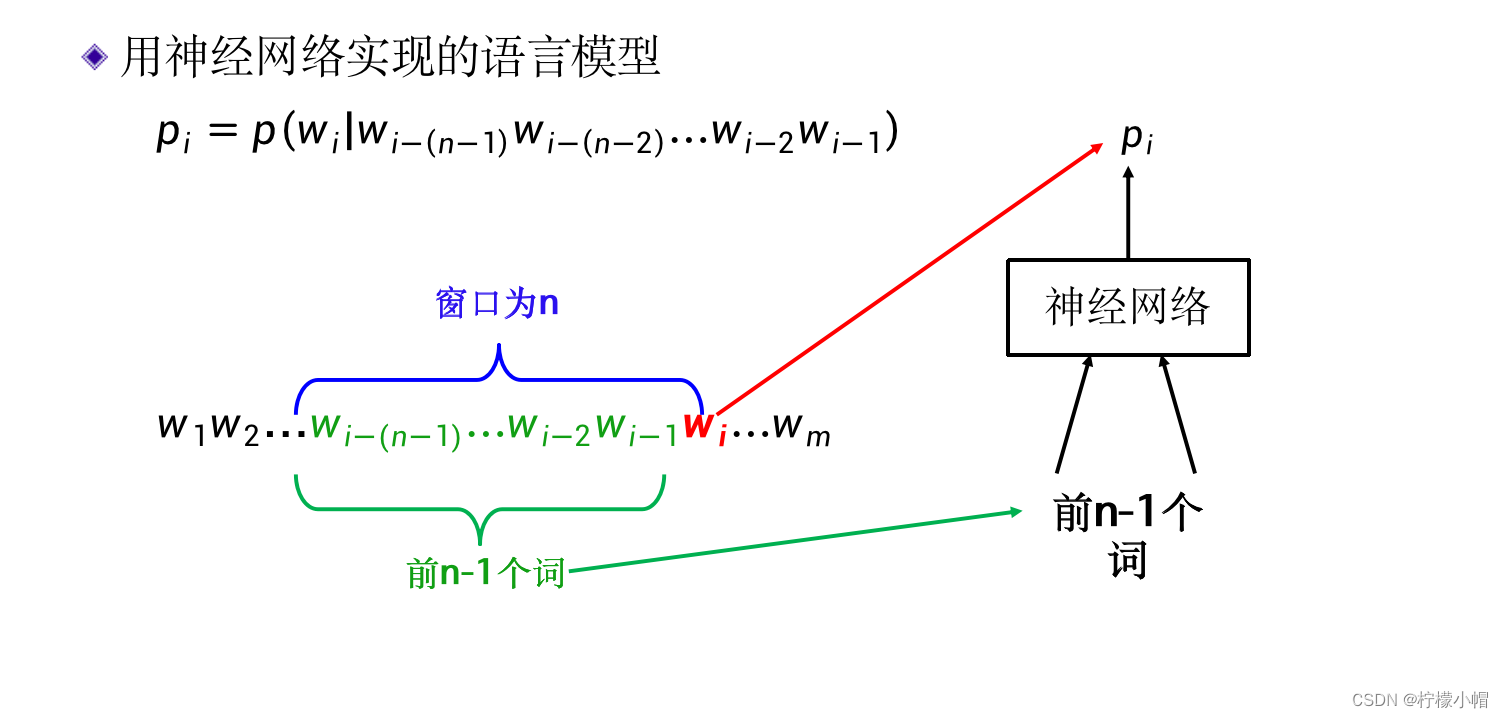
• 简单地说，当给定了一句话的前n-1个词后，预测第n个词是什么词的概率，这样的一个预测模型称为语言模型。比如给定了前4个词是“清华大学”、“计算机”、“科学”、“与”，那么第5个词可能是什么词呢？第5个词是“技术”的可能性比较大，因为这句话很可能是说“清华大学计算机科学与技术”。第5个词是“工程”的可能性也不小，因为“清华大学计算机科学与工程”也比较通顺。但是如果是“清华大学计算机科学与白菜”，虽然从语法层面这句话也没有啥问题，但是很少出现将“计算机科学”和“白菜”并列的情况，所以第5个词是“白菜”的概率就非常小了。语言模型就是用来评价一句话是否像“人话”，如果像“人话”则概率大，否则就概率小，甚至为0。如果语言模型是用神经网络实现的，则称为神经网络语言模型。

• 这里说的前n-1个词不一定是从一句话的开始计算，从一句话的任意一个位置开始都是可以的，总之当前词前面的n-1个词就可以，而不管当前词具体在哪个位置。如果前面不足n-1个词，则有几个算几个。比如当前词在第t个位置，则其前面n-1个词为 $w_{t-n+1}{w}_{t-n+2}\cdots w_{t-2}{w}_{t-1}$ ，这n-1个词称作 $w_t$ 的“上下文”，用 $context(w_t)$ 表示，其中 $w_i$ 表示词，n被称作窗口的大小，表示只考虑窗口内的n个词。
  

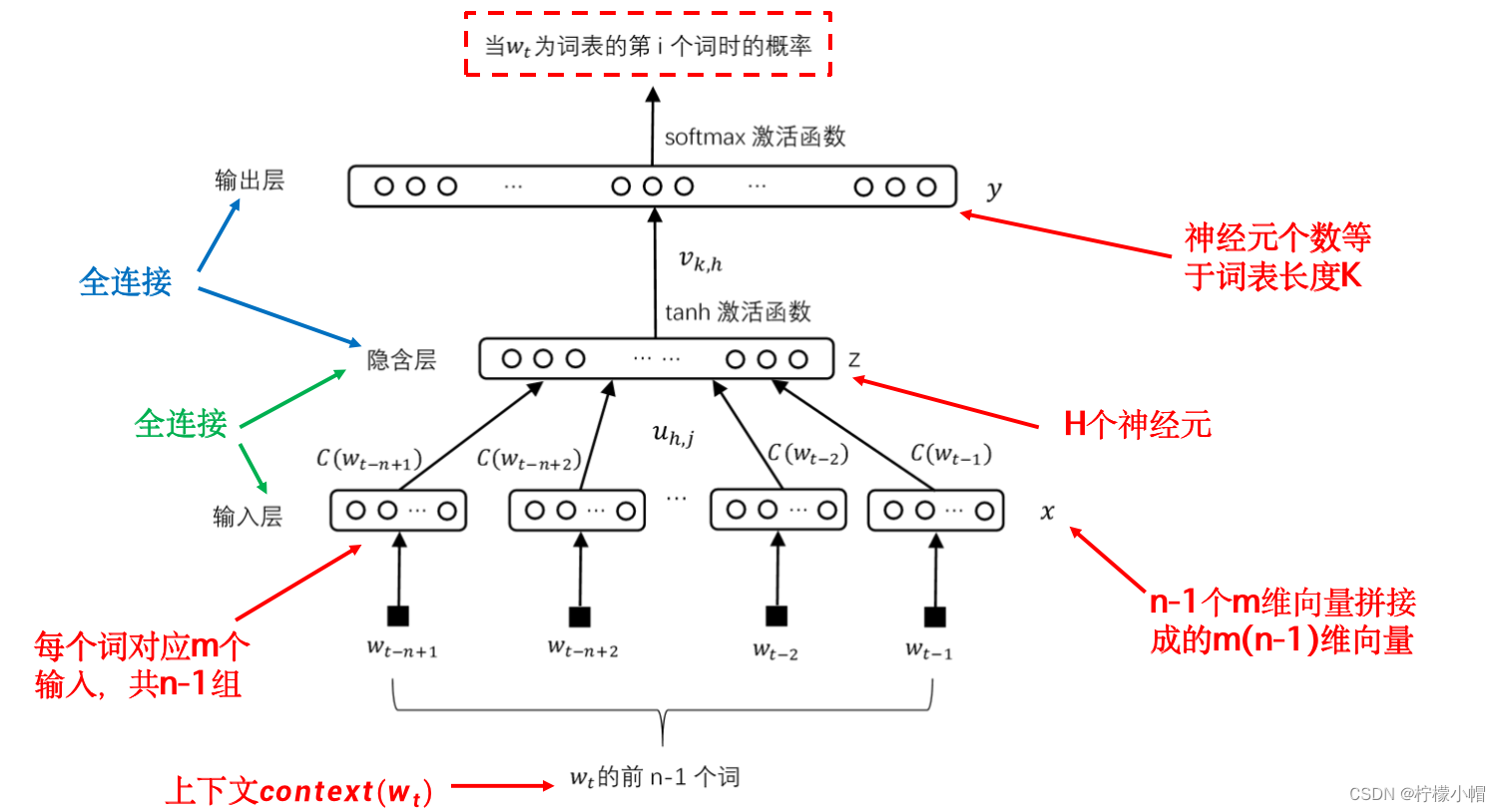
• 下图给出了一个最常见的用全连接神经网络实现的神经网络语言模型示意图。
  

• 图示的语言模型就是一个全连接神经网络，与普通的全连接网络不同的是，输入层分成了(n-1)组，每组m个输入，共(n-1)m个输入。每组输入共m个数值组成一个向量，对应 $w_t$ 的上下文的一个词，该向量用 $C(w_{t-l})(l=1,2,...,n-1)$ 表示。所有的 $C(w_{t-l})$ 拼接在一起组成一个长度为(n-1)m的向量，用 $x=[x_1,x_2,...,x_{(n-1)m}]$ 表示。如果不考虑分组的话，与普通全连接神经网络的输入层是一样的，也就是x是输入。

• 为什么要对输入分组呢？

  • 每一组输入组成的向量对应当前上下文的一个词，当上下文发生变化时，要通过查表的办法将组成上下文的词对应的向量取出来，放到神经网络输入层的相应位置。为此在构建神经网络语言模型时，首先要确定一个词表，这个词表通常很大，要包含所有可能出现的词，通常有几十万个词。每个词对应一个长度为m的向量，并在词和向量之间建立某种联系，以便需要时可以方便地取出来。

• 长度为m的向量如何得到暂时不着急，现在只需知道一个词对应一个向量就可以了，后面再说如何得到这个向量。

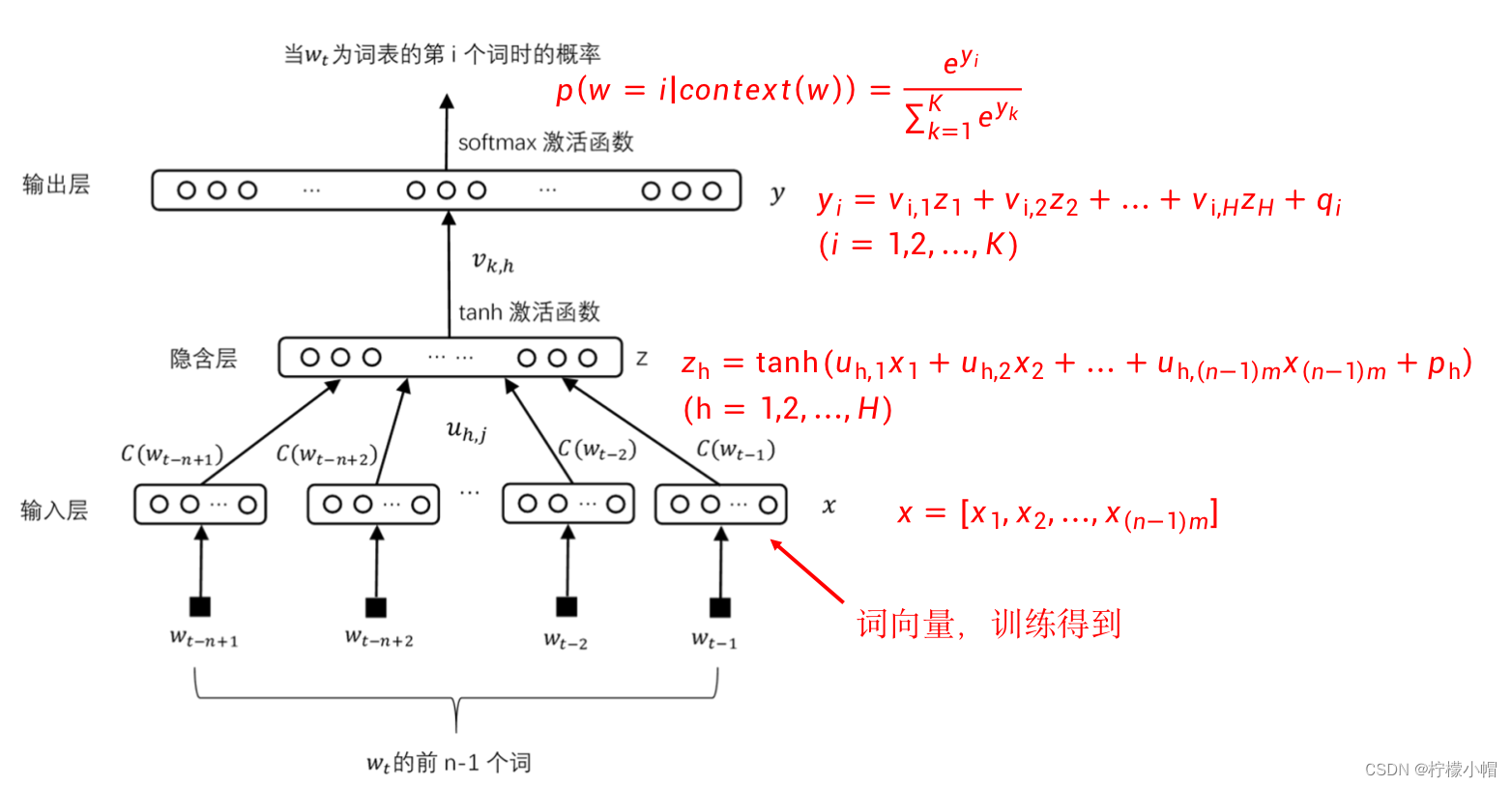
• 接下来看图的隐含层，这一层没啥特殊性，就是普通的隐含层，共H个神经元，每个神经元都与输入层的神经元有连接，权重为 $u_{h,j}$ ，表示输入层第j个输入到隐含层第h个神经元的连接权重。隐含层的每个神经元连接一个双曲正切激活函数（tanh）作为该神经元的输出。隐含层所有神经元的输出组成向量 $z=z_1,z_2,...,z_H$ ，第h个神经元的输出用公式表示如下：
  $$z_h=tanh(u_{h,1}{x}_1+u_{h,2}{x}_2+\cdots +u_{h,(n-1)m}{x}_{(n-1)m}+p_h)$$

• 其中 $p_h$ 为第h个神经元的偏置。

• 输出层神经元的个数与词表的大小一致，一个神经元对应一个词，神经元连接softmax激活函数得到输出结果，每个神经元的输出值表示在当前上下文下， 为该神经元对应的词时的概率。例如：假定输出层的第3个神经元对应“技术”一词，第5个神经元对应“工程”一词，当上下文为“清华大学 计算机 科学 与”时，则输出层第3个神经元的输出值就表示“清华大学 计算机 科学 与”之后连接“技术”一词的概率，而第5个神经元的输出值表示“清华大学 计算机 科学 与”之后连接“工程”一词的概率。

• 从隐含层到输出层也是全连接，每个输出层的神经元都与隐含层的神经元有连接，权重为 $v_{k,h}$ ，表示隐含层第h个神经元到输出层第k个神经元的连接权重。为了在输出层得到一个概率输出，最后加一个softmax激活函数。假设输出层所有神经元在连接激活函数前的输出组成向量 $y=y_1,y_2,\cdots ,y_K$ ，其中K为词表长度，则第k个神经元的输出用公式表示如下：
  $$y_k=v_{k,1}{z}_1+v_{k,2}{z}_2+\cdots +v_{k,H}{z}_H+q_k$$

• 其中 $q_k$ 为输出层第k个神经元的偏置。

• 加上softmax激活函数后，输出层第k个神经元的输出为：
  $$p(w=k|context(w))=\frac{e^{y_k}}{{\sum }_{i=1}^K{e}^{y_i}}$$

• 表示的是输出层第k个神经元所对应的单词w出现在当前上下文后面的概率。

• 如何确定输出层哪个神经元对应哪个词呢？

  • 这个是人为事先规定好的，哪个神经元对应哪个词并不重要，只要事先规定好一个神经元对应唯一的词就可以了。

• 那么这个神经网络语言模型如何训练呢？

7. 如何训练神经网络语言模型？

7.1 训练样本

• 为了训练这个模型，需要有训练样本，对于语言模型来说，样本就是一个含有n个词的词串，前n-1个词就是上下文，第n个词相当于标记。我们可以收集大量的文本构成训练语料库，库中任意一个长度为n的连续词串就构成了训练样本。比如语料库中有语句“清华 大学 计算机 科学 与 技术 系”，假定窗口大小为5，则“清华 大学 计算机 科学 与”、“大学 计算机 科学 与 技术”、“计算机 科学 与 技术 系”都是训练样本。

7.2 损失函数

• 有了训练样本后，还需要定义一个损失函数。我们先看一个例子。假定语料库就三句话：“计算机 科学”、“计算机 科学”，“计算机 工程”，窗口大小为2，我们希望通过该语料库估计出两个概率值：p(科学|计算机)和p(工程|计算机)，分别表示当前一个词为“计算机”时，后一个词为“科学”的概率和后一个词为“工程”的概率。这两个概率分别取多少才是合理的呢？语料库中的三句话可以看成是3个样本，我们假定这3个样本的出现是独立的，所以他们的联合概率可以用各自出现概率的乘积表示，即：
  $$p(“计算机科学”，“计算机科学”，“计算机工程”)$$
  $$=p(科学|计算机）\cdot p(科学|计算机)\cdot p(工程|计算机)$$
  $$=p(科学|计算机{)}^2\cdot p(工程|计算机)$$

• 由于这个例子中“计算机”后面出现的词只有“科学”和“工程”两种可能，所以在“计算机”后面出现“科学”或者“工程”的概率和应该等于1，即：
  $$p(科学|计算机)+p(工程|计算机)=1$$
• 所以有：
  $$p(“计算机科学”，“计算机科学”，“计算机工程”）$$
  $$=p(科学|计算机{)}^2(1-p(科学|计算机))$$
  
• 对于不同的概率取值，p(“计算机 科学”，“计算机 科学”，“计算机 工程”)的值是不同的，比如当p(科学│计算机)=0.5时：
  $$p(“计算机科学”，“计算机科学”，“计算机工程”）$$
  $$=0.5^2\cdot (1-0.5)=0.125$$
• 而当p(科学│计算机)=0.6时：
  $$p(“计算机科学”，“计算机科学”，“计算机工程”）$$
  $$=0.6^2\cdot (1-0.6)=0.144$$

7.3 合理概率

• 概率取多大才应该是合理的呢？
  • 目前我们只有语料库提供的三句话，所以只能以这三句话为依据进行估计，既然这三个样本同时出现了，那么我们就应该接受这个事实，让他们的联合概率最大，所以估计概率的原则就是当p(科学│计算机)取值多少时，能使他们的联合概率最大。
  • 求最大值只需要令联合概率的导数等于0，就可以求解了。

$$p(“计算机科学”，“计算机科学”，“计算机工程”）的导数$$
$$=p(科学|计算机{)}^2(1-p(科学|计算机))的导数$$
$$=2p(科学|计算机)3p((科学|计算机){)}^2$$
$$令2p(科学|计算机)3p((科学|计算机){)}^2=0，有$$
$$2-3p(科学|计算机)=0$$

• 所以：
  $$p(科学|计算机)=\frac{2}{3}$$
• 由于：
  $$p(科学|计算机)+p(工程|计算机)=1$$
• 所以：
  $$p(工程|计算机)=\frac{1}{3}$$
• 这个结果是不是与我们直观想象的结果也是一致
  

7.4 最大似然估计

• 通过让联合概率最大化估计概率的方法称作最大似然估计。但是一般来说并不是直接估计概率值，因为一般来说联合概率分布是一个含有参数的函数，而是通过最大似然方法估计该联合概率分布的参数。对于神经网络语言模型来说，概率是用神经网络表示的，所以就是估计神经网络的参数。根据我们前面介绍过的神经网络语言模型（见下图），对于语料库中的任何一个词w，我们假定窗口大小为n，依据w在语料库中的位置，会有一个w的上下文context(w)，也就是w的前n-1个词，以context(w)作为神经网络语言模型的输入，在输出层词w所对应的位置k会得到一个输出值，该值表示的是在给定的上下文下，下一个词是w的概率。依据最大似然估计方法，我们希望在该语料库上，所有词在给定上下文环境下的概率乘积最大。即：
  $$\underset{\theta }{\max }\underset{wϵC}{\Pi }p(w=k|context(w),\theta )$$

• 其中 $\theta$ 表示神经网络的所有参数，C表示语料库，符号“ $\Pi$ ”表示连乘的意思。式子 $\underset{wϵC}{\Pi }p(w=k|context(w),\theta )$ 称为似然函数。所以，我们的目标就是训练神经网络语言模型，确定参数 $\theta$ ，使得似然函数在给定的训练集上最大。

• 训练神经网络一般是用BP算法求损失函数最小，这里是要求最大，所以需要通过一个变换就可以将最大化问题转化为最小化问题。为了计算方便，我们首先通过对似然函数做对数运算，将连乘变换为连加，因为经过对数运算后，原来的连乘就变换为连加了。

$$\underset{\theta }{\max }\underset{wϵC}{\Pi }p(w=k|context(w),\theta )$$

• 取对数后为：
  $$\underset{\theta }{\max }log\underset{wϵC}{\Pi }p(w=k|context(w),\theta )$$
  $$=\underset{\theta }{\max }\sum _{wϵC}logp(w=k|context(w),\theta )$$
• 如果我们在上式前面增加一个“负号”，原来的最大化就可以变成最小化问题了：
  $$\underset{\theta }{\min }(-\sum _{wϵC}logp(w=k|context(w),\theta ))$$

• 这样我们就可以用下式作为损失函数，然后用BP算法求解。
  $$L(\theta )=-\sum _{wϵC}logp(w=k|context(w),\theta )$$
• 其中 $-\sum _{wϵC}logp(w=k|context(w),\theta )$ 称为负对数似然函数。
• 这样一来，这个神经网络语言模型就跟普通的全连接神经网络没有任何区别了。