【数据结构】八大排序算法-代码实现+复杂度分析+稳定性分析+总结

news2025/2/23 2:30:57

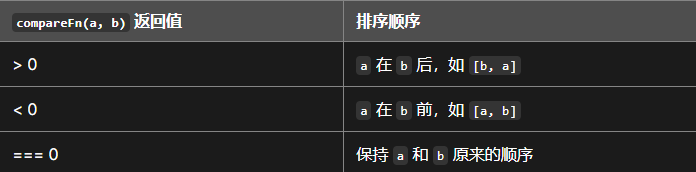
文章目录

  • 关于稳定性
  • 插入排序
    • 直接插入排序
    • 希尔排序
  • 选择排序
    • 直接选择排序
    • 堆排序
  • 交换排序
    • 冒泡排序
    • 快速排序
      • hoare版本
      • 挖坑法
      • 两路划分
    • 快排致命点
      • 三路划分
      • 小区间优化
    • 快排非递归
  • 归并排序
    • 非递归版本
  • 计数排序-鸽巢原理
    • 绝对映射
    • 相对映射
  • 插入排序和选择排序的对比
  • 总结

关于稳定性

数组中相同的值，在排序之后相对位置是否发生变化，如果会改变，就不稳定，能保证不变就是稳定

OJ测试链接：https://leetcode.cn/problems/sort-an-array/

插入排序

直接插入排序

核心思想：把后一个数插入到前面的有序区间，使得整体有序

比如说：[0，end]是有序的区间，x是end的下一个位置的元素，此时要做的就是将x插入到这个有序区间，使得[0，x]变有序

  • 从[0，end]区间找到一个符合x插入的位置，然后插入到对应位置
void InsertSort(vector<int>& v)
{
    int n =  v.size();
    for(int i = 0;i<n-1;i++) //注意:i的范围是[0,n-2]
    {
        //思想:将x插入到[0,end]的有效区间
        int end = i;
        int x = v[end+1];
        while(end >= 0) //找到合适的位置插入
        {
            if(v[end] > x)
            {
                v[end+1] = v[end]; //当前元素往后挪
                end--;//下一轮判断,前一个数和x比较
            }
            else 
                break;//找到插入位置了
        }
        v[end + 1] = x;//插入到此时的end位置的后面
    }
}

时间复杂度分析

最坏情况(数组元素逆序)：每次插入，元素都要往后移动

  • 移动次数：1 +2 +3…+ n => 等差数列 ==>O(N^2)

最好情况：(接近有序或者有序)，基本不用移动数据 ->O(N)

空间复杂度：O(1)

稳定性：它是一种稳定的排序算法，因为相同元素比较时，我们是插入到它的后面

稳定性：稳定

  • 将x插入到[0,end]的有序区间的时候，当区间元素和x的值相同的时候，是将x插入到该区间元素后面，二者的相对顺序不变

希尔排序

基本思想是：

  • 1.先选定一个gap，把待排序数据分组，所有距离为gap分在同一组内，并对每一组内的记录进行排序。

    • 预排序：目的是让数组更接近于有序，这样子后续gap为1进行直接插入排序，效率就是O(N)

  • 2.然后取重复上述分组和排序的工作，当到达gap=1时，就是直接插入排序，整体就有序了

  • gap越大：预排序越快，预排序后越不接近有序

  • gap越小：预排序越慢，预排序后越接近有序

什么时候预排序的效果最好：数据是逆序的时候，预排序完成就接近有序

时间复杂度：O(N^1.3)

稳定性：不稳定

  • 相同的值,预排序时可能分到不同的组里面,导致相对顺序发生改变

写法1：多组一起预排序

void ShellSort(vector<int>& v)
{
    int n =  v.size();
    int gap = n; //gap为几就分为几组, 预排序
    while(gap > 1)
    {
        //目的是为了保证最后能让gap为1,进行直接插入排序
        gap = gap / 3 + 1; //或者:gap = gap / 2 
        //写法1:一锅炖
        for(int i = 0 ;i < n - gap;i++) //注意:i的范围！ 否则end+gap会越界
        {
            int end  = i;//end的范围:[0,n- gap -1]
            int x = v[end + gap];//i的范围:[gap,n - 1]
            while(end >= 0)
            {
                if(v[end] > x)
                {
                    v[end + gap] = v[end];//把a[end]往后移动,以gap为间隔的为一组,所以移动到a[end+gap]位置
                    end -= gap;//下一轮循环,以gap为间隔的为一组,前一个数(end-gap位置对应的值)和x比较
                }
                else 
                    break;
            }
            v[end + gap] = x;//以gap为间隔的为一组,把x放在end + gap位置
        }
    }
}

写法2：每一组分别进行预排序

  • 一次只排序间隔为gap的元素(同组元素)，一共有gap组，所以要循环gap次

需要变动的位置：循环gap次，每次处理一组！

  • 每一组的起始位置是当前组的组号，然后每次变化范围:+=gap
void ShellSort(vector<int>& v)
{
    int n =  v.size();
    int gap = n; //gap为几就分为几组, 预排序
    while(gap > 1)
    {
        //目的是为了保证最后能让gap为1,进行直接插入排序
        gap = gap / 3 + 1; //或者:gap = gap / 2 

        //gap组,每组单独排序
        for(int j = 0;j<gap;j++)
        {
            for(int i = j ;i < n - gap;i+=gap) //注意:i的初始值！！和变动范围 i+=gap
            {
                int end  = i;//end的范围:[0,n- gap -1]
                int x = v[end + gap];//i的范围:[gap,n - 1]
                while(end >= 0)
                {
                    if(v[end] > x)
                    {
                        v[end + gap] = v[end];//把a[end]往后移动,以gap为间隔的为一组,所以移动到a[end+gap]位置
                        end -= gap;//下一轮循环,以gap为间隔的为一组,前一个数(end-gap位置对应的值)和x比较
                    }
                    else 
                        break;
                }
                v[end + gap] = x;//以gap为间隔的为一组,把x放在end + gap位置
            }
        }


    }
}

选择排序

直接选择排序

**思想：**每次从要排序的区间当中找到最大和最小的数，如果是排序，那么把他区间的最大的数和区间右端点对应值交换，把区间中最小的数和区间左端点对应值交换，然后缩小区间重复上述步骤，直到区间只有一个数

时间复杂度：遍历一遍才能选出一个数或者两个数，无论什么情况都是O(N^2)

稳定性：不稳定

  • 在区间当中找到最大和最小的数和区间左右端点位置的值交换，可能会导致两个相同的值相对顺序发生变化

image-20220926145213786

方法1：每次选择一个数

void SelectSort(vector<int>& v)
{
    int n = v.size();
    int end = n-1;
    while(end > 0)//当区间只有一个元素就不需要选了所以循环条件为：end > 0
    {
        int maxIndex = 0;
        //从[0,end]区间选取一个数放到end位置
        for(int i = 0;i<=end;i++)
        {
            if(v[i] > v[maxIndex])  //更新最大值所在位置的下标
                maxIndex = i;
        }
        ::swap(v[end],v[maxIndex]);
        end--;//缩小区间
    }
}

方法2：每次选择两个数

void SelectSort(vector<int>& v)
{
    int n = v.size();
    int begin = 0,end = n -1;
    while(begin < end)
    {
        //在[begin,end]区间找出最大最小的位置
        int maxIndex = begin,minIndex = begin;
        for(int i = begin;i<=end;i++)
        {
            if(v[i] > v[maxIndex]) maxIndex = i;
            if(v[i] < v[minIndex]) minIndex = i;
        }
        ::swap(v[begin],v[minIndex]);//最小值放到begin位置

        //坑点：如果begin和maxIndex一样
        //因为下面一步begin位置和值已经和minIndex位置交换了,所以就导致了minIndex位置放的才是最大值了
        //所以需要特判一下,如果begin和maxIndex相同,那么经过上面一步交换之后,minIndex位置放的才是最大值
        if(begin == maxIndex) 
            maxIndex = minIndex;
        ::swap(v[end],v[maxIndex]);//最大值放到end位置

        begin++,end--;//缩小区间
    }
}

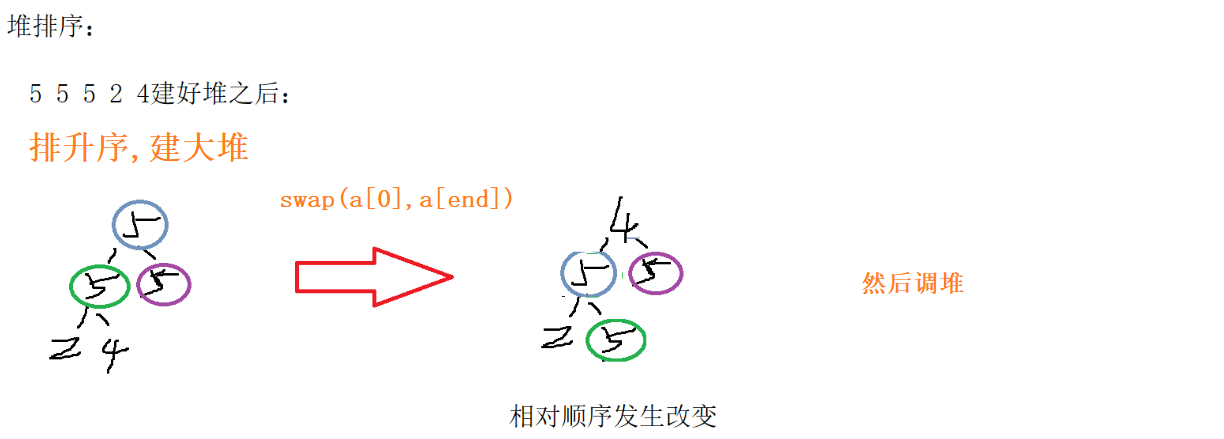
堆排序

排升序 建大堆     排降序   建小堆

建堆的方法：

向上调整：数组的第一个元素认为是堆，然后从第二个元素开始，把数组的每个元素插入堆中，然后向上调整

  • 向上调整建堆 O(N*logN)

向下调整：从最后一个叶子结点的父亲开始调整

  • **向下调整建堆：O(N) **

1.首先需要先建堆，只需要从最后一个叶子结点的父节点开始，在数组当中从后往前去向下调整即可

  • 共n个元素，最后一个结点的下标为: n -1
  • 它的父亲结点的下标为:parent = (child - 1)/2 = (n - 1- 1)/2

2.建好堆之后，将堆顶数据与堆的最后一个数据交换，然后对根位置进行一次堆的向下调整，但是调整时被交换到最后的那个数不参与向下调整，然后缩小堆中有效数据个数，剩下的元素进行向下调整，其余数又成一个大堆…重复上述步骤，直到堆中只剩下一个元素

时间复杂度分析：无论哪种方法建堆：都是O(N*logN)

  • 建堆的时间复杂度 + 调堆的时间复杂度 N*logN

稳定性：不稳定

  • 在调堆的时候，可能会导致相同元素的相对顺序改变

image-20220926145413716

//排升序 建大堆
void AdjustDown(vector<int>& v,int parent,int n) //从哪个位置向下调整,堆中有效元素个数
{
    int child = parent * 2 + 1; //左孩子
    while(child < n) //最坏情况：调整到叶子节点
    {
        if(child + 1 < n && v[child + 1] > v[child]) //选出较大的孩子
            child += 1;
        if(v[child] > v[parent])
        {
            ::swap(v[child],v[parent]); 
            //向下迭代
            parent = child;
            child = parent*2+1;
        }
        else 
            break; //已经是大堆了
    }
}

void HeapSort(vector<int>& v)
{
    int n = v.size();
    //1.从最后一个节点(下标:n-1)的父节点((child - 1 )/ 2)开始建堆(向下调整建堆)
    for(int i = (n - 1 - 1 )/ 2;i>=0;i--)
        AdjustDown(v,i,n);
    //2.调堆
    int end = n-1;//认为是堆中有效元素的个数 & 当前堆顶元素应该交换之后放的位置
    while(end > 0)
    {
        ::swap(v[end],v[0]);
        AdjustDown(v,0,end);//从根节点开始向下调整,认为堆中元素个数为end个
        end--;
    }
}

如果使用的是向上调整建堆：

//排升序 建大堆
void AdjustUp(vector<int>& v,int child)
{
    int parent = (child - 1) / 2;
    while(parent >= 0) //最坏情况：调整到根节点(根节点可能也要和其孩子交换,所以条件是>=)
    {
        if(v[child] > v[parent])
        {
            ::swap(v[child],v[parent]);
            //向上迭代
            child = parent;
            parent = (child - 1
                     ) / 2;
        }
        else 
            break;//堆已经构建好了
    }
}

//建堆
//1.第一个元素认为是堆，然后从第二个元素开始每个元素都进行向上调整
for(int i = 1; i<n;i++)
    AdjustUp(v,i);

交换排序

冒泡排序

主要思想：相邻元素之间进行比较交换

假设排升序，一趟冒泡可以排序一个数，使最大的元素沉到最后面，那么下一轮排序就可以不比较已经排好序的元素

  • n个元素，只需排序n-1次，就可以让n个数有序

优化：如果提前有序了（某一趟冒泡当中没有元素交换），就不需要再冒泡了

时间复杂度：

  • 最坏情况：第一轮：N个数比较交换，第二轮：N-1个数比较交换… ，此时相当于是等差数列，复杂度为O(N^2)
  • 最好情况：数组接近有序/有序，某一趟冒泡当中没有元素交换直接结束，O(N)

稳定性：稳定

  • 相邻元素进行比较,相同的元素之间不进行交换
void BubbleSort(vector<int>& v)
{
    int n = v.size();
    //每一趟可以确定一个元素到准确位置,n个元素只需要进行n-1趟
    for(int i = 0;i<n-1;i++)
    {
        bool flag = true;//是否已经有序
        //每一趟都可以少比较一个已经确定好的数
        for(int j = 0;j<n - 1 - i;j++) //注意:j<n-1-i
        {
            if(v[j] >v[j+1])
            {
                ::swap(v[j],v[j+1]);
                flag = false;
            }
        }
        if(flag) break;//如果没有进入交换，就是说明已经有序了
    }
}

快速排序

思想：取待排序区间上的某一个元素作为基准值，根据处理方法，将待排序区间上的元素划分为：左区间的元素小于基准值，右区间的元素大于基准值，然后对左右区间重复这个过程，直到所有元素都排列在相应位置上为止

时间复杂度分析：

  • 最好情况： O(N*logN)
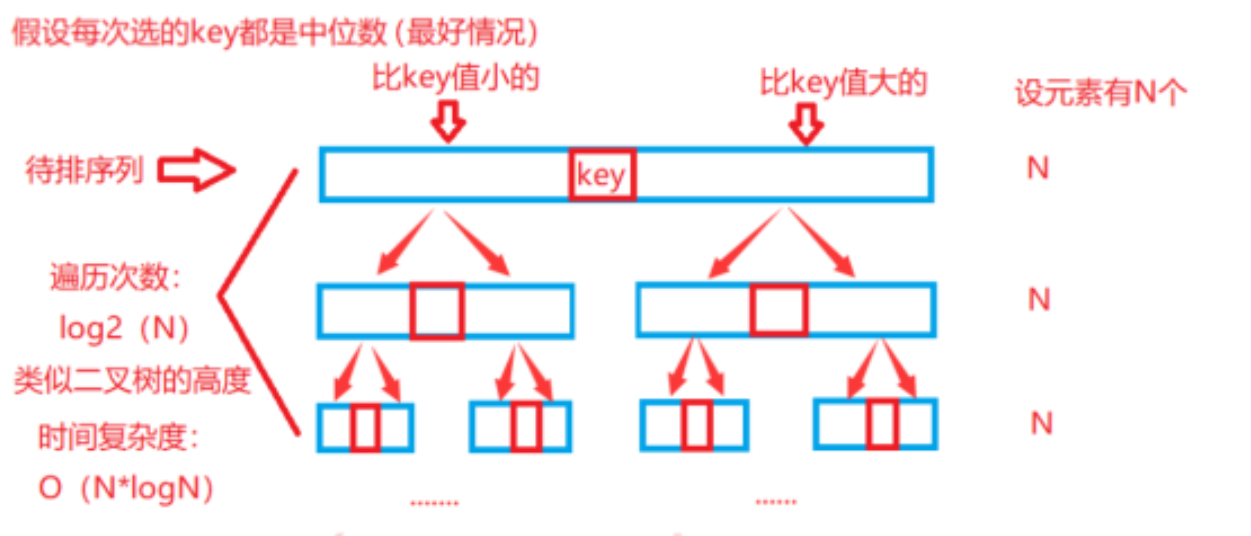
image-20220325225722992

每一层的所有左区间和右区间的单趟加起来，共处理N个元素 ，递归高度为logN 每一层处理N个元素 ，所以复杂度为N*logN

  • 最坏情况：数组是有序的 O(N^2)

因为有序时：选取的key都是左边(右边)的元素，那么每一趟排序的元素个数呈现等差数列

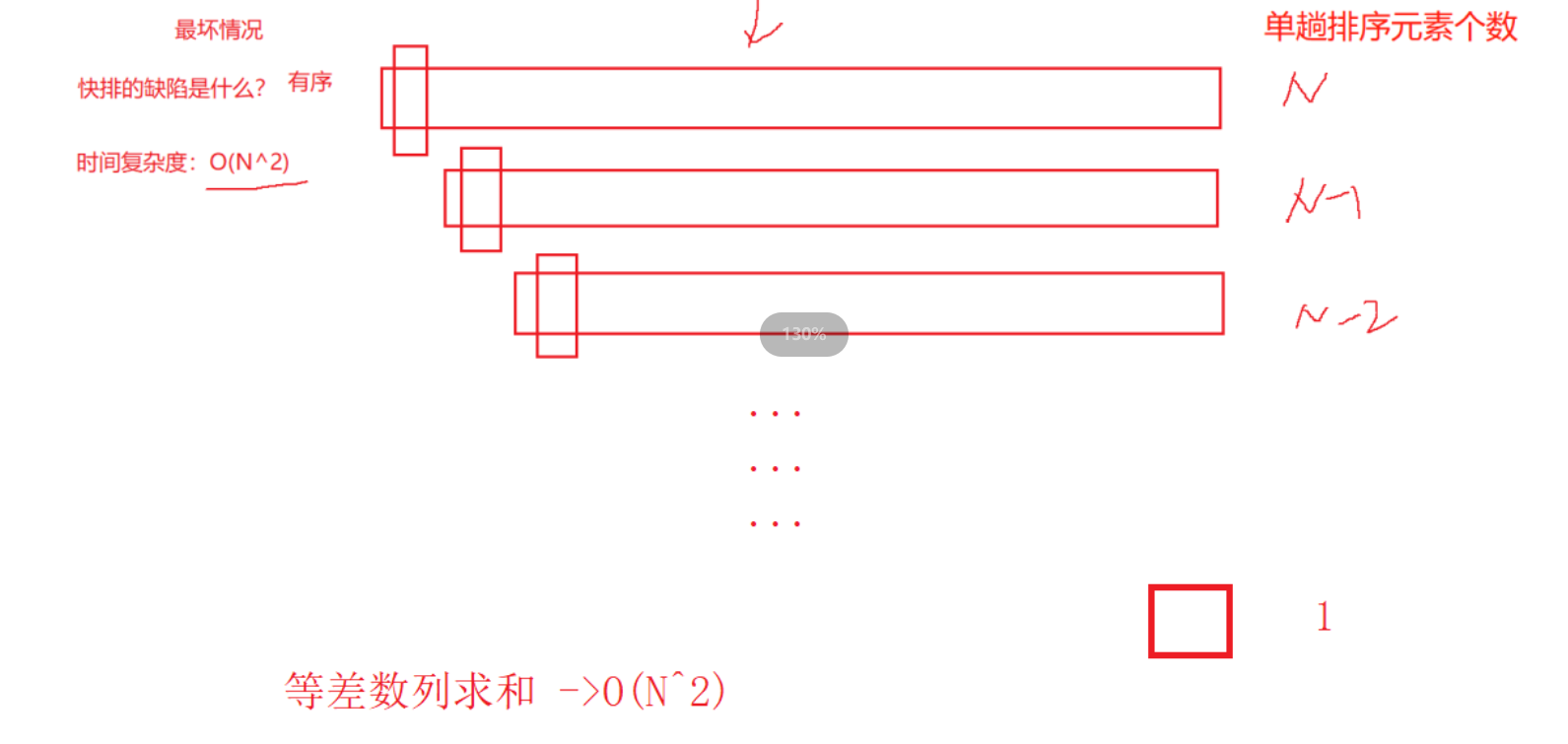
image-20220325225800206

并且有可能递归层次太深，导致栈溢出

解决办法：

  • 方法1：三数取中(左边，中间，右边，三者的中间值作为基准值)
    • 三数取中的目的：在数组有序情况下，尽量不会取到最大/最小的为基准值，提高性能，防止栈溢出
  • 方法2：随机取基准值

空间复杂度分析：

  • 快排空间复杂度：主要是递归调用栈所占用的空间，与递归深度成线性关系。

    最好情况（递归树最平衡）：O(log n)

    平均情况：O(log n)

    最坏情况（递归树最高）：O(n)

稳定性：不稳定

  • 三数取中可能会导致相对顺序改变

hoare版本

注意1：若选左边的值作为key，右边的先走。若选右边的值作为key，左边的先走

int process(vector<int>& v,int left,int right)
{
    int keyi = left;//左边的作为key  那么右边先走
    while(left < right)
    {
        //右往左走 找严格小的
        while(left < right && v[right] >= v[keyi])
            right--;
        //左往右走 找严格大的
        while(left < right && v[left] <= v[keyi])
            left++;

        if(left < right) ::swap(v[right],v[left]);
    }
    ::swap(v[left],v[keyi]); 
    return left;
}
void QucikSort(vector<int>& v,int left,int right)
{
    if(left >= right) return ;
    ::swap(v[left],v[left + rand() % (right - left + 1)]);//取左边位置作为基准值 ==> 本质是随机选key 
    int keyi = process(v,left,right);
    //[left,keyi-1] keyi[keyi+1,right]
    QucikSort(v,left,keyi-1);
    QucikSort(v,keyi+1,right);
}

挖坑法

image-20220114155908775

注意：最初要保存的key是左边元素的值，而不是下标！因为可能会被覆盖

int process(vector<int>& v,int left,int right)
{
    int keyi = v[left];//左边的作为key  那么右边先走
    int pivot = left;//坑位
    while(left < right)
    {
        //右往左走 找严格小的
        while(left < right && v[right] >= keyi)
            right--;
        ::swap(v[right],v[pivot]);
        pivot = right;//更新坑位

        //左往右走 找严格大的
        while(left < right && v[left] <= keyi)
            left++;
        ::swap(v[left],v[pivot]);
        pivot = left;//更新坑位
    }
    v[pivot] = keyi;
    return pivot;
}
void QucikSort(vector<int>& v,int left,int right)
{
    if(left >= right) return ;
    ::swap(v[left],v[left + rand() % (right - left + 1)]);//取左边位置作为基准值 ==> 本质是随机选key 
    int keyi = process(v,left,right);
    //[left,keyi-1] keyi[keyi+1,right]
    QucikSort(v,left,keyi-1);
    QucikSort(v,keyi+1,right);
}

两路划分

划分为：<=基准值的放左边，>基准值的放右边

做法：定义一个变量lessEqual表示<=基准值的区域，最初初始化为left-1 ，然后cur从left位置开始往后遍历，遍历[left,right-1]区间(因为以最右位置作为基准值)

  • 如果当前数<=基准值，那么当前数和<=区域的下一个数交换，然后<=区域向右扩展，当前数跳向下一个数
  • 如果当前数>基准值，当前数直接跳向下一个数
  • [left,lessEqual)表示<=基准值的区域 最后让基准值和lessEqual+1位置交换，然后返回该位置
int process(vector<int>& v,int left,int right)
{
    int lessEqual = left - 1;//表示<=基准值的区域
    int cur = left;
    //遍历[left,right-1]区间,以右边作为基准值
    while(cur < right)
    {
        if(v[cur] <= v[right])
            swap(v[++lessEqual],v[cur]);
        cur++; //不管怎么样,cur都要往右走
    }
    //[left,lessEqual)表示<=基准值的区域
    ::swap(v[++lessEqual],v[right]);
    return lessEqual;
}
void QucikSort(vector<int>& v,int left,int right)
{
    if(left >= right) return ;
    ::swap(v[right],v[left + rand() % (right - left + 1)]); //取右边位置作为基准值 ==> 本质是随机选key 
    int keyi = process(v,left,right);
    //[left,keyi-1] keyi[keyi+1,right]
    QucikSort(v,left,keyi-1);
    QucikSort(v,keyi+1,right);
}

快排致命点

当所有元素都一样时：快速排序非常慢->O(N^2)，此时加了三数取中也不行 或者类似是2 3 2 3 2 3 的数据

三路划分

目标：<x的放左边,=x的放中间,>x的放右边

定义两个变量：less表示<=x的区域，more表示>x的区域。以最右边作为基准值，最初less初始化为:left more初始化为right

  • [ l e f t ， l e s s ) [left，less) [left，less)表示<=x的区域 ( m o r e ， r i g h t ] (more，right] (more，right]表示>x的区域

从left位置开始往后遍历，直到与more位置相遇

步骤：

  • 1.当前数<目标数 当前数和less位置交换, 然后小于区域向右扩展, 当前数向后跳
  • 2.当前数 = 目标数 当前数直接跳到下一个数,
  • 3.当前数>目标数 当前数和more位置的数交换, 然后大于区域向左扩, 当前数停在原地,下一次继续看这个当前数
//作用：选取[left,right]的一个数为基准值
//然后把这个区间内的元素划分为: 左边<pivot  中间=pivot 右边>pivot
int* process(vector<int>& v,int left,int right,int pivot)
{
    int less = left;// <pivot的区域 [left,less)
    int more = right;// >pivot的区域 (more,right]
    int cur = left;
    //从left位置开始往后走，直到和more相遇,more位置的值也需要考察
    while(cur <= more)
    {
        if(v[cur] > pivot)
            ::swap(v[more--],v[cur]); //当前数换到大于区域当中,还要继续考察换过来的这个数
        else if(v[cur] < pivot)
            ::swap(v[less++],v[cur++]);//当前数换到小于区域当中,然后cur往后走
        else
            cur++;
    }
    //[left,less) [less,more] (more,right]
    return new int[2]{less,more};
}
void QucikSort(vector<int>& v,int left,int right)
{
    if(left >= right) return ;
    ::swap(v[right],v[left + rand() % (right - left + 1)]);
    int* equal = process(v,left,right,v[right]);
    //[left,equal[0]-1] [euqal[0],equal[1]] [euqal[1]+1,right]
    QucikSort(v,left,equal[0]-1);
    QucikSort(v,equal[1]+1,right);
}

小区间优化

小区间优化：当分割到小区间时：不再采用递归的方法让这段子区间有序， 减少递归次数

如果区间内的元素小于10了，就不使用快排进行排序，因为这段区间已经接近有序了，使用直接插入排序进行排序这区间的元素

void InsertSort_QuickSort(vector<int>& v,int left,int right)
{
    for(int i = left;i<right;i++) 
    {
        int end = i;//end的范围:[left,right-1]
        int x = v[end+1];//将x插入到[0,end]的有序区间
        while(end >= left) //注意：这里最多移动到left！！！并不是0
        {
            if(v[end] > x)
            {
                v[end+1] = v[end];
                end -= 1;
            }
            else
                break;
        }
        v[end+1] = x;
    }
}   
//作用：选取[left,right]的一个数为基准值
//然后把这个区间内的元素划分为: 左边<pivot  中间=pivot 右边>pivot
int* PartSort(vector<int>& v,int left,int right,int pivot)
{
    int less = left;// <pivot的区域 [left,less)
    int more = right;// >pivot的区域 (more,right]
    int cur = left;
    //从left位置开始往后走，直到和more相遇,more位置的值也需要考察
    while(cur <= more)
    {
        if(v[cur] > pivot)
            ::swap(v[more--],v[cur]); //当前数换到大于区域当中,还要继续考察换过来的这个数
        else if(v[cur] < pivot)
            ::swap(v[less++],v[cur++]);//当前数换到小于区域当中,然后cur往后走
        else
            cur++;
    }
    //[left,less) [less,more] (more,right]
    return new int[2]{less,more};
}
void QuickSort(vector<int>& v,int left,int right)
{
    if(left >= right)
        return ;
    if(right - left +1 < 10)
    {
        InsertSort_QuickSort(v,left,right);
    }
    else
    {
        //结合随机选数
        ::swap(v[right],v[left + rand() %(right - left + 1)]);
        //PartSort以最右边的值为划分值,返回的是 等于arr[right]的区域的范围 [equalArea[0],equalArea[1]]
        int* equalArea = PartSort(v,left,right,v[right]);
        //[left,equalArea[0]-1] [equalArea[1] + 1,right]
        QuickSort(v,left,equalArea[0]-1);
        QuickSort(v,equalArea[1]+1,right);
    }
}

快排非递归

递归的时候，栈帧里面存放的是左右区间的下标，我们可以把左右区间的下标值放到栈中

注意：

1.因为栈是后进先出的，所以如果先排序左区间再排序右区间，则要先把右区间的左右下标先进栈

2.循环结束的条件：栈为空。如果栈不为空，说明还有区间要进行处理

能过！

void QuickSortNonR(vector<int>& v,int left,int right)
{
    if(left >= right) return ;
    stack<int> st;//存储要排序的区间
    //注意：栈的特性为后进先出
    st.push(right);
    st.push(left);
    while(!st.empty()) //还有区间要排序
    {
        int begin = st.top();//左端点
        st.pop();
        int end = st.top();//右端点
        st.pop();
        if(end - begin + 1 < 10)
        {
            InsertSort_QuickSort(v,begin,end);
            continue;
        }

        ::swap(v[end],v[begin + rand() % (end - begin + 1)]);
        int* equalArea = PartSort(v,begin,end,v[end]);
        //[left,equalArea[0]-1] [equalArea[1] + 1,right]
        if(right > equalArea[1] + 1)
        {
            QuickSortNonR(v,equalArea[1]+1,right); //仍然需要递归
        }
        if(equalArea[0]-1 > left)
        {
            QuickSortNonR(v,left,equalArea[0]-1);
        }

    }
}

不能过

void Insert_Quick(vector<int>& v,int left,int right)
{
    for(int i = left;i<right;i++) //i < right!!!!
    {
        int end = i;
        int x = v[end+1];
        while(end  >= left) //坑！！ end最多移动到left位置
        {
            if(v[end] > x)
                v[end + 1 ]  = v[end],end--;
            else 
                break;
        }
        v[end + 1] = x;
    }
}
void QuickSortNonR(vector<int>& v,int left,int right)
{
    if(left>=right) return ;
    stack<int> st;
    st.push(left);
    st.push(right);
    while(!st.empty())
    {
        //栈的特性：后进先出,所以先拿到右端点
        int end = st.top();
        st.pop();
        int begin = st.top();
        st.pop();
        if(end - begin + 1 < 10)
        {
            Insert_Quick(v,begin,end);
            continue;
        }
        ::swap(v[begin],v[begin + rand() % (end - begin + 1)]);//左边作为基准值
        int keyi = PartSort(v,begin,end);
        //[begin,keyi-1] key [keyi+1,end]
        if(keyi-1 > begin)
        {
            st.push(begin);
            st.push(keyi-1);
        }
        if(end > keyi+1)
        {
            st.push(keyi+1);
            st.push(end);
        }
    }
}

归并排序

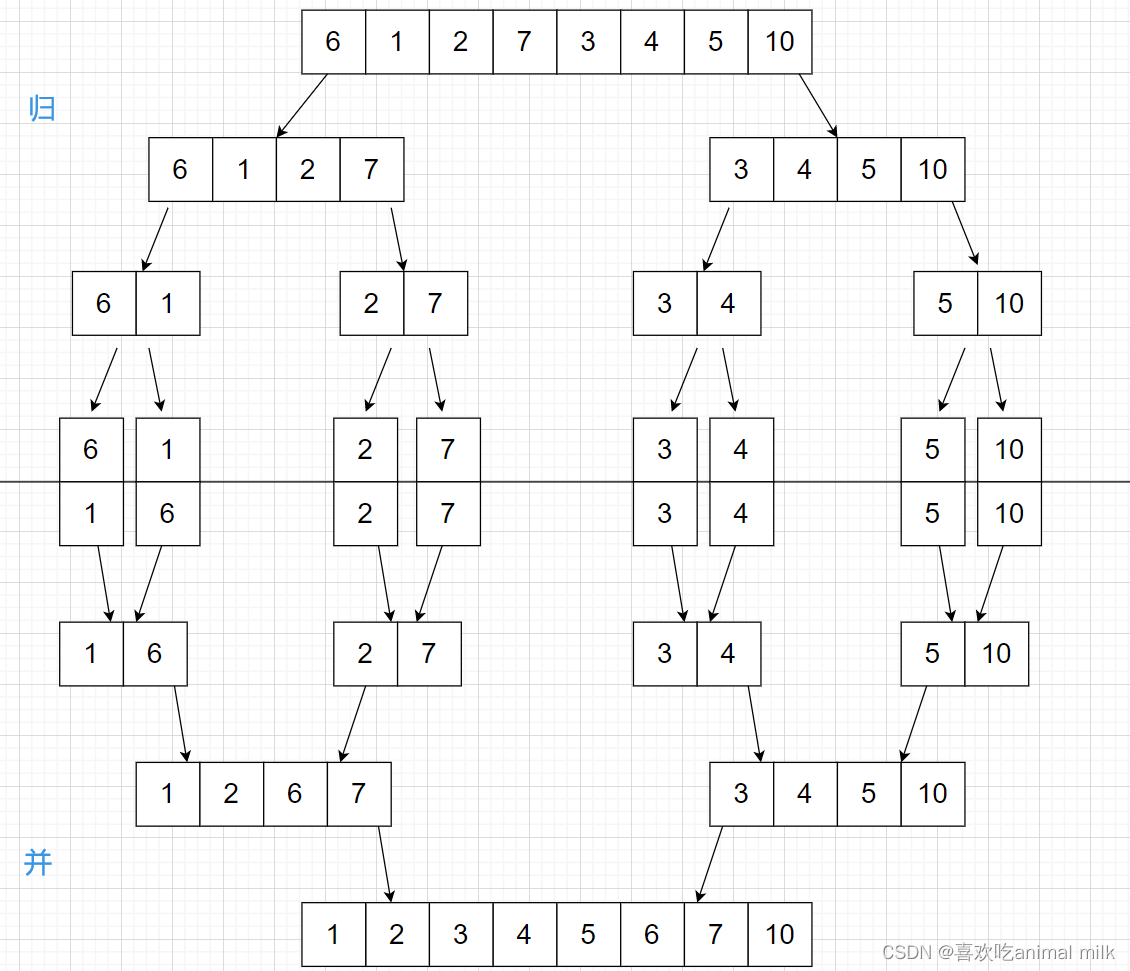
思想：根据左右区间的值，计算一个中间值mid，先让[left，mid] [mid+1，right]两个区间有序， 然后这两个有序区间进行归并 (归并到临时数组)，将临时数组的内容拷贝回去

时间复杂度：O(N*logN)

空间复杂度：O(N)

稳定性：稳定

  • 归并的时候，相同的值，先拷贝左区间的值，再拷贝右区间的
image-20220210202604866 
void MergeSort(vector<int>& v,int left,int right,vector<int>& tmp)
{
    if(left >= right)  //数组只有一个元素/区间不合法就结束
        return ;
    //求中间值：left + (right - left) / 2 或者  (left + right) >> 1
    int mid = (left + right) / 2;
    MergeSort(v,left,mid,tmp);//左区间[left,mid]排成有序
    MergeSort(v,mid+1,right,tmp);//右区间[mid+1,right]排成有序

    //左右区间进行归并
    int begin1 = left,end1 = mid,begin2 = mid+1,end2 = right;
    int index = left;//拷贝到临时数组的哪个位置
    while(begin1 <= end1 && begin2 <= end2)
    {
        //排升序,谁小拷贝谁
        if(v[begin1] > v[begin2])
            tmp[index++] = v[begin2++];
        else  //相同的时候,先拷贝左边,再拷贝右边==>稳定
            tmp[index++] = v[begin1++];
    }
    //某个区间可能还未拷贝完,继续拷贝
    while(begin1 <= end1) tmp[index++] = v[begin1++];
    while(begin2 <= end2) tmp[index++] = v[begin2++];
    //将临时数组的数据重新拷贝回去原数组,注意起始位置为left！！ [left,right]区间
    for(int i = left;i<=right;i++)
        v[i] = tmp[i];
}

非递归版本

非递归：1.改成循环的写法 2.用栈/队列模拟

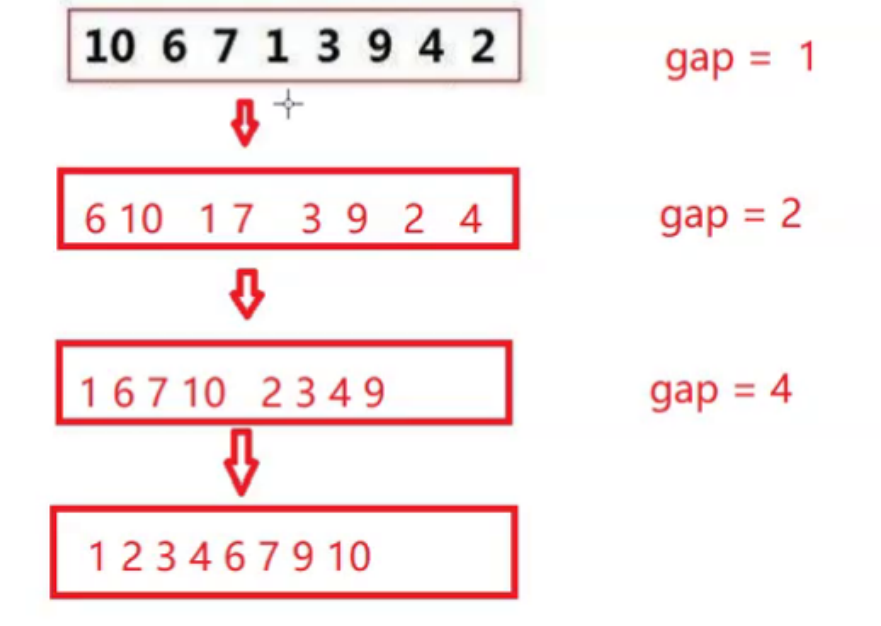
image-20220114204056815

关于gap

int gap = 1;//gap为几，就几个几个一起归并   
for(int i = 0;i<n;i += 2*gap)
{
    //[i，i+gap-1] [i+gap，i+2*gap-1]
}
gap = 1: [0，0][1，1]的为一组 ...  一个元素为一个区间，两个区间归并
gap = 2: [0，1][2，3]的为一组 ...  两个元素为一个区间，两个区间归并
gap = 4: [0，3][4，7]的为一组 ...  四个元素为一个区间，两个区间归并
//如何控制多组？->即控制gap ==>控制多次归并  11归并 22归并 44归并
int gap = 1;
while(gap < n)
{
    gap *= 2;
}

写法1：

要修正，不能使用break的根本原因：整体归并完才拷贝，把tmp数组的内容拷贝回原数组放在了循环外面，若提前break，后面越界区间的值并没有拷贝到tmp数组中，导致tmp数组再拷贝回去的值可能覆盖有越界区间的值，把随机值拷贝回去原数组.

image-20230812165617106

void MergeSortNonR(vector<int>& v)
{
    int gap = 1,n = v.size();
    vector<int> tmp(n);//辅助数组
    while(gap < n) //gap为几：几个几个元素之间归并
    {
        //推导范围:因为gap个元素作为一个区间，两个区间进行归并,所以下一轮：i+=2*gap
        //[i,i+gap-1] [i+gap,i + 2* gap - 1]
        for(int i = 0;i<n;i += 2*gap)
        {
            int begin1 = i,end1 = i+gap-1;
            int begin2 = i + gap,end2 = i+2*gap-1;

            //因为是整体归并完才拷贝
            //把tmp数组的内容拷贝回原数组放在了循环外面
            //若提前break，后面越界区间的值并没有拷贝到tmp数组中，导致tmp数组再拷贝回去的值可能覆盖有越界区间的值，把随机值拷贝回去原数组.

            if (end1 >= n)  end1 = n - 1;//end1越界,[begin2,end2]不存在
            if (begin2 >= n)//[begin2,end2]不存在
            {
                //修正成不存在的区间 begin2>end2
                begin2 = n ;
                end2 = n -1;
            }
            if (end2 >= n)//end2越界
                end2 = n - 1;

            //[begin1,end1] [begin2,end2]
            int index = i;//归并元素从tmp的哪个位置开始向后拷贝
            while(begin1 <= end1 && begin2 <= end2)
            {
                if(v[begin1] > v[begin2])
                    tmp[index++] = v[begin2++];
                else 
                    tmp[index++] = v[begin1++]; 
            }
            while(begin1 <= end1) tmp[index++] = v[begin1++];
            while(begin2 <= end2) tmp[index++] = v[begin2++];
        }
        //所有的11归并 22归并结束之后,再整体[0,n-1]区间拷贝回去
        for (int i = 0; i < n; i++)
            v[i] = tmp[i];
        gap *= 2;
    }
}

写法2：归并一部分，拷贝一部分回去

对于此时：[begin1，end1] [begin2，end2]

  • end1越界了：不需要处理了，从begin1开始，后面区间的元素不需要归并，已经在原数组里面了
  • begin2越界：不需要处理了，只有[begin1，end1]区间元素有效，一个区间不需要归并，元素已经在原数组里面了
  • 若：end2越界->需要归并，因为两个需要归并的区间里面都有值->要修正end2的位置==> end2= n - 1 ，end2越界，则第二个区间至少有一个值
void MergeSortNonR(vector<int>& v)
{
    int gap = 1,n = v.size();
    vector<int> tmp(n);//辅助数组
    while(gap < n) //gap为几：几个几个元素之间归并
    {
        //推导范围:因为gap个元素作为一个区间，两个区间进行归并,所以下一轮：i+=2*gap
        //[i,i+gap-1] [i+gap,i + 2* gap - 1]
        for(int i = 0;i<n;i += 2*gap)
        {
            int begin1 = i,end1 = i+gap-1;
            int begin2 = i + gap,end2 = i+2*gap-1;
            //由于是归并一部分，然后拷贝一部分回去,所以如果某一个区间越界了,那么本轮就不需要归并了
            if(begin1 >=n || begin2 >= n) break;
            if(end2 >= n) end2 = n-1;//修正结束位置

            //[begin1,end1] [begin2,end2]
            int index = i;//归并元素从tmp的哪个位置开始向后拷贝
            while(begin1 <= end1 && begin2 <= end2)
            {
                if(v[begin1] > v[begin2])
                    tmp[index++] = v[begin2++];
                else 
                    tmp[index++] = v[begin1++]; 
            }
            while(begin1 <= end1) tmp[index++] = v[begin1++];
            while(begin2 <= end2) tmp[index++] = v[begin2++];

            //拷贝回去原数组 区间为:[i(begin1),end2] 
            //由于begin1已经改变,所以要使用i变量
            for(int j = i;j<=end2;j++)
            {
                v[j] =  tmp[j];
            }
        }
        gap *= 2;
    }
}

计数排序-鸽巢原理

主要思想：统计相同元素出现次数，根据统计的结果将序列写回到原来的序列中

绝对映射

把要排序数组的值放到count对应下标位置

缺点：空间消耗大.而且针对负数也不好解决

void CountSort(vector<int>& v)
{
    int n = v.size();
    //1.找出数组的最大值
    int maxNum = v[0];
    for(int i = 1;i<n;i++)
        if(v[i] > maxNum) maxNum = v[i];
    //2.每个元素映射到count数组的对应位置
    vector<int> count(maxNum+1,0);//注意要开maxNum+1个空间！
    for(auto& x:v)
        count[x]++;
    //3.将count数组的内容映射回去原数组
    int index = 0;
    for(int i = 0;i<=maxNum;i++) //注意:i<=maxNum
    {
        while(count[i] > 0)//元素i的出现次数为count[i]
        {
            v[index++] = i;
            count[i]--;//i元素出现次数--,否则死循环
        }
    }
}

相对映射

找出要排序数组的最大值和最小值，开max - min + 1个空间： [min，max]元素个数就是max - min + 1。将元素映射在count数组的位置是: a[i] - min位置， 到时候放回去原数组的值是:a[i] + min

  • 针对负数也很好处理
void CountSort(vector<int>& v)
{
    int n = v.size();
    //1.找出数组的最大值
    int maxNum = v[0];
    int minNum = v[0];
    for(int i = 1;i<n;i++)
    {
        if(v[i] > maxNum) maxNum = v[i];
        if(v[i] < minNum) minNum = v[i];
    }
    int range = maxNum - minNum + 1;//数组元素范围:[minNum,maxNum]
    //2.数组元素进行映射。此时x元素映射在x - minNum位置
    vector<int> count(range,0);
    for(auto& x:v)
        count[x - minNum]++;
    //3.将count数组的内容映射回去原数组,此时对应的值为i + minNum
    int index = 0;
    for(int i = 0;i< range;i++)
    {
        while(count[i] > 0)//元素i的出现次数为count[i]
        {
            v[index++] = i + minNum;
            count[i]--;//i元素出现次数--,否则死循环
        }
    }
}

时间复杂度：O(MAX(N，范围))

空间复杂度：O(范围)

稳定性：不稳定

  • 计数到count数组中,每个元素已经没有顺序了

插入排序和选择排序的对比

横向对比：

  • 直接选择排序最差，因为无论什么场景下都是O(N^2)
  • 直接插入排序和冒泡排序，最坏都是O(N^2)，最好都是O(N)

对于已经有序的数组排序，直接插入和冒泡排序效率一样高，然而对接近有序数组，直接插入排序更好，需要的比较次数更少一点，所以后续的快速排序小区间优化使用的就是直接插入排序

  • 因为冒泡一次之后，数组变成有序(比较n-1次)， 但是还要再冒泡一次(比较n-2次)发现没有交换的机会，flag = 1->跳出循环

总结

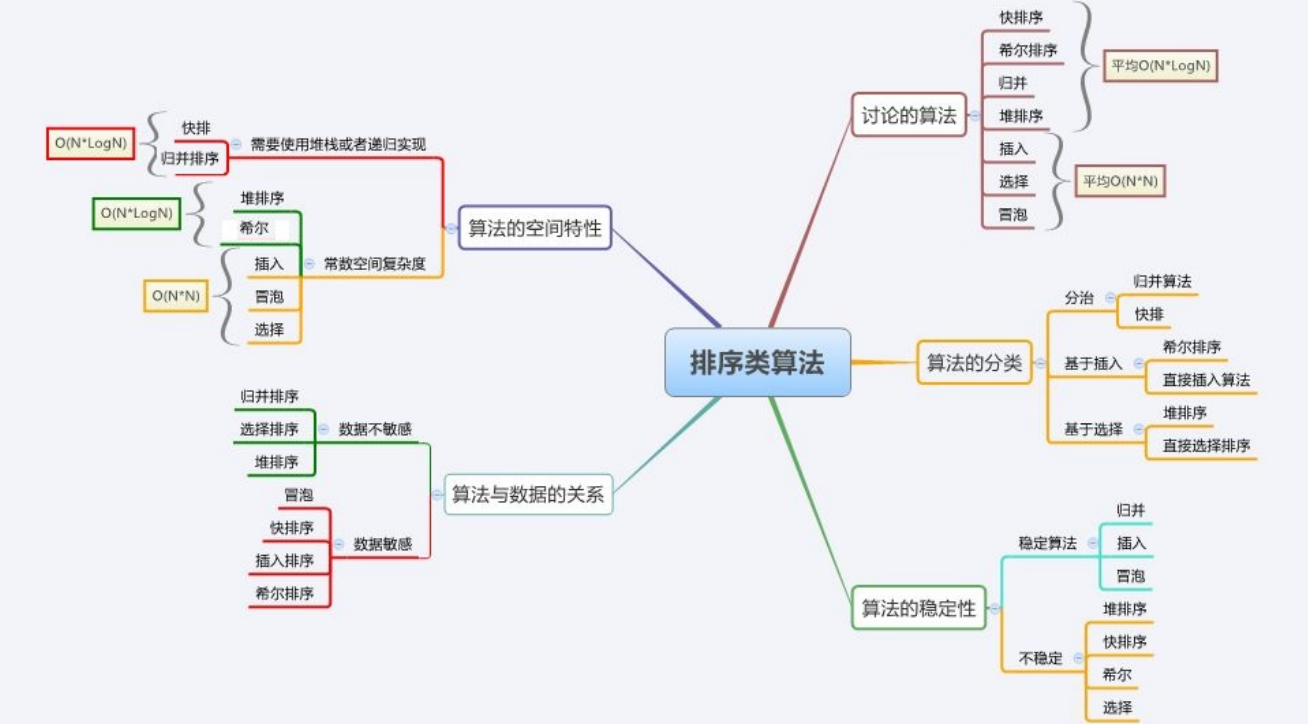
image-20220114200328313

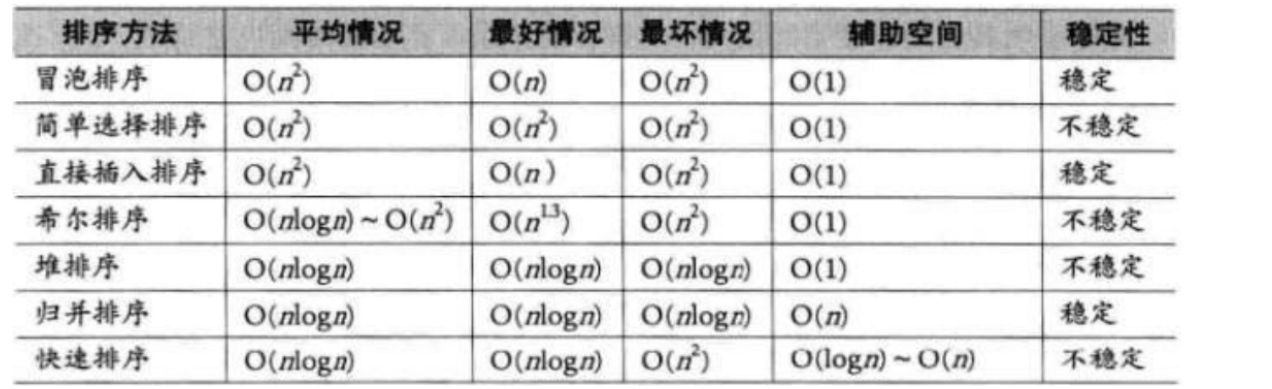
image-20220314211414535

注意：

1.对于快速排序:如果加了三数取中 + 三路归并 最坏就不是O(N^2)

2.为了绝对的速度选快排，为了省空间选堆排，为了稳定性选归并

3.时间复杂度:O(N*logN)，额外空间复杂度低于O(N)，且稳定的基于比较的排序是不存在的

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1046221.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

UNITY—2D游戏制作入门！

UNITY—2D游戏制作入门！

Unity作为当今最流行的游戏引擎之一&#xff0c;受到各大厂商的喜爱。 像是炉石传说&#xff0c;以及逃离塔克夫&#xff0c;都是由unity引擎开发制作。 作为初学者的我们&#xff0c;虽然无法直接做出完成度那么高的作品&#xff0c;但每一个伟大的目标&#xff0c;都有一个…
阅读更多...
机柜PDU产品采购与安装指南——TOWE精选

机柜PDU产品采购与安装指南——TOWE精选

机柜PDU指的是Power Distribution Unit&#xff0c;即电源分配单元。它是一种电子设备&#xff0c;通常用于为数据中心、服务器机房等设施中的计算机和其他设备提供电力&#xff0c;是各行业数据中心“标配”构成部分&#xff0c;以确保服务器等用电设备的安全和稳定运行。 数据…
阅读更多...
Android的GNSS功能，搜索卫星数量、并获取每颗卫星的信噪比

Android的GNSS功能，搜索卫星数量、并获取每颗卫星的信噪比

一、信噪比概念 信噪比&#xff0c;英文名称叫做SNR或S/N&#xff08;SIGNAL-NOISE RATIO)&#xff0c;又称为讯噪比。是指一个电子设备或者电子系统中信号与噪声的比例。 信噪比越大&#xff0c;此颗卫星越有效&#xff08;也就是说可以定位&#xff09;。也就是说&#xff0…
阅读更多...
2023最新最详细软件测试技术面试题【含答案】

2023最新最详细软件测试技术面试题【含答案】

【软件测试面试突击班】如何逼自己一周刷完软件测试八股文教程&#xff0c;刷完面试就稳了&#xff0c;你也可以当高薪软件测试工程师&#xff08;自动化测试&#xff09; 有这样一个面试题&#xff1a;在一个Web测试页面上&#xff0c;有一个输入框&#xff0c;一个计数器&…
阅读更多...
【考研数学】概率论与数理统计 —— 第三章 | 二维随机变量及其分布（3，二维随机变量函数的分布）

【考研数学】概率论与数理统计 —— 第三章 | 二维随机变量及其分布（3，二维随机变量函数的分布）

文章目录 七、二维随机变量函数的分布7.1 二维随机变量函数分布的基本情形 ( X , Y ) (X,Y) (X,Y) 为二维离散型随机变量 ( X , Y ) (X,Y) (X,Y) 为二维连续型随机变量 X X X 为离散型变量&#xff0c; Y Y Y 为连续型变量 7.2 常见二维随机变量的函数及其分布 Z min ⁡ { X ,…
阅读更多...
使用“讯飞星火”快速生成高质量PPT文档

使用“讯飞星火”快速生成高质量PPT文档

随着互联网的发展,人们获取信息的渠道越来越多,如何在有限的时间内快速完成工作任务变得尤为重要。在此背景下,各类智能写作工具应运而生。讯飞星火(https://xinghuo.xfyun.cn/desk)就是这样一款非常实用的工具。它能够通过AI技术,仅需输入标题、关键词等信息,就能快速生成完整…
阅读更多...
从零学算法（LCR 191）

从零学算法（LCR 191）

为了深入了解这些生物群体的生态特征&#xff0c;你们进行了大量的实地观察和数据采集。数组 arrayA 记录了各个生物群体数量数据&#xff0c;其中 arrayA[i] 表示第 i 个生物群体的数量。请返回一个数组 arrayB&#xff0c;该数组为基于数组 arrayA 中的数据计算得出的结果&am…
阅读更多...
基于MAC地址划分VLAN实验

基于MAC地址划分VLAN实验

背景 随着互联网迅速发展，及电脑终端的小型化，企业移动化办公需求日益增加。 传统的基于接口划分VLAN已不能满足移动办公环境下位置变化导致终端所在子网变化，从而影响企业员工固定ip的终端位置移动后不能正常获取原IP；另一方面也影响网络安全，如部门之间子网不能互通，…
阅读更多...
Kafka快速实战以及基本原理详解

Kafka快速实战以及基本原理详解

文章目录 1、Kafka介绍1.1、MQ的作用1.2、为什么要用Kafka 2、Kafka快速上手2.1、实验环境2.2、单机服务体验2.3、理解Kakfa的消息传递机制 1、Kafka介绍 ​ ChatGPT对于Apache Kafka的介绍&#xff1a; Apache Kafka是一个分布式流处理平台&#xff0c;最初由LinkedIn开发并于…
阅读更多...
Android studio升级Giraffe | 2022.3.1 Patch 1踩坑

Android studio升级Giraffe | 2022.3.1 Patch 1踩坑

这里写自定义目录标题 not "opens java.io" to unnamed module错误报错信息解决 superclass access check failed: class butterknife.compiler.ButterKnifeProcessor$RScanner报错报错信息解决 Android studio升级Giraffe | 2022.3.1 Patch 1后&#xff0c;出现项目…
阅读更多...
架构案例-架构真题2016（四十）

架构案例-架构真题2016（四十）

&#xff08;2016&#xff09;嵌入式处理器是嵌入式系统的核心部件&#xff0c;一般可分为嵌入式微处理器&#xff08;MPU&#xff09;微控制器&#xff08;MCU&#xff09;、数字信号处理器&#xff08;DSP&#xff09;和片上系统&#xff08;SOC&#xff09;。以下叙述中&…
阅读更多...
Python函数绘图与高等代数互融实例(七): 极限图|气泡图|棉棒图

Python函数绘图与高等代数互融实例(七): 极限图|气泡图|棉棒图

Python函数绘图与高等代数互融实例(一):正弦函数与余弦函数 Python函数绘图与高等代数互融实例(二):闪点函数 Python函数绘图与高等代数互融实例(三):设置X|Y轴|网格线 Python函数绘图与高等代数互融实例(四):设置X|Y轴参考线|参考区域 Python函数绘图与高等代数互融实例(五…
阅读更多...
第十四届蓝桥杯大赛软件赛决赛 C/C++ 大学 B 组 试题 C: 班级活动

第十四届蓝桥杯大赛软件赛决赛 C/C++ 大学 B 组 试题 C: 班级活动

[蓝桥杯 2023 国 B] 班级活动 【问题描述】 小明的老师准备组织一次班级活动。班上一共有 n n n 名&#xff08; n n n 为偶数&#xff09;同学&#xff0c;老师想把所有的同学进行分组&#xff0c;每两名同学一组。为了公平&#xff0c;老师给每名同学随机分配了一个 n n …
阅读更多...
33.栈，队列练习题（王道2023数据结构第3章综合应用）

33.栈，队列练习题（王道2023数据结构第3章综合应用）

试题1&#xff08;3.1.4节题3&#xff09;&#xff1a; 假设以 I 和 O 分别表示入栈和出栈操作。栈的初态和终态均为空&#xff0c;入栈和出栈的操作序列可表示为仅有 I 和 O 组成的序列&#xff0c;可以操作的序列为合法序列&#xff0c;否则称为非法序列。 &#xff08;1&a…
阅读更多...
C++——namespace std

C++——namespace std

命名空间&#xff08;namespace&#xff09; 0.使用方法 namespace 命名空间名 {... } 1. 每个命名空间都是一个作用域 同其他作用域类似&#xff0c;命名空间中的每个名字都必须表示该空间内的唯一实体。因为不同命名空间的作用域不同&#xff0c;所以在不同命名空间内可以…
阅读更多...
Neural Insights for Digital Marketing Content Design 阅读笔记

Neural Insights for Digital Marketing Content Design 阅读笔记

KDD-2023 很值得读的文章&#xff01; 1 摘要 电商里&#xff0c;营销内容的实验&#xff0c;很重要。 然而&#xff0c;创作营销内容是一个手动和耗时的过程&#xff0c;缺乏明确的指导原则。 本文通过 基于历史数据的AI驱动的可行性洞察&#xff0c;来弥补 营销内容创作 和…
阅读更多...
96 # cookie

96 # cookie

cookie 和 session 和 sessionStorage 和 localStorage localStorage 和 sessionStorage 本地储存&#xff08;发送请求不会携带&#xff09;&#xff0c;不能跨域localStorage 浏览器关闭后不会清空&#xff0c;必须手动清空sessionStorage 浏览器关闭后就会销毁http 无状态的…
阅读更多...
【Vue】条件渲染列表渲染来啦

【Vue】条件渲染列表渲染来啦

hello&#xff0c;我是小索奇哈&#xff0c;精心制作的Vue系列持续发放&#xff0c;涵盖大量的经验和示例&#xff0c;由浅入深进行讲解。 本章给大家讲解的是条件&列表渲染&#xff0c;前面的章节已经更新完毕&#xff0c;后面的章节持续输出&#xff0c;有任何问题都可以…
阅读更多...
Anaconda启动错误

Anaconda启动错误

错误 An unexpected error occurred on Navigator start-up | Could not find a suitable TLS CA certificate bundle, invalid path 导致Anaconda启动失败&#xff01; [解决办法]1 找到anaconda的安装目录&#xff0c;该目录下的__init__.py 这两处分别改为verifyself.sessio…
阅读更多...
程序员不得不知道的排序算法-上

程序员不得不知道的排序算法-上

目录 前言 1.冒泡排序 2.选择排序 3.插入排序 4.希尔排序 5.快速排序 6.归并排序 总结 前言 今天给大家讲一下常用的排序算法 1.冒泡排序 冒泡排序&#xff08;Bubble Sort&#xff09;是一种简单的排序算法&#xff0c;它重复地从待排序的元素中比较相邻的两个元素&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023