文章目录
- 七、二维随机变量函数的分布
- 7.1 二维随机变量函数分布的基本情形
- 7.2 常见二维随机变量的函数及其分布
- 写在最后
七、二维随机变量函数的分布
7.1 二维随机变量函数分布的基本情形
设 ( X , Y ) (X,Y) (X,Y) 为二维随机变量,以 X , Y X,Y X,Y 为变量所构成的二元函数 Z = φ ( X , Y ) Z=\varphi(X,Y) Z=φ(X,Y) ,称为随机变量 ( X , Y ) (X,Y) (X,Y) 的函数,其分布一般有如下几种情形:
( X , Y ) (X,Y) (X,Y) 为二维离散型随机变量
设 ( X , Y ) (X,Y) (X,Y) 联合分布律为 P { X = x i , Y = y j ) = p i j P\{X=x_i,Y=y_j)=p_{ij} P{X=xi,Y=yj)=pij ,则 Z = φ ( X , Y ) Z=\varphi(X,Y) Z=φ(X,Y) 的分布律如下: Z ∼ ( φ ( x 1 , y 1 ) φ ( x 1 , y 2 ) ⋯ φ ( x m , y 1 ) ⋯ p 11 p 12 ⋯ p m 1 ⋯ ) , Z\sim \begin{pmatrix} \varphi(x_1,y_1) & \varphi(x_1,y_2) & \cdots & \varphi(x_m,y_1) & \cdots\\ p_{11} & p_{12} & \cdots & p_{m1} & \cdots \end{pmatrix}, Z∼(φ(x1,y1)p11φ(x1,y2)p12⋯⋯φ(xm,y1)pm1⋯⋯), 相同的取值需要合并。
( X , Y ) (X,Y) (X,Y) 为二维连续型随机变量
设 ( X , Y ) (X,Y) (X,Y) 联合密度函数为 f ( x , y ) f(x,y) f(x,y) 。
(1)当 Z = φ ( X , Y ) Z=\varphi(X,Y) Z=φ(X,Y) 为离散型时
求出 Z Z Z 的所有可能取值,再求出其对应的概率。
(2)当 Z = φ ( X , Y ) Z=\varphi(X,Y) Z=φ(X,Y) 为连续型时
首先计算 Z Z Z 的分布函数 F Z ( z ) = P { Z ≤ z } = ∬ φ ( x , y ) ≤ z f ( x , y ) d x d y F_Z(z)=P\{Z\leq z\}=\iint_{\varphi(x,y)\leq z}f(x,y)dxdy FZ(z)=P{Z≤z}=∬φ(x,y)≤zf(x,y)dxdy ,那么 Z Z Z 的密度函数为: f Z ( z ) = { F Z ′ ( z ) , z 为可导点 0 , z 为不可导点 f_Z(z)=\begin{cases} F'_Z(z),&z为可导点 \\ 0,&z为不可导点 \end{cases} fZ(z)={FZ′(z),0,z为可导点z为不可导点
X X X 为离散型变量, Y Y Y 为连续型变量
给出 X X X 的分布律, Y Y Y 的概率密度,求 Z = φ ( X , Y ) Z=\varphi(X,Y) Z=φ(X,Y) 的分布时,一般用全概率公式。
若 X ∼ ( x 1 x 2 ⋯ x n p 1 p 2 ⋯ p n ) , X\sim \begin{pmatrix} x_1 & x_2 & \cdots & x_n \\ p_{1} & p_2 & \cdots & p_{n} \end{pmatrix}, X∼(x1p1x2p2⋯⋯xnpn), Y Y Y 的边缘密度为 f Y ( y ) f_Y(y) fY(y) ,则有 F Z ( z ) = P { φ ( X , Y ) ≤ z } = P { X = x 1 , φ ( x 1 , Y ) ≤ z } + P { X = x 2 , φ ( x 2 , Y ) ≤ z } F_Z(z)=P\{\varphi(X,Y)\leq z\}=P\{X=x_1,\varphi(x_1,Y)\leq z\}+P\{X=x_2,\varphi(x_2,Y)\leq z\} FZ(z)=P{φ(X,Y)≤z}=P{X=x1,φ(x1,Y)≤z}+P{X=x2,φ(x2,Y)≤z} + ⋯ + P { X = x n , φ ( x n , Y ) ≤ z } . +\cdots+P\{X=x_n,\varphi(x_n,Y)\leq z\}. +⋯+P{X=xn,φ(xn,Y)≤z}.
7.2 常见二维随机变量的函数及其分布
Z = min { X , Y } Z=\min\{X,Y\} Z=min{X,Y} 的分布
F Z ( z ) = P { Z ≤ z } = 1 − P { Z > z } = P { X > z , Y > z } = 1 − ∬ x > z , y > z f ( u , v ) d u d v F_Z(z)=P\{Z\leq z\}=1-P\{Z>z\}=P\{X>z,Y>z\}=1-\iint_{x>z,y>z}f(u,v)dudv FZ(z)=P{Z≤z}=1−P{Z>z}=P{X>z,Y>z}=1−∬x>z,y>zf(u,v)dudv ,特别地,当 X , Y X,Y X,Y 相互独立时,有 F Z ( z ) = 1 − [ 1 − F X ( z ) ] [ 1 − F Y ( z ) ] F_Z(z)=1-[1-F_X(z)][1-F_Y(z)] FZ(z)=1−[1−FX(z)][1−FY(z)] 。
这个变换还是比较巧妙的,同样这也提示我们,对于这类求最大最小的分布,可以去做类似处理。
Z = max { X , Y } Z=\max\{X,Y\} Z=max{X,Y} 的分布
F Z ( z ) = P { Z ≤ z } = P { X ≤ z , Y ≤ z } = ∫ − ∞ z d x ∫ − ∞ z f ( x , y ) d y F_Z(z)=P\{Z\leq z\}=P\{X\leq z,Y\leq z\}=\int_{-\infty}^zdx\int_{-\infty}^zf(x,y)dy FZ(z)=P{Z≤z}=P{X≤z,Y≤z}=∫−∞zdx∫−∞zf(x,y)dy ,特别地,当 X , Y X,Y X,Y 独立时,有 F Z ( z ) = F X ( z ) F Y ( z ) . F_Z(z)=F_X(z)F_Y(z). FZ(z)=FX(z)FY(z).
Z = X + Y Z=X+Y Z=X+Y 的分布
F Z ( z ) = P { X + Y ≤ z } = ∬ x + y ≤ z f ( x , y ) d x d y . F_Z(z)=P\{X+Y\leq z\}=\iint_{x+y\leq z}f(x,y)dxdy. FZ(z)=P{X+Y≤z}=∬x+y≤zf(x,y)dxdy.
Z = X Y Z=XY Z=XY 的分布

Z = Y X Z=\frac{Y}{X} Z=XY 的分布
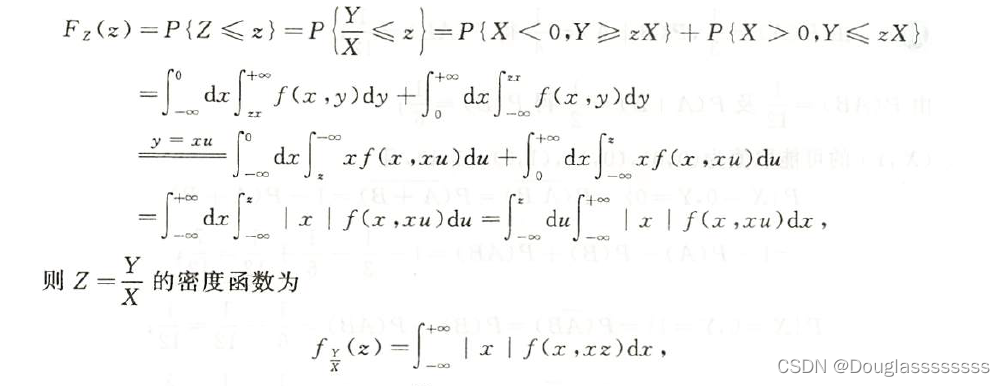
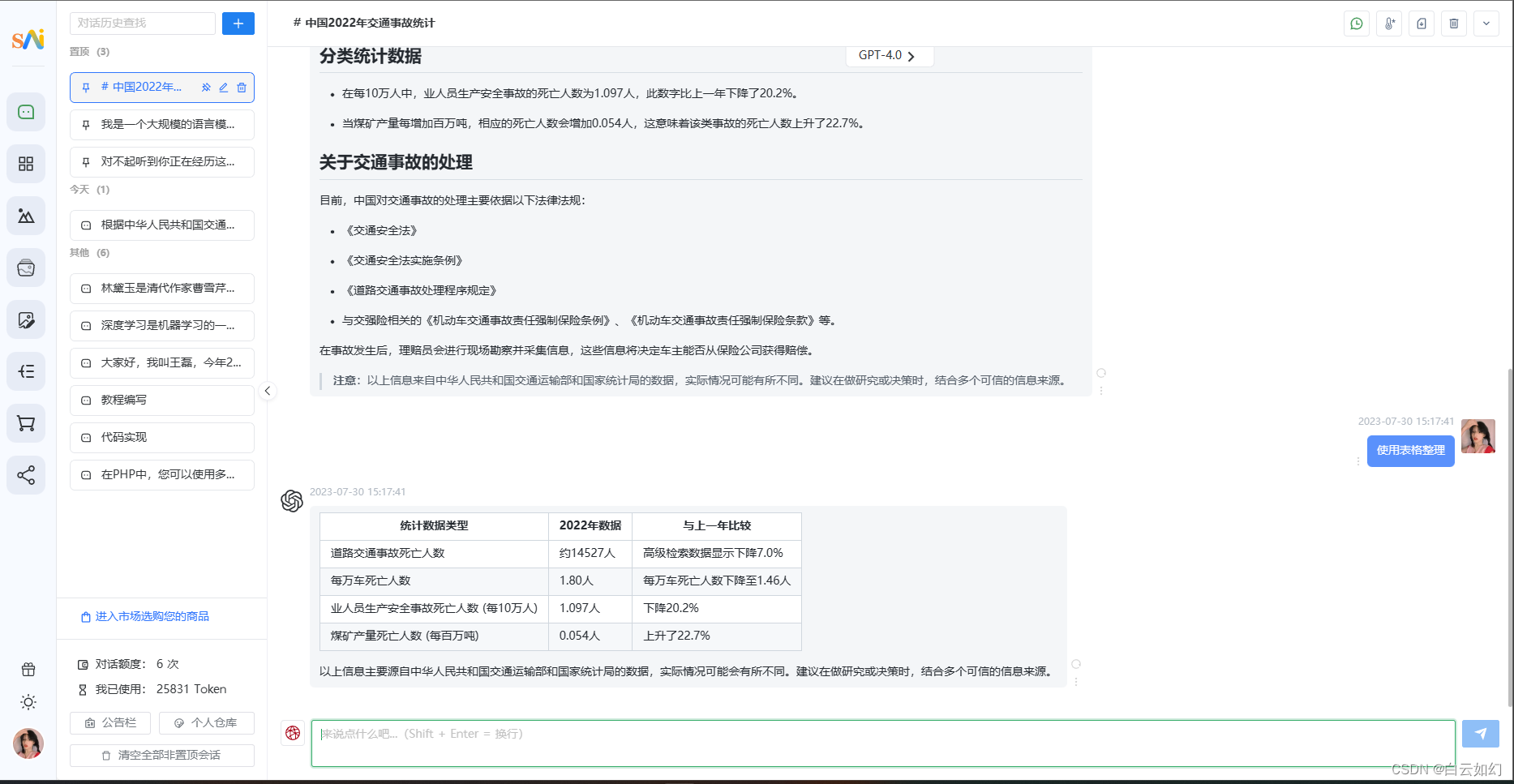
下面给出一些常见的二维随机变量的函数分布:
设 X , Y X,Y X,Y 独立,则:
(1)若 X ∼ B ( m , p ) , Y ∼ B ( n , p ) X\sim B(m,p),Y\sim B(n,p) X∼B(m,p),Y∼B(n,p) ,则 X + Y ∼ B ( m + n , p ) . X+Y \sim B(m+n,p). X+Y∼B(m+n,p).
(2)若 X ∼ P ( λ 1 ) , Y ∼ P ( λ 2 ) X\sim P(\lambda_1),Y\sim P(\lambda_2) X∼P(λ1),Y∼P(λ2) ,则 X + Y ∼ P ( λ 1 + λ 2 ) . X+Y \sim P(\lambda_1+\lambda_2). X+Y∼P(λ1+λ2).
写在最后
那到此,二维随机变量的理论内容就结束啦,掌握一维随机变量,再加上高数的二重积分的基础,这一章应该就问题不大。