1-1
一棵有124个结点的完全二叉树,其叶结点个数是确定的。T
解析:
一棵124个叶节点的完全二叉树,假设n0为叶子节点数,n1为度为1结点数,n2为度为2结点数,则有总结点数为n0+n1+n2;而n2=n0-1=123;且完全二叉树中度为1的结点只能为1个或0个,所以总结点数为124+1+123=248个
1-2
二叉树中序线索化后,不存在空指针域。 F
解析:
第一个结点无前驱,最后一个结点无后继。
1-3
对N(≥2)个权值均不相同的字符构造哈夫曼树,则树中任一非叶结点的权值一定不小于下一层任一结点的权值。T
解析:
因为中间结点的权值是下面结点的和
1-4
哈夫曼编码是一种最优的前缀码。对一个给定的字符集及其字符频率,其哈夫曼编码不一定是唯一的,但是每个字符的哈夫曼码的长度一定是唯一的。F
解析:
哈夫曼字符的频率相同时每个字符的码长不是确定的。
1-5
对于一个有N个结点、K条边的森林,不能确定它共有几棵树。F
解析:
边确定了,一个边涉及两个结点,N个结点-(k/2)就是树的棵树了。
1-6
树的后根序遍历序列等同于它所对应二叉树的中序遍历序列。 T
解析:
一棵树的后根遍历与这棵树所对应的二叉树的中序遍历相同。因为树转化为二叉树之后是没有右子树的,所以最后访问的是树的根结点。
1-7
二叉树可以用二叉链表存储,树无法用二叉链表存储。 F
解析:
二叉树与树都可以用二叉链表作为存储结构,二者的关系是一棵树可以唯一对应一棵二叉树。
1-8
将一棵树转成二叉树,根结点没有左子树。 F
解析:
左孩子右兄弟,应该是没有右兄弟,是没有右子树。
1-9
用邻接矩阵法存储图,占用的存储空间数只与图中结点个数有关,而与边数无关。T
解析:
二维矩阵,点确定了,内存就确定了。
1-10
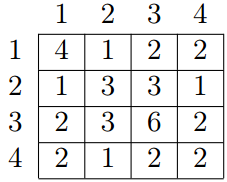
用一维数组G[]存储有4个顶点的无向图如下:
G[] = { 0, 1, 0, 1, 1, 0, 0, 0, 1, 0 }
则顶点2和顶点0之间是有边的。T
解析:
如图所示