题意：

给定两个字符串 $1\le |s_1|,|s_2|\le 5000$ ，求最短的满足各只出现一次的连续公共字串。

思路：写了个哈希超时了，哈希表常数还是太大，时限紧最好别用库内哈希表。

后缀数组解法：见 题解 。

AC代码：https://codeforces.com/contest/427/submission/181166321

题意：

构造长度为 $n,m$ 的两个字符串 $s_1,s_2$ ，使得 $s_k$ 含有 $x$ 个子串 $\text{AC}$ 。字符串递推式 $s_i=s_{i-2}+s_{i-1}$ 。

$3\le k\le 50,0\le x\le 10^9,1\le n,m\le 100$

思路：首先，递推出来 $s_k$ 有多少个 $s_1,s_2$ ，以及有多少个 $s_1{s}_2,s_2{s}_2,s_2{s}_1(s_1,s_1是没有的)$ 的连接个数。

然后就是暴力枚举 + 暴力讨论了。枚举两个字符串的首字符，尾字符，有多少个 $\text{AC}$ 暴力讨论即可。

AC代码：https://codeforces.com/contest/379/submission/181171146

构造题 ${}^{\ast }1700{\sim }^{\ast }2000$ ：

题意：

有一个长度为$n(1\le n\le 500)$的数列$a$，它可以生成一个$n\ast n$的数表，数表的第$i$行第$j$列存放的数字是$\gcd (a[i],a[j])$ （即$a[i]$和$a[j]$的最大公因数）。

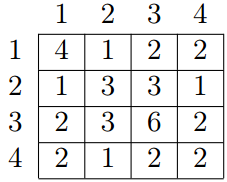
举个例子，上面那个表，就是由数列 a [ ] = { 4 , 3 , 6 , 2 } a[]=\{4,3,6,2\} a[]={4,3,6,2}生成的。

现在我们要做这样一件事情：将这个数表中的这$n\ast n$ 个数打乱，得到一个长度为$n\ast n$的序列(可参考样例1)。在已知这个序列的情况下，请还原出数列$a$。

题解：CF582A GCD Table 题解

思路：需要注意到

1. $\gcd (x,y)\le \min (x,y)$ ，也就是两个数字产生的影响是小于两个数字的。

2. 乱序序列的最大次大值一定是原序列的最大次大值。

这样的话，每次从乱序序列拿出最大值，然后和已拿出的数字计算一下，抵消掉乱序序列的影响，划归为子问题。

AC代码：https://codeforces.com/contest/582/submission/181179199

题意：

• 给定两个序列 $a$ 和 $b$，其中序列 $a$ 的长度为 $n$，序列 $b$ 的长度为 $m$。
• 分别保证序列中所有数字的最大公约数为 $1$。即 $\gcd (a_0,a_1\dots a_{n-1})=1$，$\gcd (b_0,b_1,\dots b_{m-1})=1$。
• 设 $a$ 与 $b$ 卷积的结果为序列 $c$。即 $c_k=\sum _{0\le i\le k\wedge i<n\wedge k-i<m}{a}_i\times b_{k-i}$。
• 给出一个 质数 $p$，请你求出一个下标 $t$，满足 $c_t$ 不能被 $p$ 整除。如果有多个满足要求的 $t$，请任意输出一个。
• $1\le n,m\le 10^6$，$1\le p,a_i,b_i\le 10^9$。

思路：注意到，卷积的话，两个指针的方向是相反的。如果 $a$ 的一段前缀的元素都是 $p$ 的倍数，那么这个数不管和哪个 $b$ 的元素卷一起，都还是 $p$ 的倍数。于是答案就是各找到第一个非 $p$ 的倍数，即为答案。

AC代码：https://codeforces.com/contest/1316/submission/181184451

题意：

单极磁铁，顾名思义，就是只有一个磁极（N 或 S）的磁铁，他们在实际生活中是不存在的，不过……不要在意那些细节。

我们有一个 $n$ 行 $m$ 列的方格图，要在里面放一些单极磁铁，你可以随便放置，甚至把多个磁铁放在同一个格子里。

单极磁铁的吸引是这么定义的：任选一个 N 极磁铁和一个 S 极磁铁，如果它们两个恰好处于同一行或同一列中，那 N 极磁铁会向靠近 S 极磁铁的方向前进一格。当然，如果它们两个处于同一个格子，什么也不会发生。注意 S 极磁铁的位置是永远不会变化的。

这个方格图里的每一个格子都涂成了黑色或白色。磁铁的放置必须要遵守以下规则：

1. 每行每列都必须至少有一个 S 极磁铁。
2. 对于每个黑色格子，必须有某个 N 极磁铁通过一系列的吸引操作经过它。
3. 对于每个白色格子，无论 N 极磁铁的位置怎样变化，都不能经过它。

现在我们想知道：要满足以上三条规则，至少要放几个 N 极磁铁。如果无论怎么放都不能满足规则，请输出 $-1$。

$(1\le n,m\le 1000)$

思路：注意到，一行或一列上，如果有连续两段或两段以上的黑色块，那么一定无解。这样的话，每一个连通块一定是凸集，而且可以视作它的最小包围矩阵。我们移动这些矩阵挤到一起，那么有若干个空行或空列，设为 $rw,lc$ 。

如果这两个数一个为 $0$ 一个非 $0$ ，一定无解，因为这样一定没法放 $S$ 。否则容易构造方案使得这些空行或空列放置了 $S$ 。

AC代码：https://codeforces.com/contest/1344/submission/181194214