前言

主要用于解决显卡内存不足的问题。
梯度累积可以使用单卡实现增大batchsize的效果

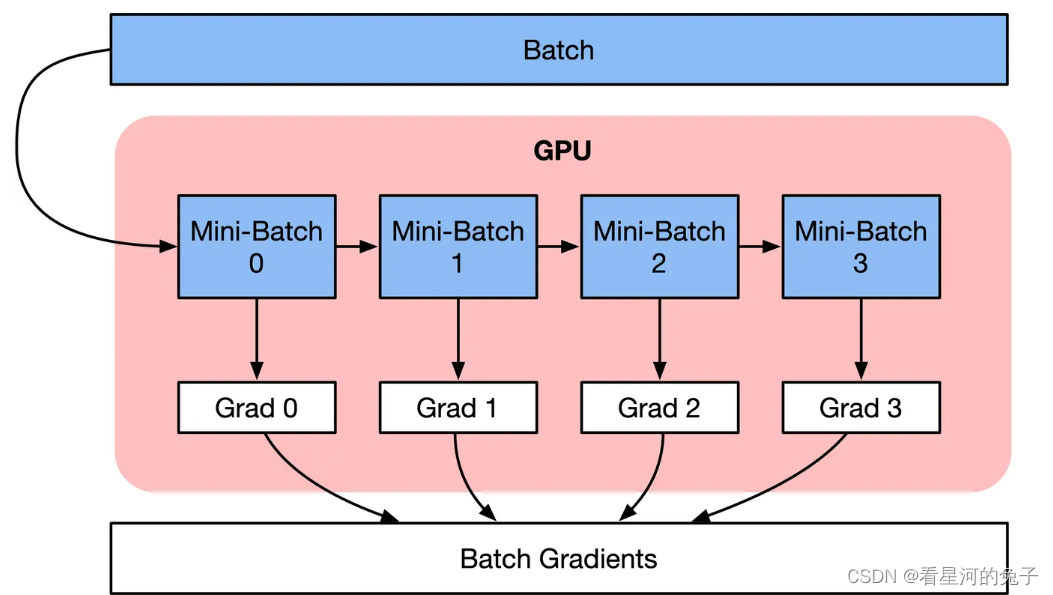
梯度累积原理

按顺序执行Mini-Batch，同时对梯度进行累积，累积的结果在最后一个Mini-Batch计算后求平均更新模型变量。
$$accumulated=\sum _{i=0}^{N}gra{d}_i$$

梯度累积是一种训练神经网络的数据Sample样本按Batch拆分为几个小Batch的方式，然后按顺序计算。
在不更新模型变量的时候，实际上是把原来的数据Batch分成几个小的Mini-Batch，每个step中使用的样本实际上是更小的数据集。
在N个step内不更新变量，使所有Mini-Batch使用相同的模型变量来计算梯度，以确保计算出来得到相同的梯度和权重信息，算法上等价于使用原来没有切分的Batch size大小一样。即：
$${\theta }_i={\theta }_{i-1}-lr\ast \sum _{i=0}^{N}gra{d}_i$$

代码实现

不加梯度累加的代码

for i, (images, labels) in enumerate(train_data):
    # 1. forwared 前向计算
    outputs = model(images)
    loss = criterion(outputs, labels)

    # 2. backward 反向传播计算梯度
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

加了梯度累加的代码

# 梯度累加参数
accumulation_steps = 4


for i, (images, labels) in enumerate(train_data):
    # 1. forwared 前向计算
    outputs = model(imgaes)
    loss = criterion(outputs, labels)

    # 2.1 loss regularization loss正则化
    loss += loss / accumulation_steps

    # 2.2 backward propagation 反向传播计算梯度
    loss.backward()

    # 3. update parameters of net
    if ((i+1) % accumulation)==0:
        # optimizer the net
        optimizer.step()
        optimizer.zero_grad() # reset grdient

代码中设置accumulation_steps = 4，意思就是变相扩大batch_size四倍。因为代码中每隔4次迭代才清空梯度，更新参数。
loss = loss/accumulation_steps，梯度累加了四次，那就要取平均除以4。同时，因为累计了4个batch，那学习率也应该扩大4倍，让更新的步子跨大点。
参考博客：1、pytorch骚操作之梯度累加，变相增大batch size
2、如何通透理解梯度累加