题目:有n阶楼梯,一次只能爬一层或者两层,请问有多少种方法?

这类题目其实都可以用斐波那契数列来解决,比如:

一阶楼梯只有一种方法

二阶楼梯有(1+1,2)两种方法

三阶楼梯有(1+1+1,1+2,2+1)三种方法

四阶楼梯有(1+1+1+1,1+2+1,1+1+2,2+2,2+1+1)五种方式

五阶楼梯有(1+1+1+1+1,1+1+1+2,1+2+2,1+2+1+1,1+1+2+1,2+1+1+1,2+2+1,2+1+2)八种方法,可以看出n阶楼梯是由(n-1) + (n-2)构成的,基数1阶为1,2阶为2.

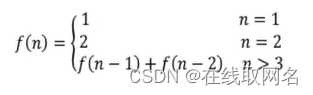
以下是代码的实现方式:

    //斐波那契数列 迭代方式实现,时间复杂度低
    private static int calculate(int n) {
        if (n==1 || n==2) {
            return n;
        }
        int first = 1, second = 2, sum = 0;
        for (int i = 3; i <= n; i++) {
            sum = first + second;
            first = second;
            second = sum;
        }
        return sum;
    }

    //递归方式  时间复杂度高(n*2)
    private static int calculate1(int n) {
        if (n==1 || n==2) {
            return n;
        }
        return calculate1(n - 1) + calculate1(n - 2);
    }

斐波那契数列结果为:89
斐波那契数列结果为:89