1.setjmp/longjmp
setjmp 和 longjmp 是C语言中用于实现基本的协程的底层函数。它们允许在一个函数的执行过程中保存当前的执行状态(包括寄存器和栈信息),然后在之后的某个时间点恢复到这个状态,从而实现函数的非局部跳转。
这两个函数通常用于实现基于栈的协程,但它们相对较底层,因此需要小心使用,以避免引入潜在的错误。
- setjmp 函数用于保存当前执行状态,并将其存储在一个 jmp_buf 结构中。jmp_buf 可以看作是一个保存了程序执行状态的数据结构。
- longjmp 函数用于从一个 jmp_buf 中恢复保存的执行状态,将程序跳转到之前保存的状态。这通常用于协程的切换,允许程序在不同的执行状态之间切换,实现协程的挂起和恢复。
以下是一个简单示例,演示了如何使用 setjmp 和 longjmp实现一个简单的协程:
#include <stdio.h>
#include <setjmp.h>
#include <unistd.h>
jmp_buf buf;
void coroutine() {
printf("Coroutine started\n");
// 模拟协程挂起
if (setjmp(buf) == 0) {
longjmp(buf, 1); // 恢复到之前保存的状态 直接跳转
printf("Will Not Print\n");//
}
printf("Coroutine resumed\n");
}
int main() {
printf("Main started\n");
coroutine();
printf("Main resumed\n");
return 0;
}
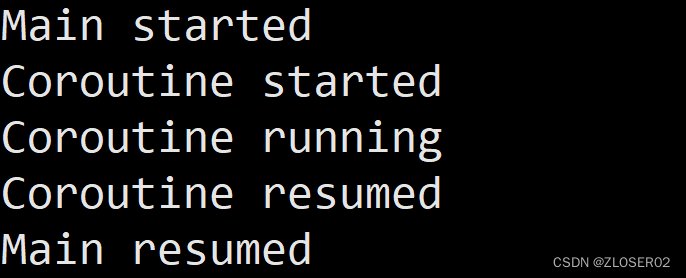
上述示例中,setjmp`保存了协程函数的执行状态,然后在 longjmp 处恢复到之前保存的状态。这就实现了一个简单的协程。但请注意,`setjmp` 和 `longjmp` 是相对底层的函数,通常不建议在实际应用中直接使用它们,因为容易引入错误。更高级的编程语言和库通常提供更安全和易用的协程实现方式。
2.ucontext
ucontext 是一个用于支持用户级线程和协程的C库,它提供了一种在用户空间中进行上下文切换的机制。ucontext 库包含了以下两个主要函数:
1. getcontext:用于获取当前执行上下文的信息,并将其保存在一个 ucontext_t 结构体中。
2. setcontext:用于将执行上下文切换到一个新的上下文,以实现线程或协程的切换。
这两个函数的使用允许在用户级别(不涉及操作系统的线程或进程切换)进行上下文切换,从而实现了协程和用户级线程。这在某些情况下可以提供更高的性能和更灵活的控制。
以下是一个简单的示例,演示了如何使用 ucontext 实现一个简单的协程:
#include<stdio.h>
#include<stdlib.h>
#include<ucontext.h>
ucontext_t ctx1,ctx2;
ucontext_t main_ctx;//main
int count=0;
void fun1(){
while(count++<20){
printf("1");
swapcontext(&ctx1,&ctx2);//协程1--->协程2
printf("2");
}
}
void fun2(){
while(count++<20){
printf("3");
swapcontext(&ctx2,&ctx1);//协程2--->协程1
printf("4");
}
}
//result: 132143214321432143214321432143214321432
int main(){
//初始化栈空间
char stack1[2048]={0};
char stack2[2048]={0};
getcontext(&ctx1);
ctx1.uc_stack.ss_sp=stack1;
ctx1.uc_stack.ss_size=sizeof(stack1);
ctx1.uc_link=&main_ctx;
makecontext(&ctx1,fun1,0);
getcontext(&ctx2);
ctx2.uc_stack.ss_sp=stack1;
ctx2.uc_stack.ss_size=sizeof(stack2);
ctx2.uc_link=&main_ctx;
makecontext(&ctx2,fun2,0);
printf("swapcontext\n");
swapcontext(&main_ctx,&ctx1);//从main--->协程1
printf("\n");
return 0;
}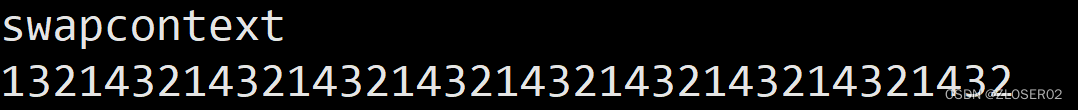
在上述示例中,我们使用 ucontext 创建了两个协程,并在 swapcontext 函数的帮助下进行了上下文切换。makecontext 函数用于指定协程的入口点函数。
请注意,ucontext 是一个相对底层的API,通常在实际应用中建议使用更高级的库或语言特性来实现协程,因为这样更容易管理和避免错误。
3.sam code (汇编实现)
(这里以X86-64寄存器为主介绍)
X86-64有16个64位寄存器,分别是:%rax,%rbx,%rcx,%rdx,%esi,%edi,%rbp,%rsp,%r8,%r9,%r10,%r11,%r12,%r13,%r14,%r15。其中:%rax 作为函数返回值使用。%rsp 栈指针寄存器,指向栈顶%rdi,%rsi,%rdx,%rcx,%r8,%r9 用作函数参数,依次对应第1参数,第2参数...(函数参数个数尽量不超过6个的原因)%rbx,%rbp,%r12,%r13,%14,%15 用作数据存储,遵循被调用者使用规则,简单说就是随便用,调用子函数之前要备份它,以防他被修改%r10,%r11 用作数据存储,遵循调用者使用规则,简单说就是使用之前要先保存原值
部分汇编代码展示:
int _switch(nty_cpu_ctx *new_ctx, nty_cpu_ctx *cur_ctx);
// %rdi %rsi
//将当前寄存器中的数据保存到cur_ctx中
//再将new_ctx的数据保存到寄存器中 从而实现程序切换
__asm__ (
" .text \n"
" .p2align 4,,15 \n"
".globl _switch \n"
".globl __switch \n"
"_switch: \n"
"__switch: \n"
" movq %rsp, 0(%rsi) # save stack_pointer \n"
" movq %rbp, 8(%rsi) # save frame_pointer \n"
" movq (%rsp), %rax # save insn_pointer \n"
" movq %rax, 16(%rsi) \n"
" movq %rbx, 24(%rsi) # save rbx,r12-r15 \n"
" movq %r12, 32(%rsi) \n"
" movq %r13, 40(%rsi) \n"
" movq %r14, 48(%rsi) \n"
" movq %r15, 56(%rsi) \n"
" movq 56(%rdi), %r15 \n"
" movq 48(%rdi), %r14 \n"
" movq 40(%rdi), %r13 # restore rbx,r12-r15 \n"
" movq 32(%rdi), %r12 \n"
" movq 24(%rdi), %rbx \n"
" movq 8(%rdi), %rbp # restore frame_pointer \n"
" movq 0(%rdi), %rsp # restore stack_pointer \n"
" movq 16(%rdi), %rax # restore insn_pointer \n"
" movq %rax, (%rsp) \n"
" ret \n"
);这只是一个非常简单的示例,实际的协程实现会更复杂,需要考虑更多的寄存器状态、错误处理、函数调用和返回等。此外,具体的汇编代码会因不同的硬件架构而异。
汇编实现切换的特点:
1.性能较高
2.容易理解
3.容易实现
a.有门槛
b.不同体系结构,汇编代码不同
c.跨平台较弱