目录
语法
说明
示例
向量模
向量的 1-范数
两个点之间的欧几里德距离
矩阵的 2-范数
N 维数组的 Frobenius 范数
常规向量范数
norm函数的功能是计算向量范数和矩阵范数。
语法
n = norm(v)
n = norm(v,p)
n = norm(X)
n = norm(X,p)
n = norm(X,"fro")说明
n = norm(v) 返回向量 v 的欧几里德范数。此范数也称为 2-范数、向量模或欧几里德长度。
n = norm(v,p) 返回广义向量 p 范数。
n = norm(X) 返回矩阵 X 的 2-范数或最大奇异值,该值近似于 max(svd(X))。
n = norm(X,p) 返回矩阵 X 的 p-范数,其中 p 为 1、2 或 Inf:
-
如果 p = 1,则 n 是矩阵的最大绝对列之和。
-
如果 p = 2,则 n 近似于 max(svd(X))。此值等效于 norm(X)。
-
如果 p = Inf,则 n 是矩阵的最大绝对行之和。
n= norm(X,"fro") 返回矩阵或数组 X 的 Frobenius 范数。
示例
向量模
创建一个向量并计算模。
v = [1 -2 3];
n = norm(v)
n = 3.7417向量的 1-范数
计算向量的 1-范数,该范数为元素模的总和。
v = [-2 3 -1];
n = norm(v,1)
n = 6两个点之间的欧几里德距离
计算两个点之间的距离作为向量元素之差的范数。创建两个向量,表示欧几里德平面上两个点的 (x,y) 坐标。
a = [0 3];
b = [-2 1];使用 norm 来计算点之间的距离。
d = norm(b-a)
d = 2.8284在几何学上,点之间的距离等于从一个点延伸到另一个点的向量的模。
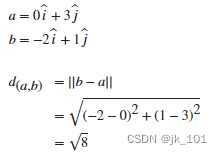
矩阵的 2-范数
计算矩阵的 2-范数,该范数为最大奇异值。
X = [2 0 1;-1 1 0;-3 3 0];
n = norm(X)
n = 4.7234N 维数组的 Frobenius 范数
计算一个 4 维数组X 的 Frobenius 范数,它等效于列向量 X(:) 的 2-范数。
X = rand(3,4,4,3);
n = norm(X,"fro")
n = 7.1247Frobenius 范数对于稀疏矩阵也很有用,因为 norm(X,2) 不支持稀疏 X。
欧几里德范数
具有N个元素的向量v的欧几里德范数(也称为向量模、欧几里德长度或 2-范数)的定义如下:
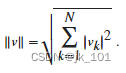
常规向量范数
具有 N 个元素的向量 v 的 p-范数的常规定义是
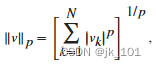
其中 p 是任何正的实数值、Inf 或 -Inf。
-
如果 p = 1,则所得的 1-范数是向量元素的绝对值之和。
-
如果 p = 2,则所得的 2-范数是向量的模或欧几里德长度。
-
如果 p = Inf,则 ‖v‖∞=maxi(∣v(i)∣)。
-
如果 p = -Inf,则 ‖v‖−∞=mini(∣v(i)∣)。
最大绝对列之和
m×n 矩阵 X (m,n >= 2) 的最大绝对列之和由
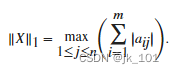
最大绝对行之和
m×n 矩阵 X (m,n >= 2) 的最大绝对行之和由
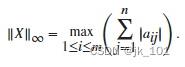
Frobenius 范数
m×n 矩阵 X (m,n >= 2) 的 Frobenius 范数由
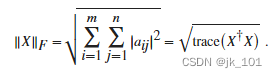
定义
此定义自然也适合扩展到二维以上的数组。例如,如果 X 是 N 维数组,大小为 m×n×p×...×q,则 Frobenius 范数为
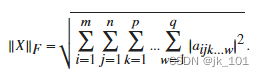
提示
-
使用 vecnorm 将矩阵或数组视为向量的集合并计算指定维度上的范数。例如,vecnorm 可以计算矩阵中每列的范数。