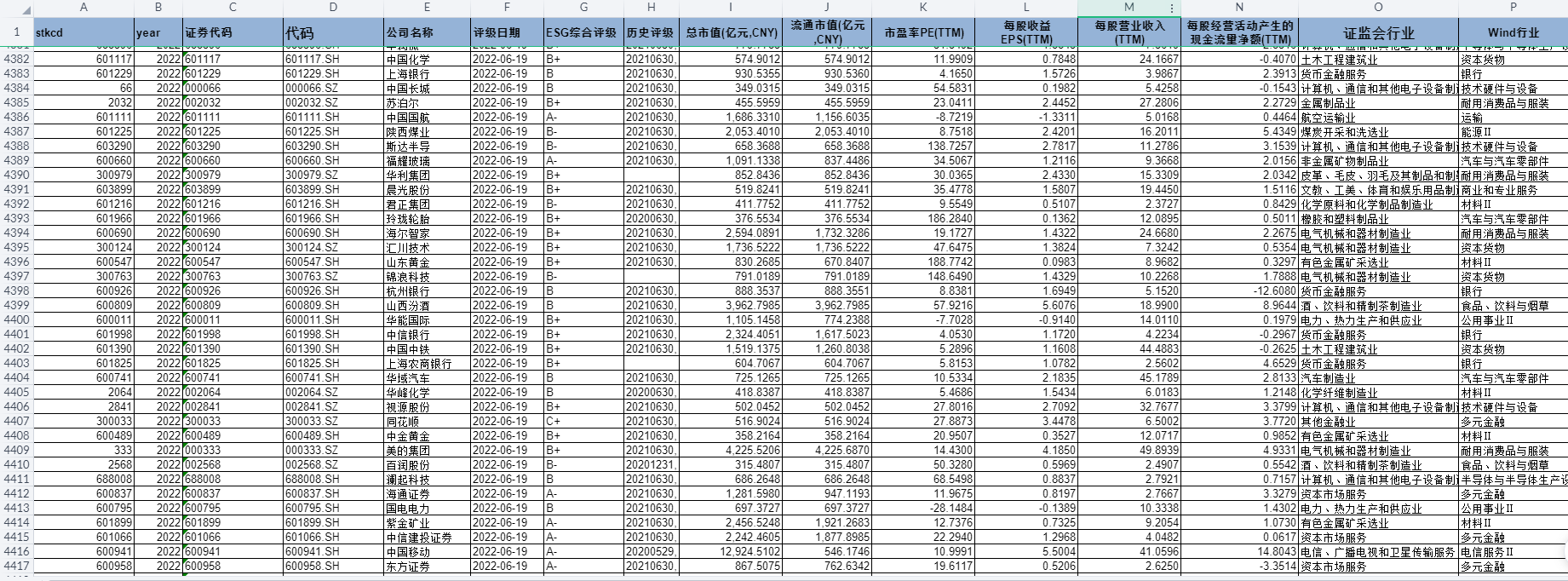
目录
一、灰色预测模型简介
二、GM(1,1)灰色模型
1、GM(1,1)模型预测方法
(1)原始数据(参考列)
(2)累加生成序列(Acumulated Generating Operator,1-AGO)
(3)生成均值数列
(4)建立灰微分方程
(5)利用最小二乘估计【2】中参数a,b
(5.1)
(5.2)构造
(6)求解方程【3】,得到预测方程
2、GM(1,1)模型的预测步骤
(1)数据的检验与处理
(2)建立模型
(3)检验预测值
(3.1)残差检验
(3.2)级差比偏差检验
(4)预测预报公式编辑【5】
一、灰色预测模型简介
灰色预测的主要特点就是模型使用的不是原始数据列,而是生成的数据序列。其核心是灰色模型(Grey Model,GM),即对原始数据作累加生成(累加或差分,都能弱化噪声)能得到近似指数规律再进行建模的方法。
优点:
- 所需数据少,一般只需要4个以上数据,能解决历史数据少,序列完整性和可靠性低的问题
- 利用微分方程来充分挖掘系统的本质,精度高
- 能将无规律的原始数据进行生成得到规律性较强的生成序列
- 运算简便,易于检验,不考虑分布规律,不考虑变化趋势
缺点:
只适合短期预测,只适合指数增长的预测。
二、GM(1,1)灰色模型
GM(1,1),表示模型是一阶微分方程,且只含一个变量的灰色模型。
1、GM(1,1)模型预测方法
(1)原始数据(参考列)
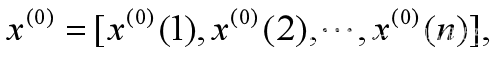
(2)累加生成序列(Acumulated Generating Operator,1-AGO)
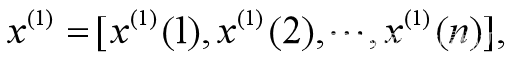
其中,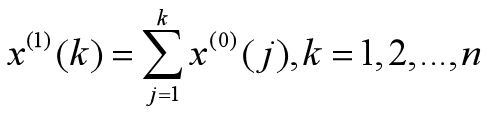 显然,数列x(1)比数列x(0)光滑,弱化噪声。
显然,数列x(1)比数列x(0)光滑,弱化噪声。
(3)生成均值数列
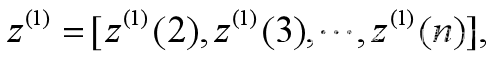 (进一步弱化噪声)
(进一步弱化噪声)
其中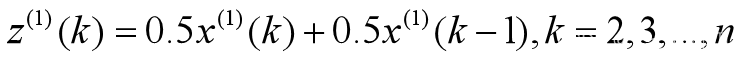
(4)建立灰微分方程
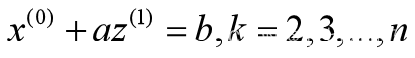 【1】
【1】
此方程白化为微分方程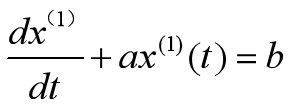 【2】
【2】
【1】的来源:x(1)是x(0)的累加,反过来,x(0)就是x(1)的差分,连续化就是导数,【1】中用z(1)而不直接用x(1),就是使数据进一步更光滑化,避免奇异值。可以利用曲线拟合来求a和b得值(就是利用最小二乘法)。用这个模型之前,最好绘制x(0),z(1)的散点图,看看大概情况。
(5)利用最小二乘估计【2】中参数a,b
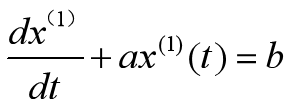 【2】
【2】
 的观测值序列为x(0)(k),k=2,3,…,n;
的观测值序列为x(0)(k),k=2,3,…,n;
【2】中x(1)(t)的观测值为z(1)(k),k=2,3,…,n;
(5.1)
把x(0),z(1)作为【2】的因变量y和自变量x,作回归拟合,得到a,b的估计值;
(5.2)构造
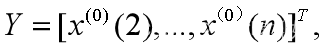
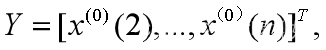
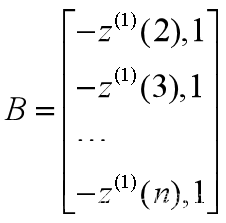
根据最小二乘法,使得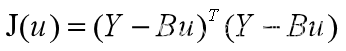 达到最小的u的估计值为
达到最小的u的估计值为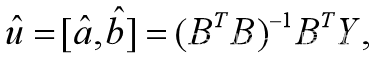 求出a,b的估计值为
求出a,b的估计值为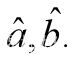 方程【2】变为
方程【2】变为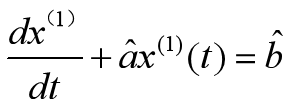
(6)求解方程【3】,得到预测方程
为了求【3】的特解,引入初值 确定特解。
确定特解。
【3】为一阶线性常系数微分方程,代入通解公式,代入定解条件,得
写成差分或者预测公式,为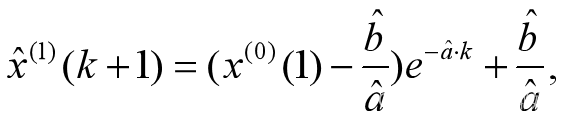 【4】k=0,1,2,…,n-1,…
【4】k=0,1,2,…,n-1,…
2、GM(1,1)模型的预测步骤
(1)数据的检验与处理
设原始数列为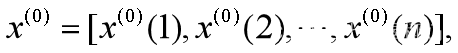 计算数列的级比
计算数列的级比
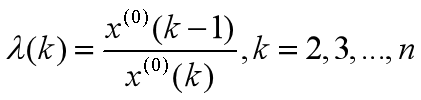
若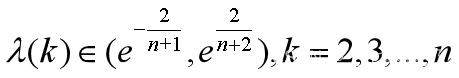 (一个包含1的区间)
(一个包含1的区间)
则认为原始数列适合作GM(1,1)灰色预测,否则需要对x(0)作平移: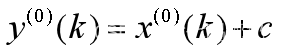 使得数列y(0)满足级比检验。
使得数列y(0)满足级比检验。
(2)建立模型
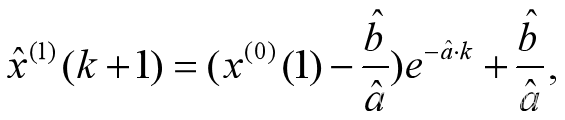 【4】
【4】
当初始数列或平移后的数列满足级比检验后,可用结论【4】进行预测,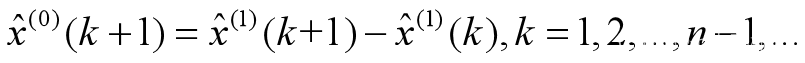
(3)检验预测值
(3.1)残差检验
计算残差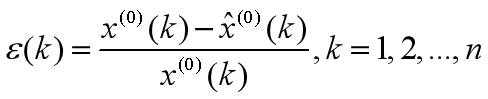
这里,
若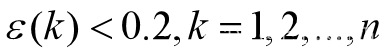 则认为预测达到一般要求;
则认为预测达到一般要求;
若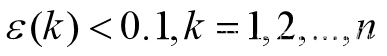 则认为预测达到较高要求;
则认为预测达到较高要求;
(3.2)级差比偏差检验
首先用原始数据x(0)(k),x(0)(k-1)计算级比λ(k),再用发展系数a求出相应的级比偏差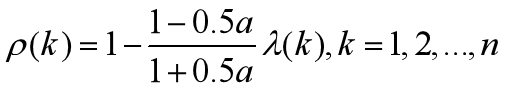
若ρ(k)<0.2,认为预测达到一般要求;若ρ(k)<0.1,则认为预测达到较高要求。这里的a就是最小二乘估计的第一个参数,称为发展系数
(4)预测预报公式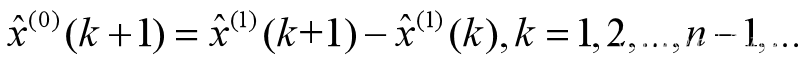 【5】
【5】