目录
一、判断链表中是否有环
(1)题目描述
(2)题解
二、环形链表的入环节点
(1)题目描述
(2)题解
一、判断链表中是否有环
(1)题目描述
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例:

输入:head = [3,2,0,-4],pos = 1
输出:true(节点有环)
(2)题解
思路分析:我们可以使用快慢指针来分析这个问题。
1.首先定义fast、slow指向head
2.快指针fast一次走两步、慢指针slow一次走一步
3.如果链表中无环,fast最终会指向null,若链表中有环,在fast和slow都进入环中后,由于fast每次比slow多走一步,fast最终会追上slow

代码实现:
public class Solution {
public boolean hasCycle(ListNode head) {
//先判断特殊情况
//若链表中为空或链表中只有一个元素,
// 则链表中无环
// 直接返回false
if (head == null || head.next == null) {
return false;
}
//定义快指针和慢指针
ListNode fast = head;
ListNode slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;//fast一次走两步
slow = slow.next;//slow一次走一步
if (fast == slow) {//fast与slow相遇,表明链表带环
return true;
}
}
//fast指向空或指向尾节点,表明链表不带环
return false;
}
}思考:
1. while条件中,能否修改为 while(fast.next != null && fast != null) ?
不能,&&(逻辑与)操作符从左到右进行判断,当左边为false时,右边的表达式不会进行运算,直接返回false,只有当左边表达式为true时,才会运算右边的表达式,若右边表达式为true,则返回true
在while条件中,应先判断fast的指向是否为空,若fast的指向为空,则不能够通过fast.next访问下一个节点,否则会抛出NullPointerException(空指针异常)。因此,while (fast != null && fast.next != null),当fast指向null时,直接返回false,而不再执行fast.next
2. 当fast走两步,slow走一步时,fast能够追上slow,当fast走三步、四步...时能否追上slow ?
当链表无环时,fast走两步、三步...都能判断链表无环
当链表有环时,我们假设fast每次走 x ( x >= 2 )步,head到入环节点有a个节点(从head到入环节点需要走a步),环上一共有C个节点,当slow走到入环节点时,fast与slow相距N(0 <= N < C)个节点
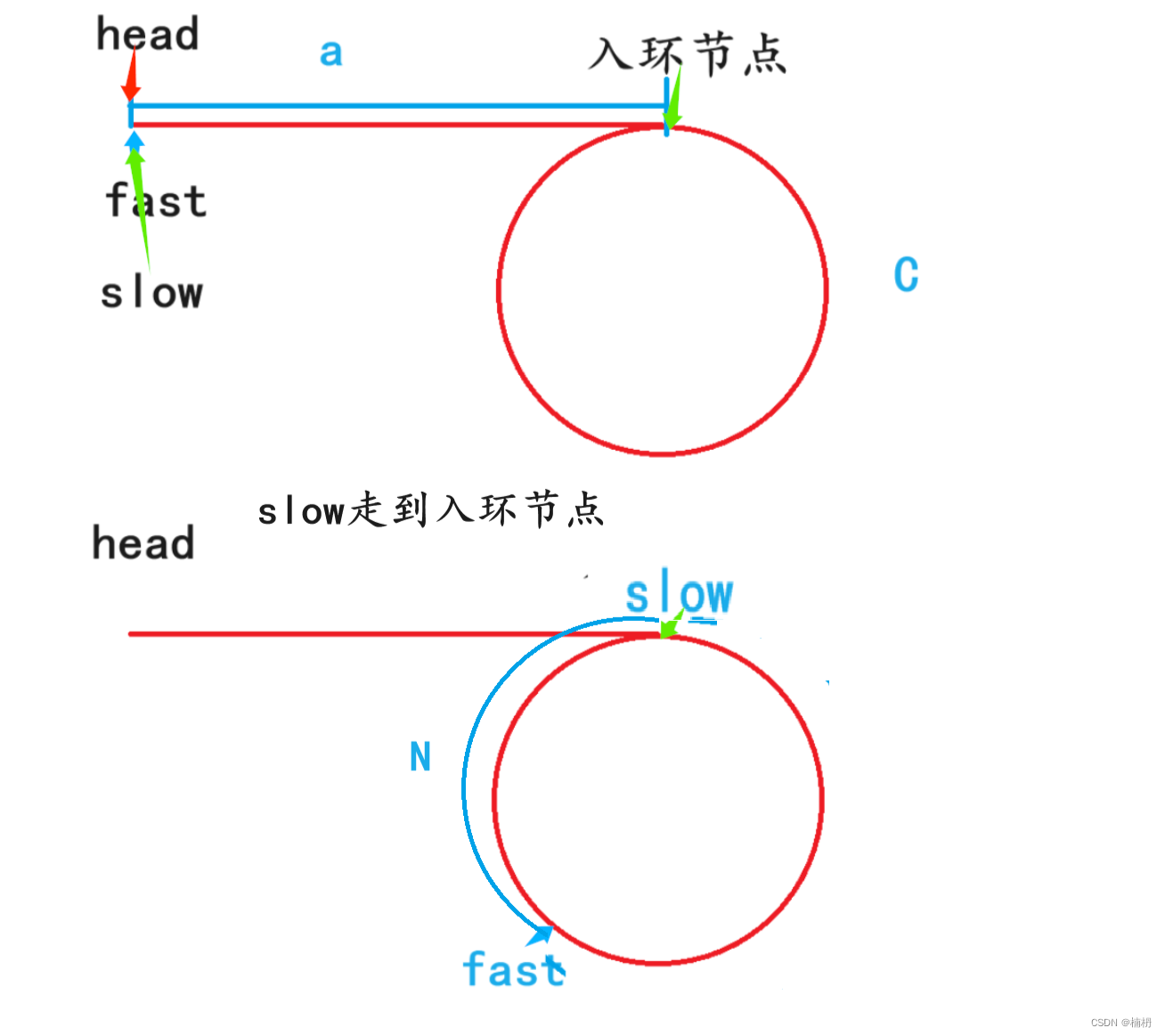
当N = 0时,fast与slow直接在入环节点相遇,因此我们考虑N > 0 且 N < C 的情况
当slow走到入环节点时,此时就是我们常说的追及问题,追及问题的公式:
追及时间(次数) = 路程差 / 速度差
我们设追及次数(即fast走多少次追上slow)为m,fast与slow之间的路程差为N,速度差为x-1,则m = N / x-1,
当x = 2时,m = N,即fast走N次就能追上slow,
当x = 3时,m = N / 2,当N为偶数时,fast 走N/2次能够追上slow;当N为奇数时,fast走了(N-1)/ 2次之后,此时fast与slow的距离为1,由于fast走三步,slow走一步,fast会反超slow 1 步
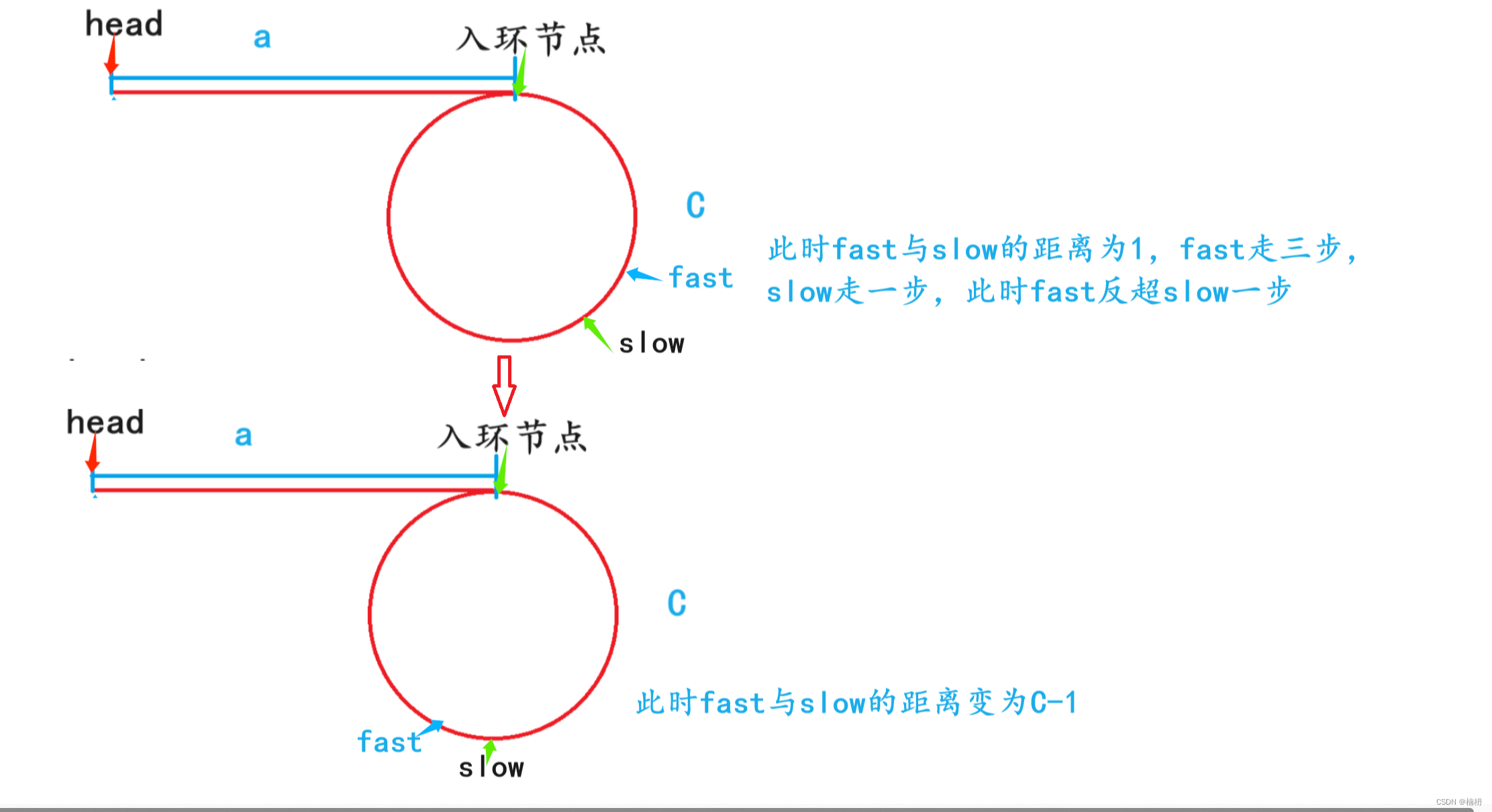
此时fast与slow的距离N变为C-1,fast重新开始追及slow,若C-1为偶数,则经过 (C-1)/2次后,fast追上slow;若C-1为奇数,在fast与slow距离为1时,fast再次反超slow,fast与slow之间的距离再次变为C-1,fast再次追及slow...如此循环,fast永远追不上slow
因此,我们可以看出,当fast一次走三步,slow一次走一步时,fast不一定能追上slow
当fast一次走四步,slow一次走一步时,分析思路与fast一次走三步一致,fast可能反超slow一步或两步,此时fast与slow的距离变为C-1 或 C-2,然后继续分情况分析
3.当fast走三步,slow走两步,或是fast走四步,slow走三步时,情况又如何呢 ?
由追及时间(次数) = 路程差 / 速度差,可以得出
当fast走三步,slow走两步 或是 fast一次走四步,slow一次走三步,fast与slow的速度差都为1,fast一定能追上slow,但
当fast一次走两步,slow一次走一步,slow走的总路程为N,即fast在一圈以内,能够追上slow
而当fast一次走三步,slow一次走两步时,slow走的总路程为2*N(2*N可能大于C),因此fast不一定在一圈之内追上slow
本题来自:
141. 环形链表 - 力扣(LeetCode)
二、环形链表的入环节点
(1)题目描述
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。不允许修改链表
示例

输入:head = [1,2],pos = 0
输出:返回索引为0的链表节点
(2)题解
思路分析:在判断链表是否有环中,我们使用快慢指针的方法来判断链表中是否有环。fast一次走两步,slow一次走一步,若链表有环,fast一定能在环中追上slow。基于这个结论,我们可以继续推出另一个结论:从头节点出发的指针会和从fast、slow相遇节点出发的指针相遇与入环节点(证明在最后)
因此,找到入环节点:
1.判断链表是否有环,无环返回null,有环找到fast与slow相遇的节点
2.让两个指针,分别从头节点、相遇点出发,当两指针汇合时,即为链表的入环节点
代码实现:
public class Solution {
public ListNode detectCycle(ListNode head) {
//链表为空,直接返回null
if(head == null){
return null;
}
ListNode fast = head;
ListNode slow = head;
while(fast.next != null && fast.next.next != null){
fast = fast.next.next;
slow = slow.next;
//找到fast与slow的相遇点
if(fast == slow){
//让fast从头节点出发,
//slow从相遇点出发,
fast = head;
while(fast != slow){
fast = fast.next;
slow = slow.next;
}//相遇节点即为入环节点
return slow;
}
}
//链表中无环,返回null
return null;
}
}为何从头节点出发的指针一定会和从fast、slow相遇节点出发的指针汇合与入环节点?
同样,当链表有环时,我们假设head到入环节点有a个节点(从head到入环节点需要走a步),环上一共有C个节点,fast与slow相遇时,与入环节点的距离为d
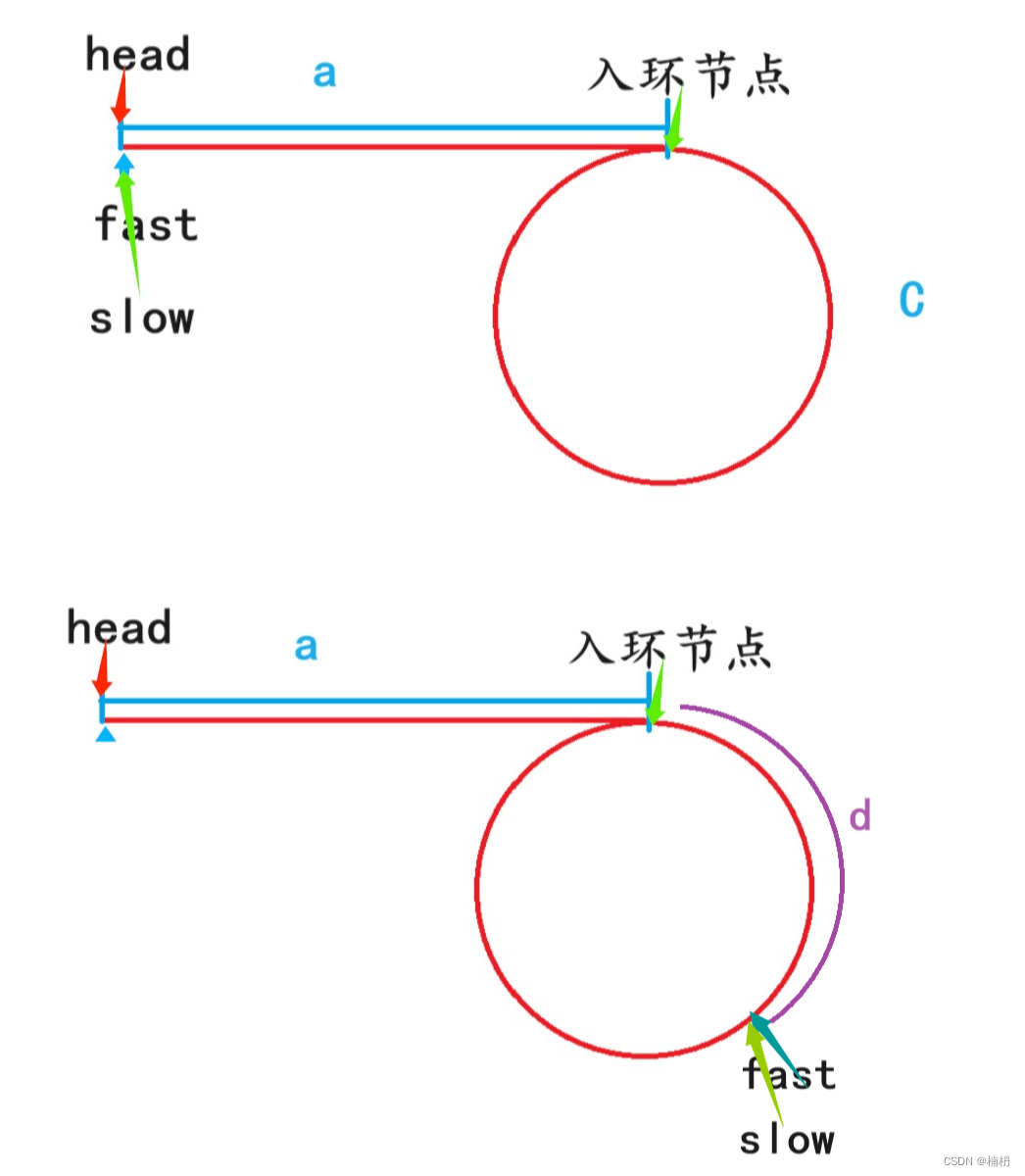
当fast与slow相遇时,
fast所走的路程为 a + n*C + d
fast所走路程为什么是a + n*C + d?
a为从头节点到入环节点的距离,当a > C时,可能slow还未进环,而fast已经在环中走了很多圈了,我们假设当fast与slow相遇时,fast在环中走了n圈,因此fast所走的路程为a + n*C + d
slow所走的路程为 a + d
由于fast的速度是slow的两倍,因此
2*(a + d)= a + n*C + d,即 a = n*C - d
将n*C化为 C*(n-1) + C,式子可化为 a =C* (n-1) + C-d,
a是从头节点到入环节点的距离,C - d 是 相遇节点距入环节点的距离,
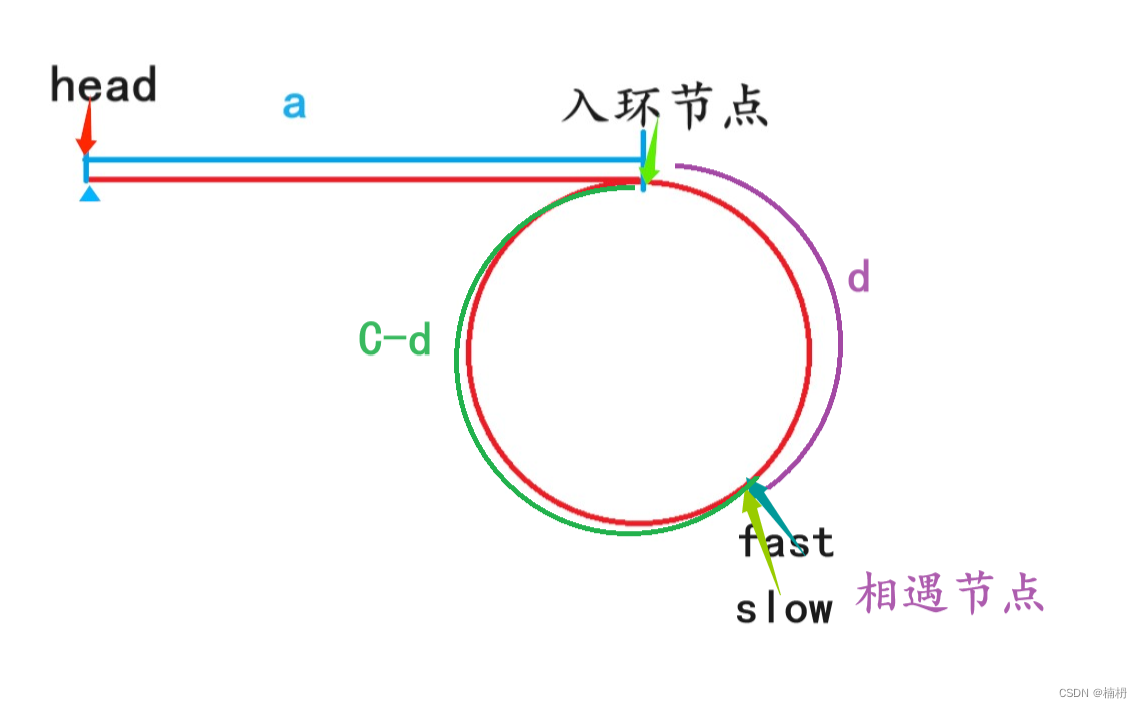
a =C* (n-1) + n-d 表明,从头节点出发的指针走 a步 等于 从相遇节点开始走的指针,走(n-1)圈后回到相遇点,再走n - d的距离,即从头节点出发的指针和从fast、slow相遇节点同时出发的指针最终会在入环节点处相遇
题目来自:
142. 环形链表 II - 力扣(LeetCode)











![[WUSTCTF2020]颜值成绩查询 布尔注入二分法](https://img-blog.csdnimg.cn/0592b587c5eb42c2b81108986f6cb789.png)
