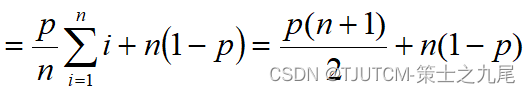重要采样的原理与实现

news2024/7/6 20:47:17

1. 引言

在雷达系统性能仿真时，由于雷达系统对虚警概率的要求，实现一定精度的仿真，所需要的Monte-Carlo实验次数将非常地高。重要采样可以在保障精度的前提下，大大降低Monte-Carlo实验次数。

网上有很多关于重要采样的原理介绍，但总体感觉过于抽象，很不好理解。有幸检索到钱键民在1984年写的一篇文章，以雷达从业者的角度介绍了重要采样。他的介绍非常的直观，下面就将该论文的内容做一简单的介绍，希望能够帮助到需要有朋友。

2. 雷达虚警概率模拟及模拟精度

雷达的虚警概率是指雷达只接收噪声时却报告存在目标的概率，即目标是虚假的概率。假设目标不存在时的雷达视频信号的概率密度函数为 $p(y)$ ，检测门限为 $T$ ，则虚警概率为

$p_{fa}=\int_T p(y)dy$

也就是说，虚警概率是噪声高于检测门限的概率。

模拟雷达系统的虚警概率时，通常是根据概率密度函数 $p(y)$ 产生一个随机数 $y$ ，将其与检测门限 $T$ 进行比较，得到一个新的随机变量

$Z_T(y)=\left\{\begin{array}{ll} 1 & y\geqslant T\\ 0 & y <T \end{array}\right.$

所以， $Z_T(y)$ 的数学期望为

$E[Z_T(y)]=p_{fa}$

又因为

$E[Z_T^2(y)]=p_{fa}$

所以， $Z_T(y)$ 的方差为

$D[Z_T(y)]=p_{fa}-p_{fa}^2\approx p_{fa}$

$Z_T(y)$ 数学期望的无偏估计为

$\hat{p}_{fa}=\frac{1}{N}\sum_{n=1}^NZ_T(y_n)$

因此，可以获得估计 $\hat{p}_{fa}$ 的均值与方差分别为

$E[\hat{p}_{fa}]=p_{fa}\\ D[\hat{p}_{fa}]=\frac{1}{N}D[Z_T(y)]=\frac{1}{N}p_{fa}$

反映一个估计量优劣的标准有两个：一个是准确度，或称可信度，由估计量的数学期望与真值之间的差值来反映；另一个是精确度，也叫可靠度，由估计量的标准差 $\sigma$ 来反映， $\sigma$ 描述了估计量在其均值附近的散布程度。

对于虚警概率估计 $\hat{p}_{fa}$ ，其是 $p_{fa}$ 的无偏估计，因此从准确度的角度，该估计量是最佳的。从精确度的角度，通常要求估计量的标准差比被估计量的标准差小一个数量级，即

$\frac{\sqrt{D[\hat{p}_{fa}]}}{\sqrt{D[Z_T(y)]}}=10^{-1}$

将上式整理可得

$N=\frac{10^2}{p_{fa}}$

显然，要使模拟精度高出 $p_{fa}$ 一个数量级，在 $p_{fa}=10^{-6}$ 时，模拟次数 $N=10^8$ 。

3. 提高模拟精度的途径

设随机变量 $X$ 的数学期望 $\mu$ 与方差 $\sigma^2$ 未知，已经获得该随机变量 $N$ 个独立样本 $X_1, X_2, \cdots, X_N$ ，则 $X$ 数学期望和方差的估计分别为

$\bar{X}=\frac{1}{N}\sum_{i=1}^NX_i\\ s^2=\overline{D[X]}=\frac{1}{N-1}\sum_{i=1}^N(X_i-\bar{X})^2$

估计量 $\bar{X}$ 的方差为

$D[\bar{X}]=\frac{s^2}{N}$

根据切比雪夫（Chebyshev）

$P[|\bar{X}-\mu|\leqslant \varepsilon]\geqslant 1-\frac{D[\bar{X}]}{\varepsilon^2}=1-\frac{s^2}{\varepsilon^2 N}$

对于给定置信度 $\alpha$ ，令

$\alpha = 1-\frac{s^2}{\varepsilon^2 N}$

则

$\varepsilon = \frac{s}{(1-\alpha)\sqrt{N}}$

因此Monte-Carlo模拟的准确度是 $O(\frac{1}{\sqrt{N}})$ ，当 $n$ 增大时，收敛速度是 $O(\frac{1}{\sqrt{N}})$ 。另外，降低方差估计 $s^2$ ，也可以提高准确度 $\varepsilon$ 。

4. 重要采样技术

假设一个随机变量 $\eta$ ，其服从经过畸变后的密度函数 $g(\eta)$ ， $g(\eta)$ 与 $p(y)$ 具有相同的定义域，从而

$p_{fa}=\int_Tp(y)dy=\int_T\frac{p(y)}{g(y)}g(y)dy$

定义随机变量

$Z_T(\eta)=\left\{\begin{matrix} 1 & \eta\geqslant T\\ 0 & \eta< T \end{matrix}\right.$

和随机变量函数

$\omega(\eta)=\frac{p(\eta)}{g(\eta)}$

习惯上称 $\omega(\eta)$ 为加权函数。利用 $Z_T(\eta)$ 和 $\omega(\eta)$ 可形成一个新的随机变量

$Z(\eta)=Z_T(\eta)\omega(\eta)$

其数学期望为

$E[Z(\eta)] = \int Z_T(\eta)\omega(\eta)g(\eta)d\eta\\ ~~~~~~~~~~~= \int_T\omega(\eta)g(\eta)d\eta\\ ~~~~~~~~~~~= \int_Tp(\eta)d\eta = p_{fa}$

所以可得到 $p_{fa}$ 的另一种形式的最佳无偏估计

$\hat{p}'_{fa}=\frac{1}{N}\sum_{i=1}^NZ(\eta)\\ ~~~~~=\frac{1}{N}\sum_{i=1}^NZ_T(\eta)\omega(\eta)\\ ~~~~~=\frac{1}{N}\sum_{i=1,\eta\geqslant T}^N\omega(\eta)$

随机变量 $Z(\eta)$ 的方差

$D[Z(\eta)]=\int [Z(\eta)]^2g(\eta)d\eta-p^2_{fa}\\ ~~~~~~~~~~~=\int [Z_T(\eta)\omega(\eta)]^2g(\eta)d\eta-p^2_{fa}\\ ~~~~~~~~~~~=\int_T\frac{p^2(\eta)}{g(\eta)}d\eta-p^2_{fa}$

重要采样技术成败的关键在于如何选取畸变密度函数 $g(\eta)$ ，使方差D[Z(\eta)]尽可能地小。

由于 $p_{fa}$ 通常是一个很小的量，畸变密度函数 $g(\eta)$ 的选取要满足：

在 $(T,\infty)$ 的范围内， $\omega(\eta)$ 的值尽可能地小，即在此区间 $g(\eta)$ 要比 $p(\eta)$ 尽可能地大
为使实验次数尽可能地少，应该尽量减少失败次数，即概率

$P[Z_T(\eta)]=P[\eta\geqslant T]=\int_T g(\eta)d\eta$

尽可能地大。

通常畸变密度函数 $g(\eta)$ 总选择与 $p(\eta)$ 的函数形式一样，只是其中的参量不同，使得 $p(\eta)/g(\eta)$ 在 $(T,\infty)$ 上接近一个常量。

重要采样的具体步骤：

选取畸变概率密度函数 $g(\eta)$ ，产生服从 $g(\eta)$ 的随机变量 $\eta$ ；
把 $\eta$ 与门限 $T$ 进行比较，得 $Z_T(\eta)$ ；
计算 $\omega(\eta)=p(\eta)/g(\eta)$ ，计算 $\hat{p}'_{fa}$

5. 重要采样示例

设随机变量 $y$ 服从Rayleigh分布，其概率密度函数为

$p(y)=\frac{y}{\sigma^2_1}\exp\{-\frac{y^2}{2\sigma^2_1}\}$

虚警概率

$p_{fa}=\int_Tp(y)dy\\ ~~~~~=\exp\{-\frac{T^2}{2\sigma_1^2}\}$

选取畸变概率密度函数

$g(y)=\frac{y}{\sigma^2_2}\exp\{-\frac{y^2}{2\sigma^2_2}\}$

从而权函数

$\omega(y)=\frac{p(y)}{g(y)}=\frac{\sigma_2^2}{\sigma_1^2}\exp\{-\frac{y^2}{2}(\frac{1}{\sigma_1^2}-\frac{1}{\sigma_2^2})\}$

产生随机变量 $\eta\sim g(\eta)$ ，与门限 $T$ 比较得 $Z_T(\eta)$ ，采用重要采样技术后 $p_{fa}$ 的估值为

$\hat{p}'_{fa}=\frac{1}{N}\sum_{i=1}^NZ_T(\eta_i)\omega(\eta_i)$

由前面讨论可知，估计是无偏的，即

$E[\hat{p}'_{fa}]=p_{fa}$

且有

$\frac{D[\hat{p}'_{fa}]}{p^2_{fa}}=\frac{1}{N}\left[\frac{\sigma_2^2}{\sigma_1^2}\frac{1}{(2-\sigma_1^2/\sigma_2^2)}\exp\{\frac{T^2}{2\sigma_2^2}\} - 1 \right ]$