目录
归并排序
快速排序
1 挖坑法编辑
2 Hoare法
快排的优化
快排的非递归方法
七大排序算法复杂度及稳定性分析
归并排序
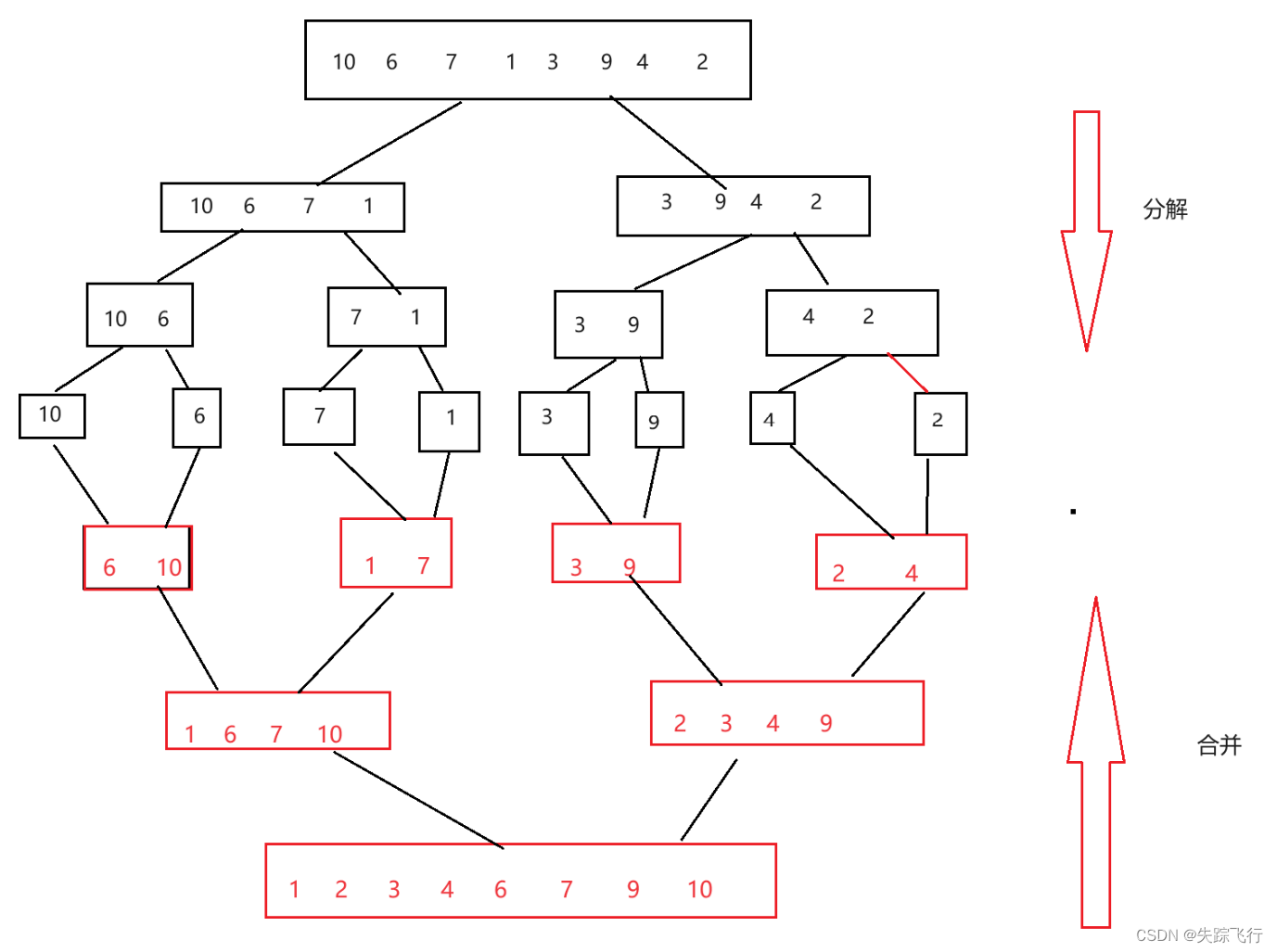
归并排序是建立在归并操作上的一种有效的排序算法,将以有序的子序列合并,得到完全有序的序列,即先使每个子序列有序,在使子序列段间有序.若将两个有序的序列合并成一个有序表,成为二路归并.
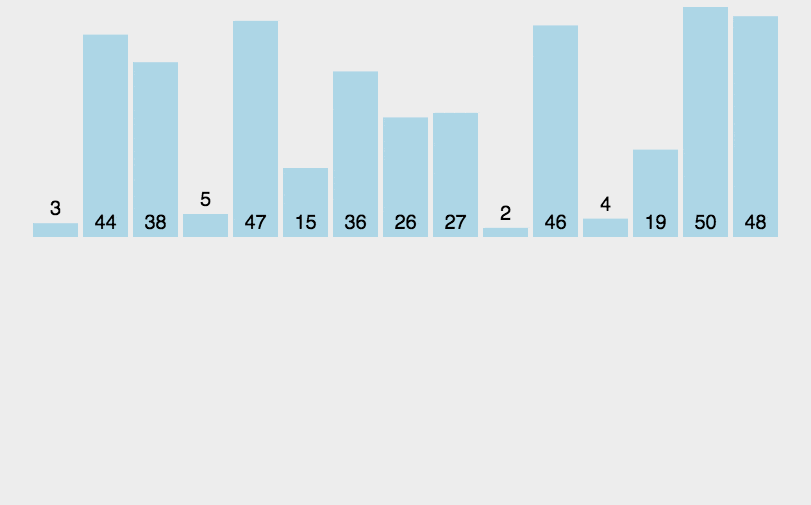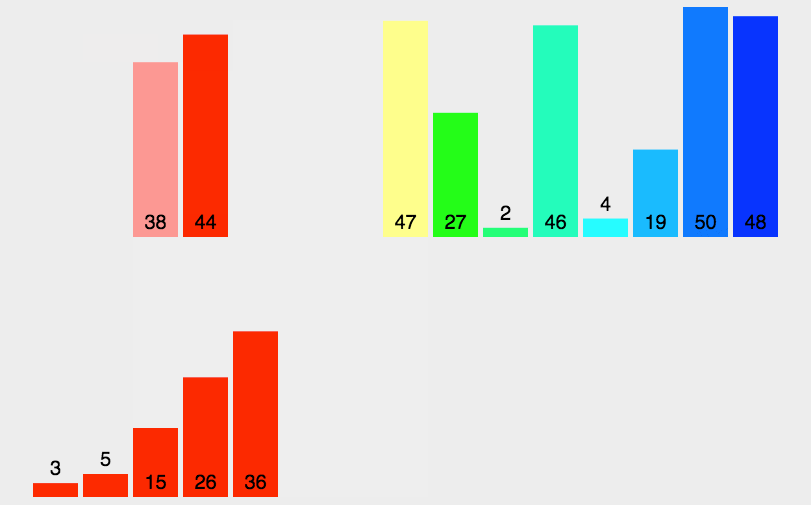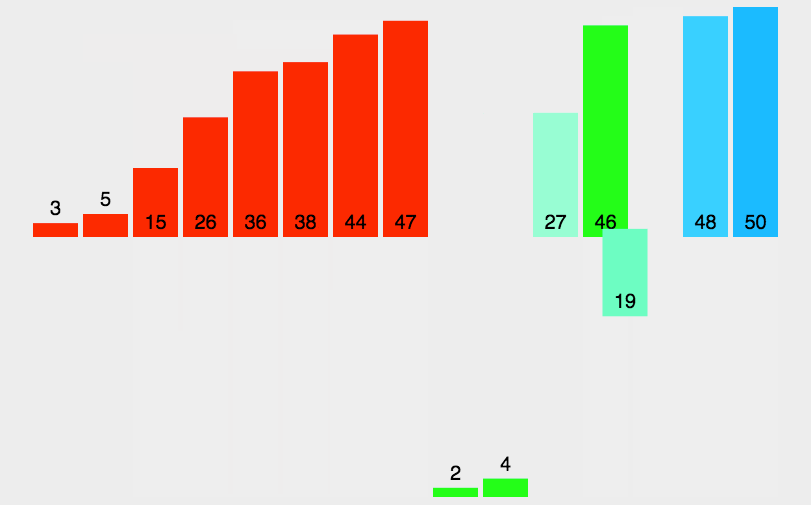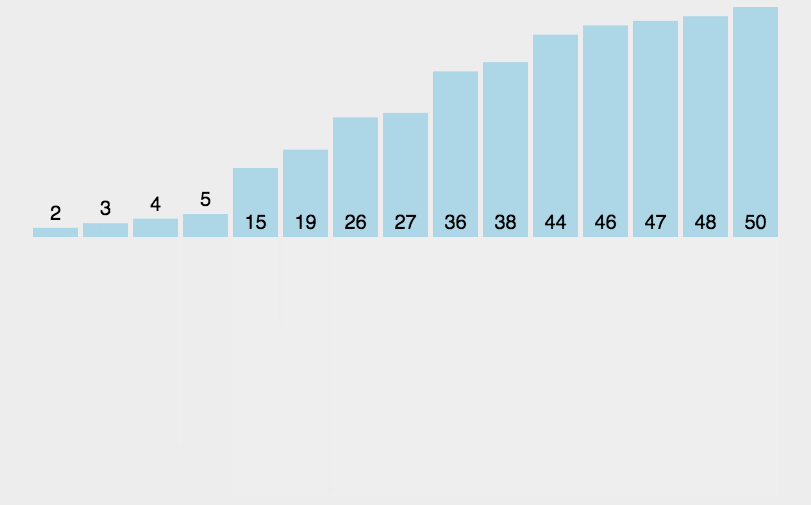
归并排序的递归写法:
1: 首先建行区间一分为二,分裂点 : mid = ( left + right ) / 2;
2: 递归的对两个子区间array[left..mid] 和 array[mid+1 ... right]进行归并排序.递归的终止条件是子区间的长度为1.
3: 将两个子区间归并为一个有序的空间.但我们归并右树的时候不是从原来数组的0下标开始,所以我们在归并的时候要加上他原来数组所在的下标 即 array[i + start] = tmp[i];
代码:
public void mergeSort(int[] array) {
sort(array,0,array.length-1)
}
private void sort(int[] array,int left,int right) {
if(left >= right) {
return;
}
int mid = (left + right) / 2;
sort(array,left,mid);
sort(array,mid+1,right);
//合并
merge(array,left,right,mid);
}
//合并
private void merge(int[] array,int start,int end,int mid) {
int s1 = start;
int s2 = mid + 1;
int[] tmp = new int[end - start + 1];
int k = 0;
while(s1 <= mid && s2 <= end) {
if(array[s1] <= array[s2]) {
tmp[k++] = array[s1++];
} else {
tmp[k++] = array[s2++];
}
}
while(s1 <= mid) {
tmp[k++] = array[s1++]
}
while(s2 <= end) {
tmp[k++] = array[s2++];
}
for (int i = 0; i < tmp.length; i++) {
array[i + start] = tmp[i];
}
}
}归并排序的非递归写法:
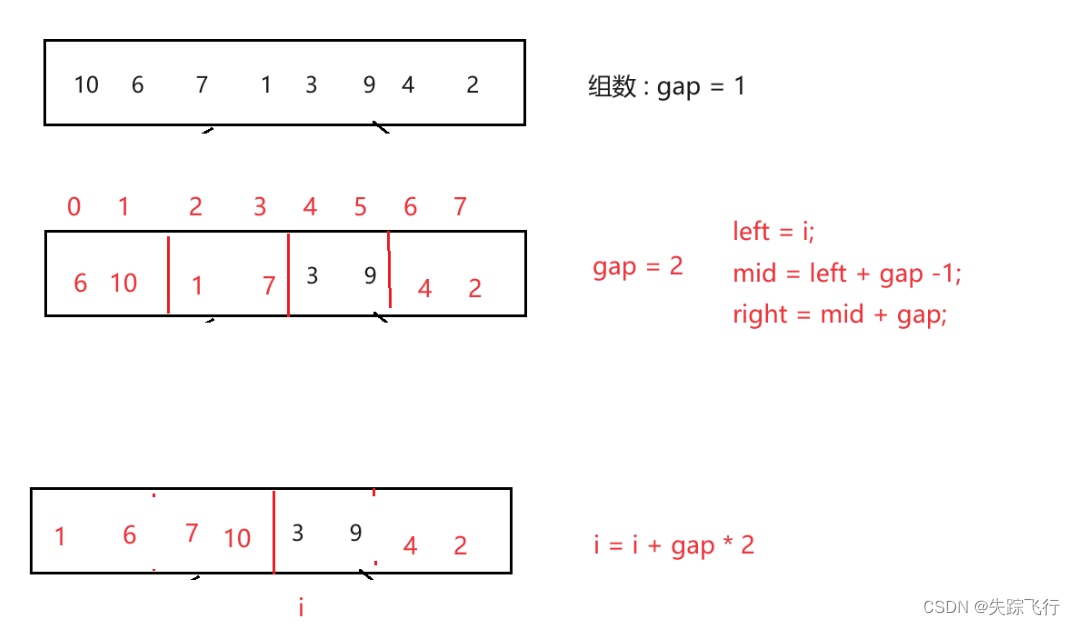
首先将一组序列的每个元素看做一个单独的序列,进行比较之后排好序,然后在每两个一组进行比较,直到组数和和序列的个数相同,序列就拍好序了
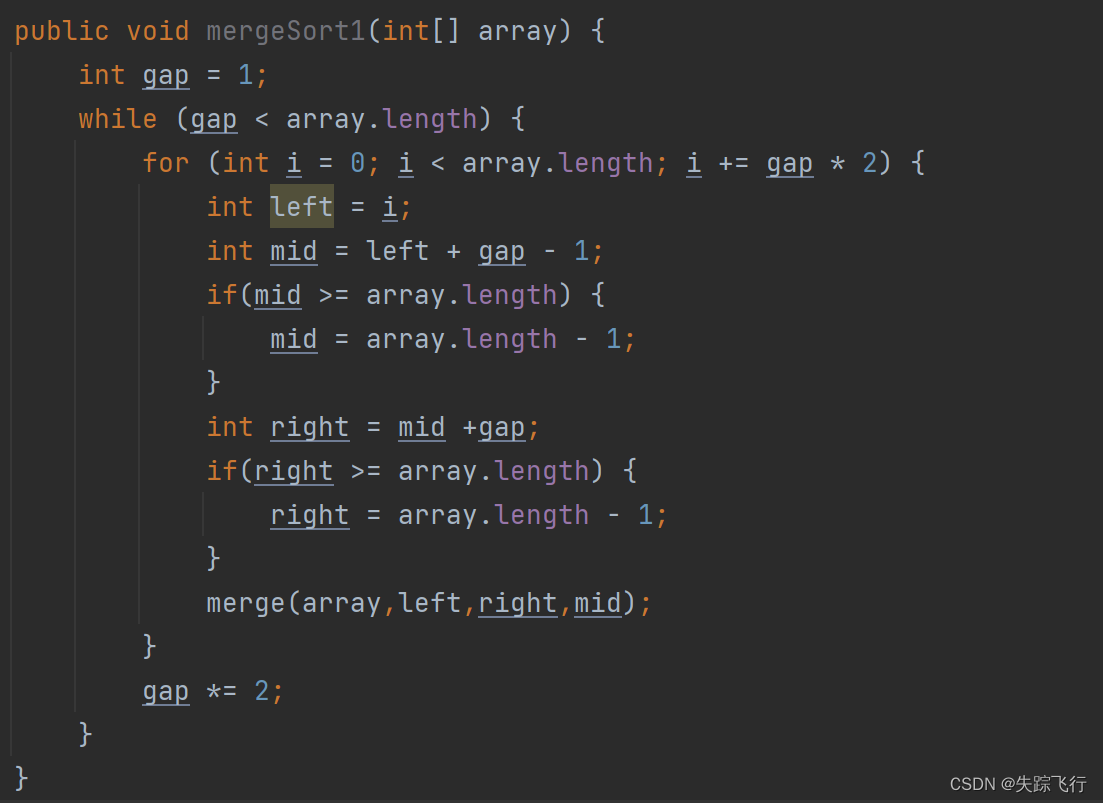
归并排序的特性总结 :
归并排序的时间复杂度是O(N* log₂N),空间复杂度是O(N),稳定性是稳定的排序
快速排序
快速排序是一种二叉树结构的交换排序方法,其基本思想是任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序结合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后按照左右子序列重复该过程,直到所有元素排列在相应位置上位置.
动图展示
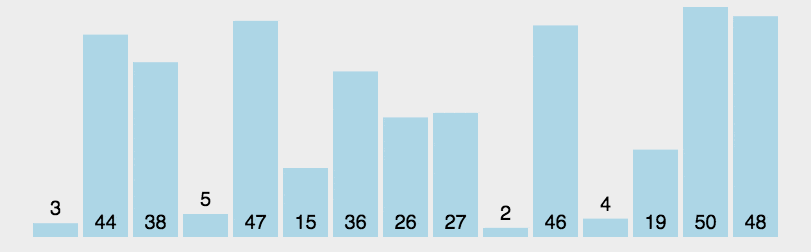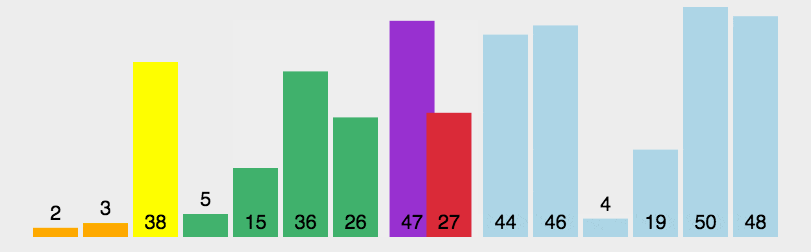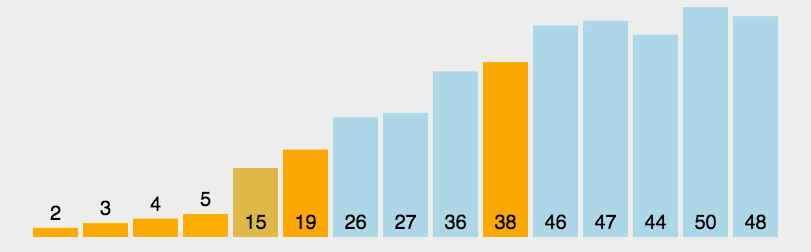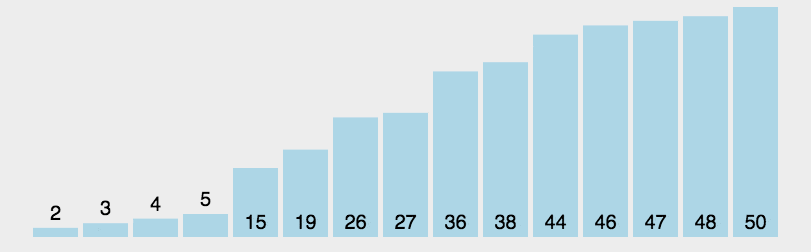
快速排序有很多方法,在这里我主要讲两种方法
1 挖坑法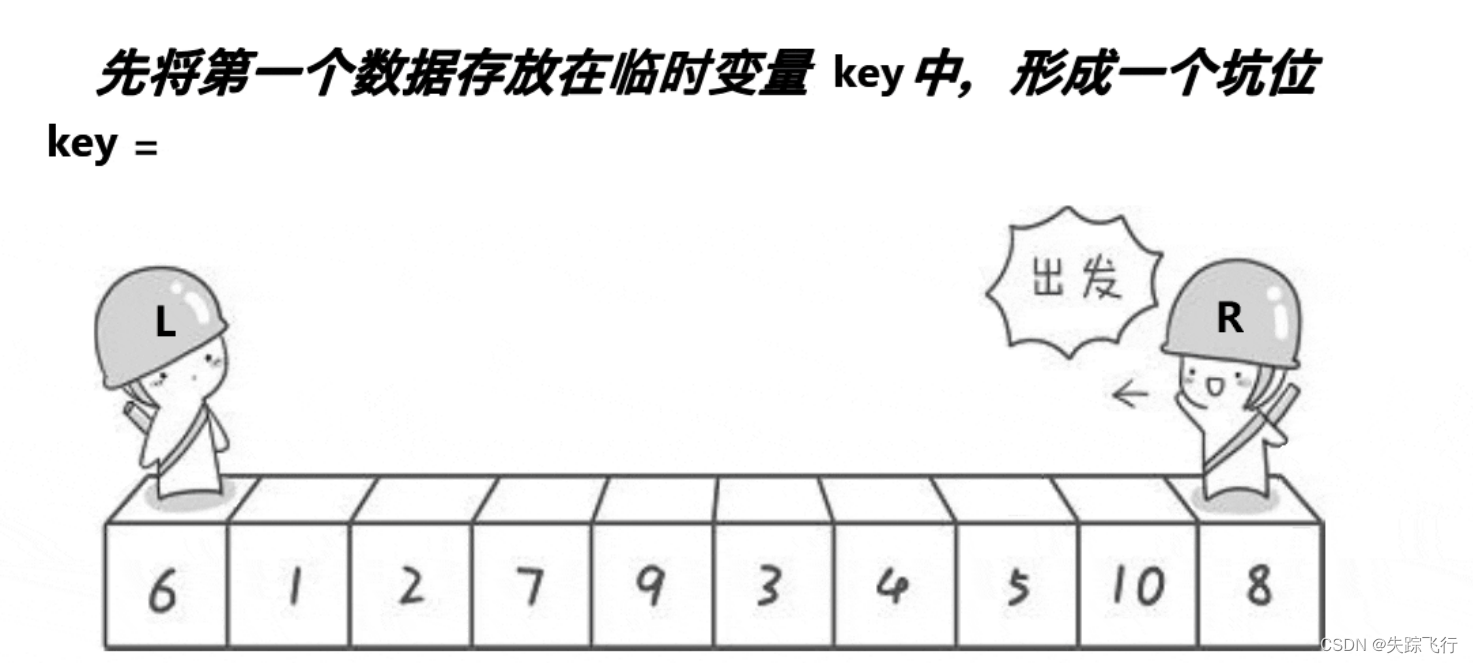
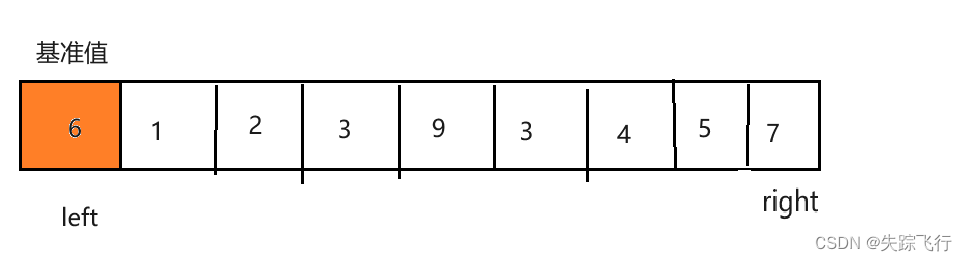
首先我们在这个排序序列中随便找一个基准值,通常为了方便,以第一个数作为基准值,然后我们从后往前找比基准值小的元素,找到后把这个元素放到基准值的位置
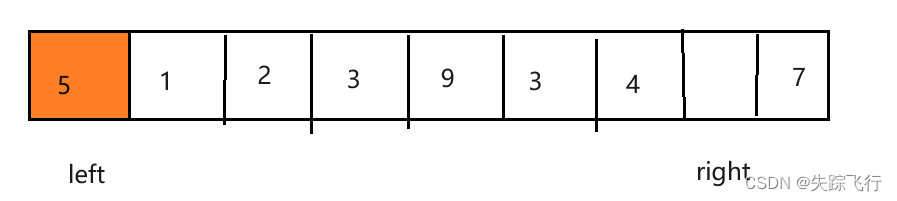
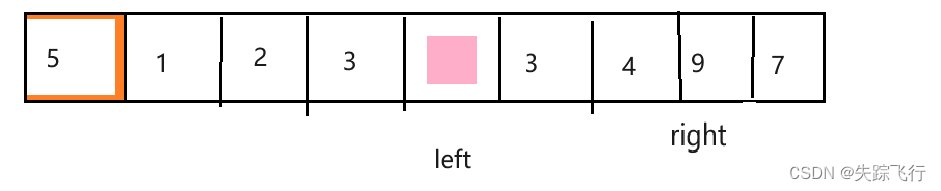
然后我们从前往后找比基准值大的元素,然后把这个元素放到坑里.会出现一个新的坑
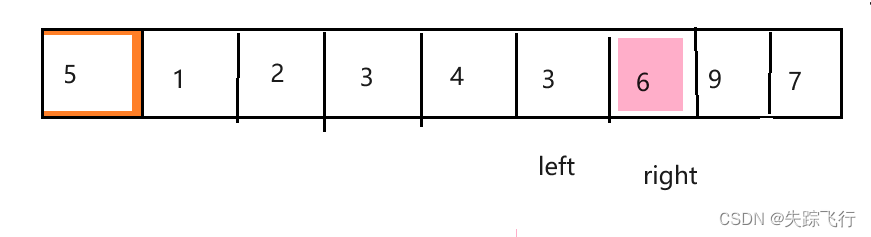
然后重复上面操作直到将left和right相遇,我们把基准值放到坑位里面.
代码展示
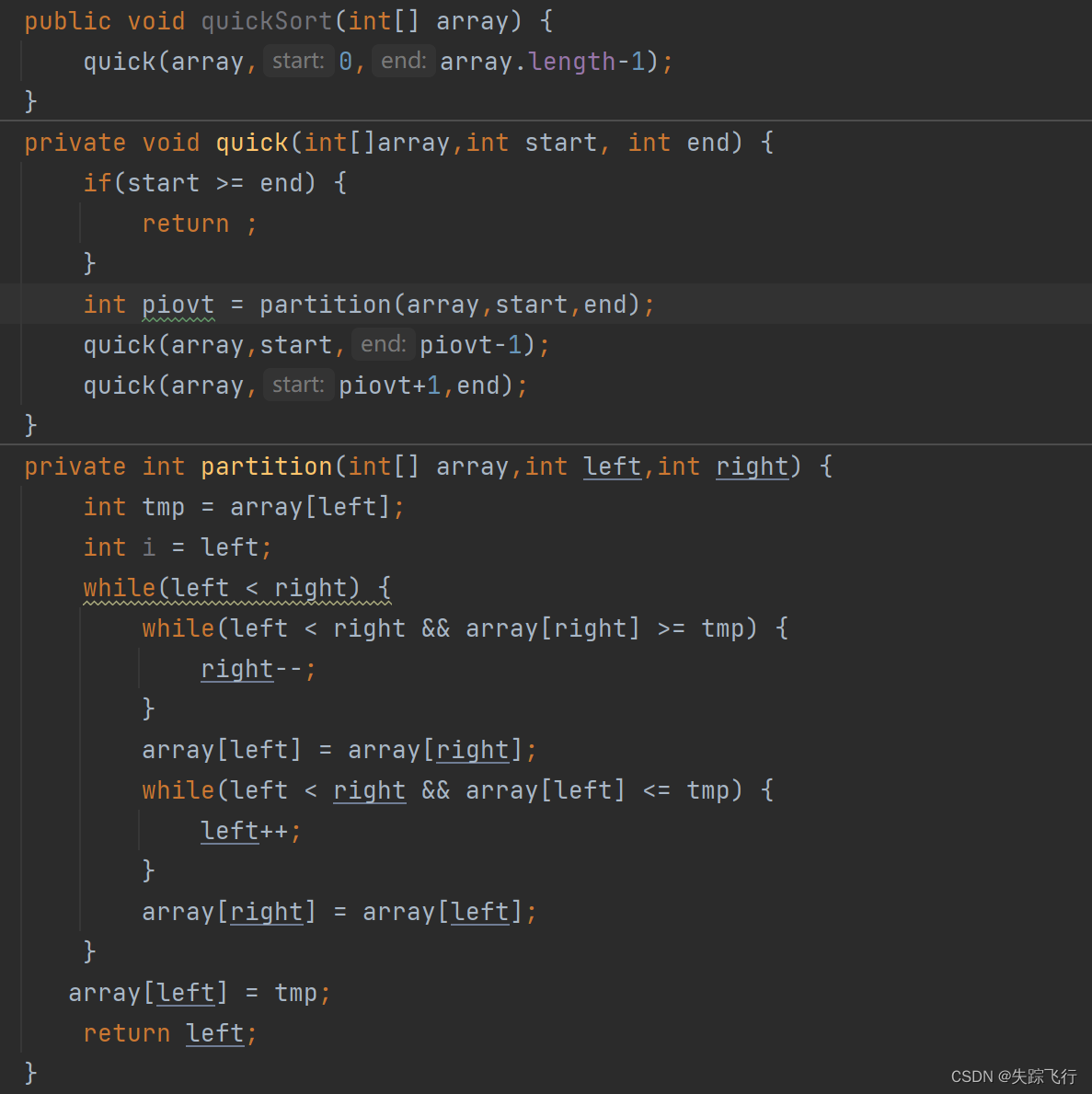
大家想想,我们在内层while循环中, <= 和 >=能换成> 和 < 吗?
答案是不可以的
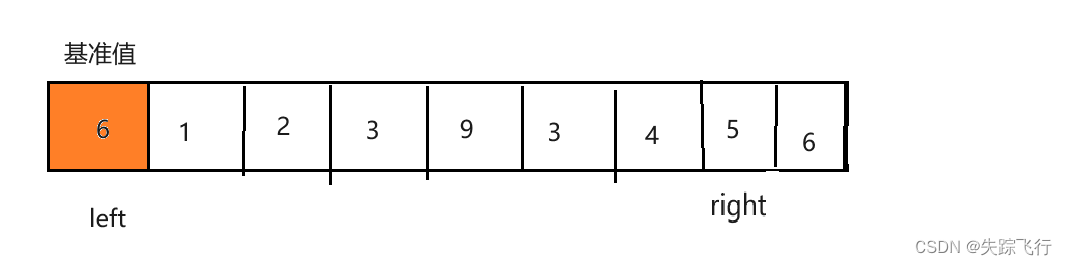
当最后一个元素和第一个元素大小相等的时候,如果取 > 和 < 的情况下,是要进行和基准值交换的,当从后往前走完后,从前往后走,又满足交换条件,这样就成了死循环.
2 Hoare法
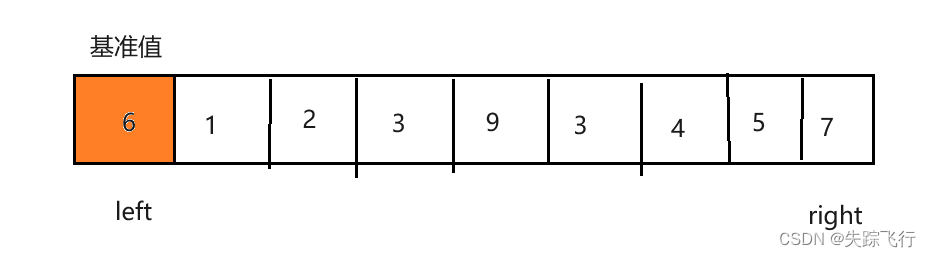
同样的方法我们先找一个基准,然后从后往前找比基准值小的,找到后从前往后找比基准值大的,找到后交换两个的位置
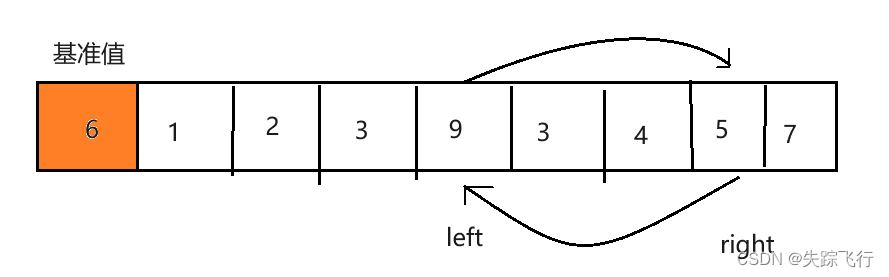然后重复上面的操作直到lleft和right相遇
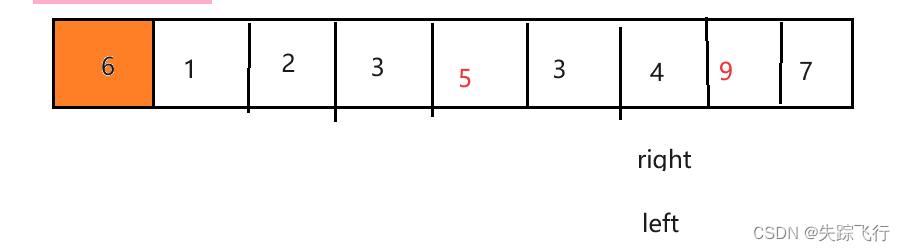
然后让array[left] 和基准值交换位置,我们发现比基准值小的都在基准值的左边,比基准值大的都在基准值的右边
根据两种方法的比较,我们会发现两种序列的顺序是不一样的,
当我们左边找基准值的时候,为什么要从右边先走呢?
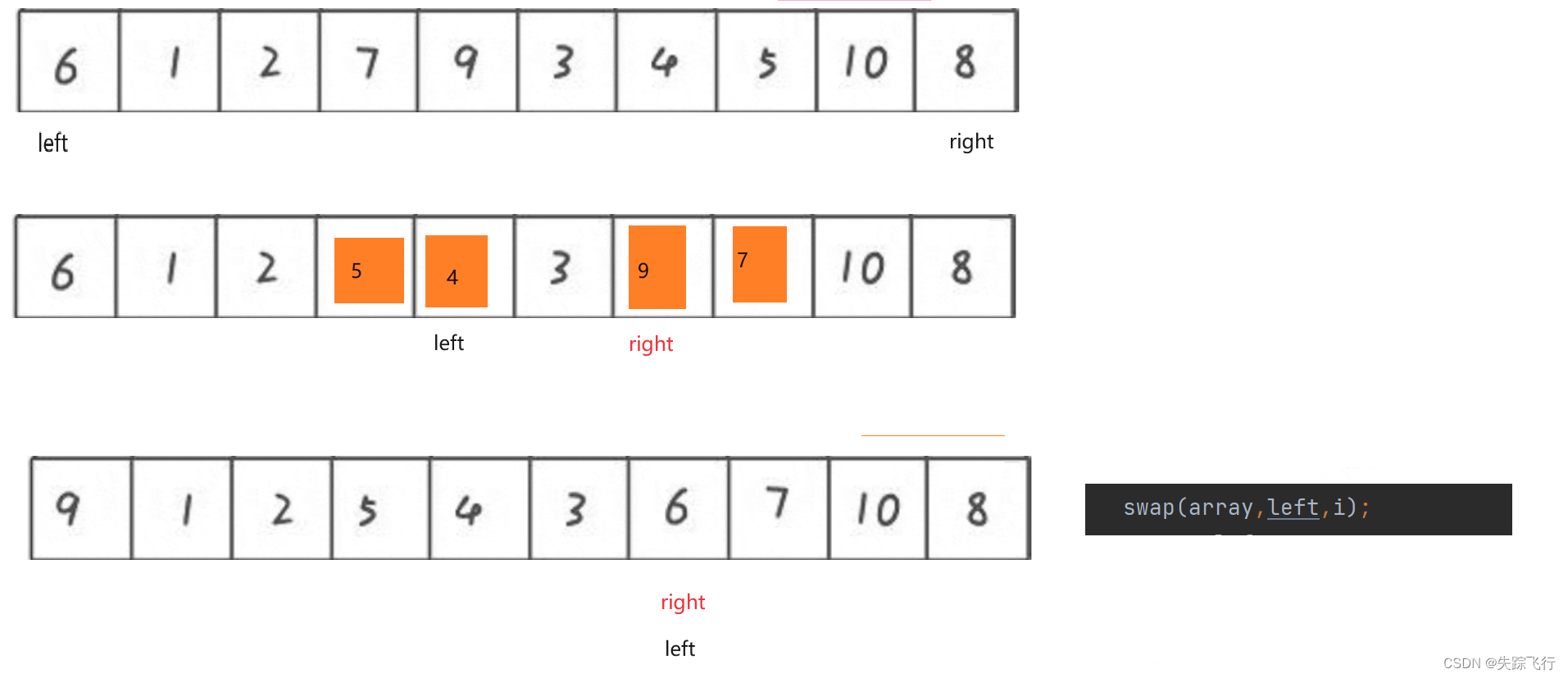
以Hoare法为例,当我们先从左边走,在走右边,交换后right位置的值一定比基准值大,当Left和right相遇的时候,将左边的值和基准值交换,较大值就排到前面去了,就不满足基准值左边的都比基准值小的性质了
快速排序的基本特性
快速排序是一种二叉树结构的交换排序方法.
时间复杂度: 最好的情况 O(N * log₂ N) ,最坏的情况给的序列本来就有序,在递归的时候只会是一棵单支树,树的高度就为N,时间复杂度为O(N ^ 2),
空间复杂度: 最好情况: O(log₂ N), 最坏情况 : O(N)
稳定性: 不稳定的
快速排序需要再系统内部用一个栈来实现递归,每层递归调用时的指针和参数均需要用栈来存放,快速排序的递归过程可以用一颗二叉树来表示,当数据量较大时,在最坏的情况时,可能会发生栈溢出异常,所以我们要对快速排序进行优化.
快排的优化
三数取中法
在一组排序序列中,我们选取三个数,分别是第一个数,中间位置的数和最后一个数,在这三个数中选取中间大的数作为基准数. 这样就不会出现单支树的情况.
如何在三个数中找中间大的数呢?
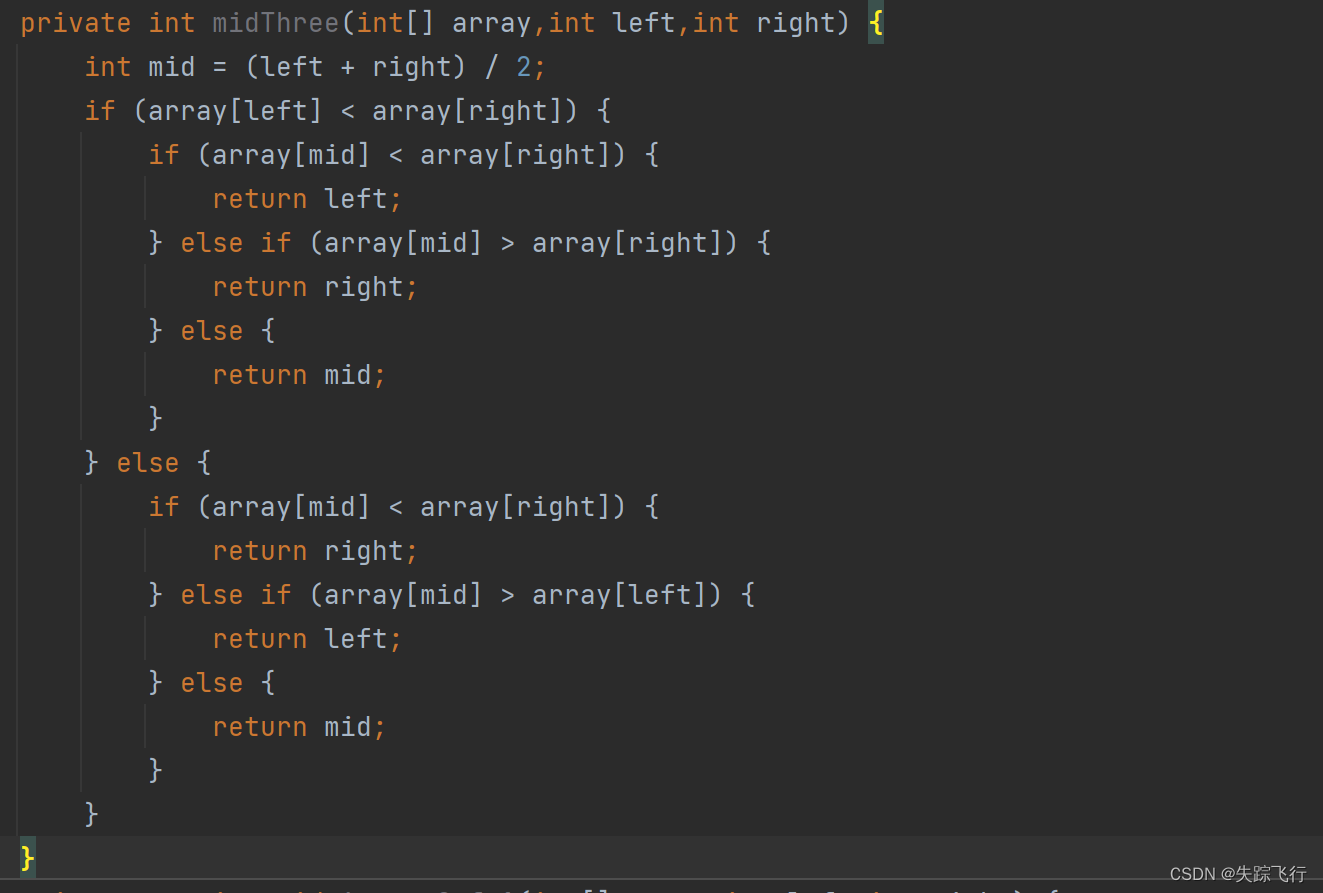
快速排序是一种二叉树结构的交换排序方法.在二叉树中,层数越多,下面的节点数就越多,也趋于有序,在后面两层可以直接使用直接插入法进行排序,减少递归的次数.
public void quickSort(int[] array) {
quick(array,0,array.length-1);
}
private void quick(int[]array,int start, int end) {
if(start >= end) {
return ;
}
if(end - start + 1 <= 14) {
//插入排序
insertSoft2(array,start,end);
return;
}
int index = midThree(array,start,end);
swap(array,index,start);
int piovt = partition(array,start,end);
quick(array,start,piovt-1);
quick(array,piovt+1,end);
}
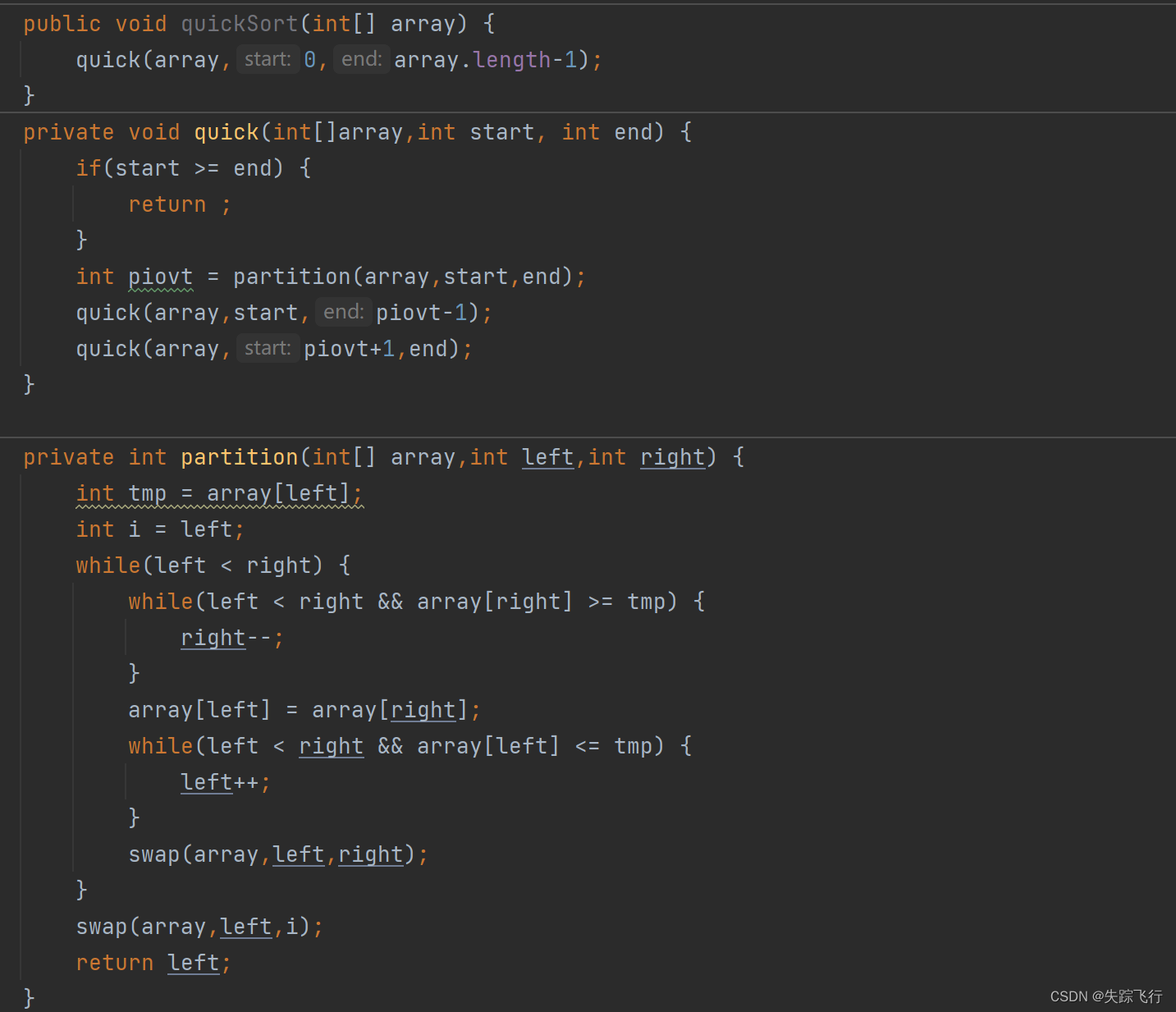
private int partition(int[] array,int left,int right) {
int tmp = array[left];
int i = left;
while(left < right) {
while(left < right && array[right] >= tmp) {
right--;
}
array[left] = array[right];
while(left < right && array[left] <= tmp) {
left++;
}
swap(array,left,right);
}
swap(array,left,i);
return left;
}
public static void insertSoft2(int[] array,int left,int right) {
for(int i = left+1; i <= right;i++) {
int tmp = array[i];
int j = i -1;
for(j =i-1; j >= left ;j--) {
if(array[j] > tmp) {
array[j+1] = array[j];
} else {
array[j+1] = tmp;
break;
}
}
array[j+1] = tmp;
}
}快排的非递归方法
在第一次找到基准值之后,我们将基准值左边和右边的下标放到栈中,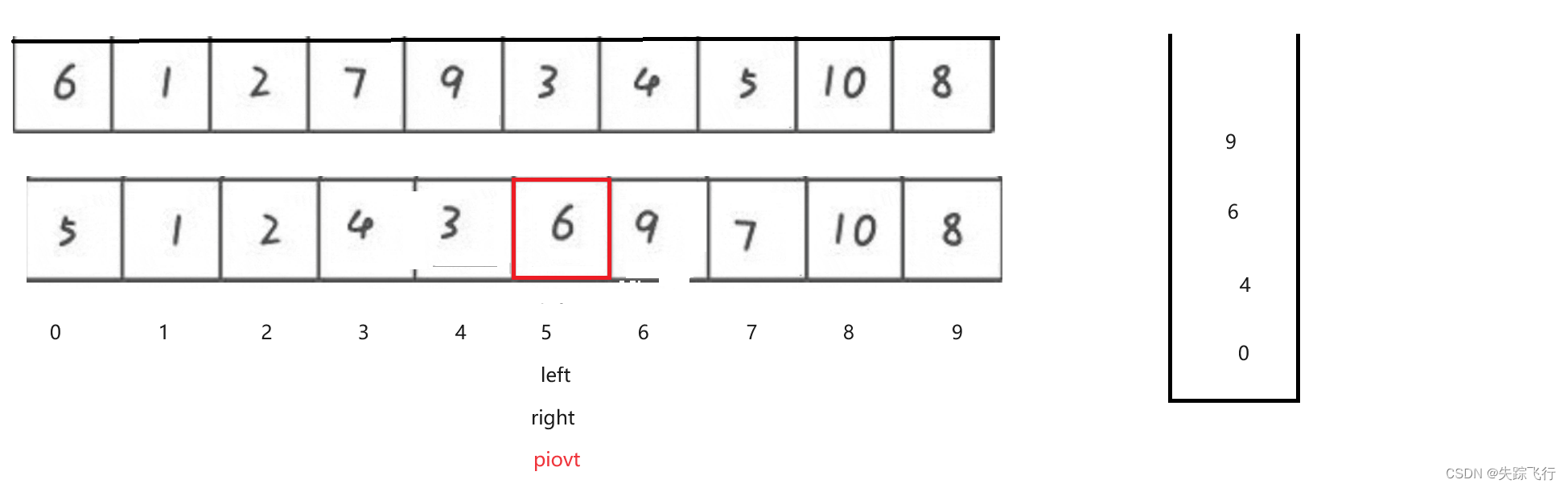
第一次弹出栈顶元素给到right在弹出栈顶元素给left.重新找基准值,找到后把基准值左右两边重新入栈,重复上述操作但当基准值左右两边只有一个元素的时候,就不需要再入栈,此时已经是有序的了,把最开始的基准值右边的排完后,排基准值左边的.,直到栈为空的时候,排完序.
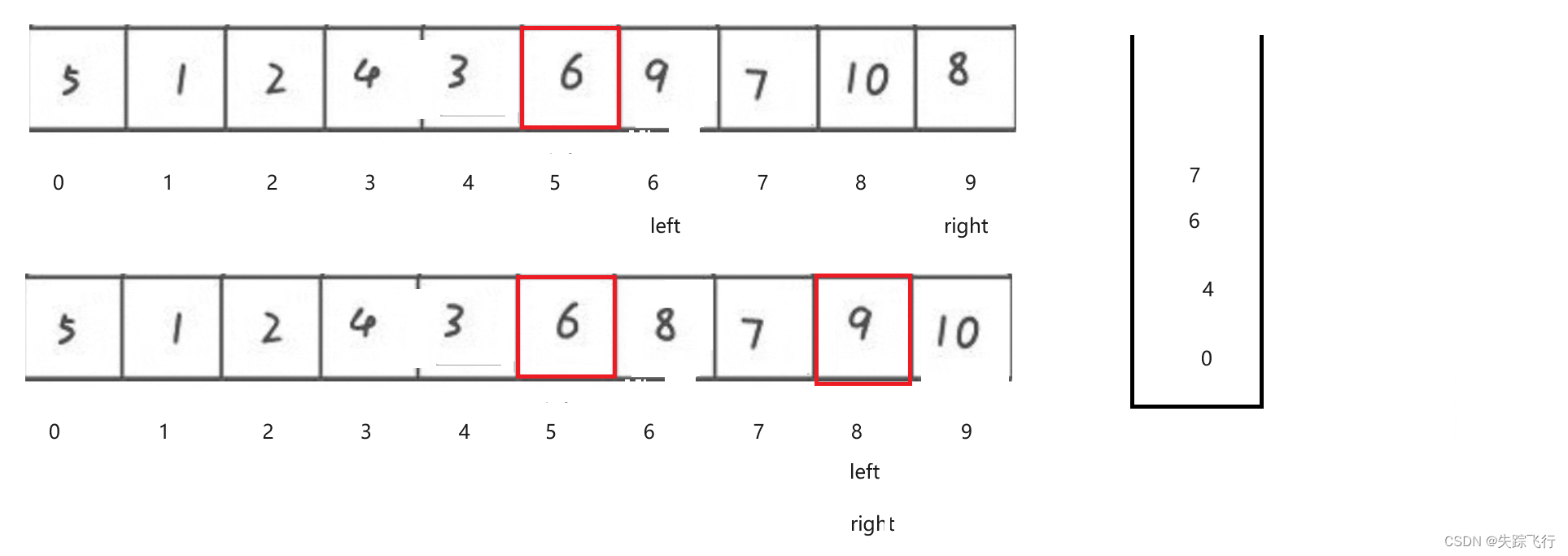第一次弹出栈顶元素给到right在弹出栈顶元素给left.重新找基准值,找到后把基准值左右两边重新入栈,重复上述操作但当栈为空的时候排序完成
public void quickSort(int[] array) {
Deque<Integer> stack = new LinkedList<>();
int left = 0;
int right = array.length - 1;
int pivot = partition(array,left,right);
if(pivot > left + 1) {
stack.push(left);
stack.push(pivot -1);
}
if(pivot < right- 1) {
stack.push(pivot+ 1);
stack.push(right);
}
while(!stack.isEmpty()) {
right = stack.pop();
left = stack.pop();
pivot = partition(array,left,right);
if(pivot > left + 1) {
stack.push(left);
stack.push(pivot -1);
}
if(pivot < right- 1) {
stack.push(pivot+ 1);
stack.push(right);
}
}
}
private int partition(int[] array,int left,int right) {
int tmp = array[left];
while(left < right) {
while(left < right && array[right] >= tmp) {
right--;
}
array[left] = array[right];
while(left < right && array[left] <= tmp) {
left++;
}
array[right] = array[left];
}
array[left] = tmp;
return left;
}
}
七大排序算法复杂度及稳定性分析
