代码随想录第34天 | 343. 整数拆分 96.不同的二叉搜索树

news2024/10/7 13:03:24

343. 整数拆分

/**
 * @param {number} n
 * @return {number}
 */
var integerBreak = function(n) {
   let dp=new Array(n+1)
   dp.fill(1)
   for(let i=3;i<=n;i++)
    for(let j=1;j<=i/2;j++){
       dp[i]= max(dp[i],max(j*(i-j),dp[i-j]*j))
    }
function max(a,b){
   return a>=b?a:b
}
    return dp[n]
};

想法

1.dp[i]：分拆数字i，可以得到的最大乘积为dp[i]。

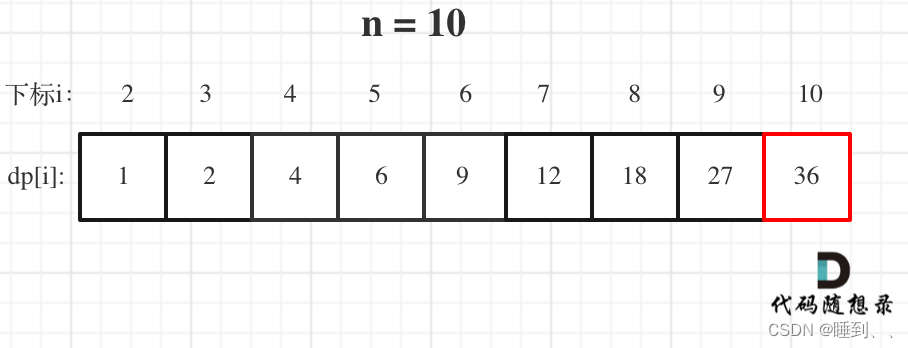
在这里插入图片描述

2.为什么不是 dp[i] = dp[i-j]*dp[j],这段代码写起来，也行

class Solution {
public:
    int integerBreak(int n) {
        if (n <= 3) return 1 * (n - 1);
        vector<int> dp(n + 1, 0);
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 3;
        for (int i = 4; i <= n ; i++) {
            for (int j = 1; j <= i / 2; j++) {
                dp[i] = max(dp[i], dp[i - j] * dp[j]);
            }
        }
        return dp[n];
    }
};

在这里插入图片描述

3. 递推公式：dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));

(i - j) * j？

因为dp[3]的dp[2]1=1,，小于21=2

dp[i - j] * j

相当于是拆分(i - j) ,j是从1开始遍历，拆分j的情况，在遍历j的过程中其实都计算过了。

法二

本题也可以用贪心，每次拆成n个3，如果剩下是4，则保留4，然后相乘，但是这个结论需要数学证明其合

class Solution {
public:
    int integerBreak(int n) {
        if (n == 2) return 1;
        if (n == 3) return 2;
        if (n == 4) return 4;
        int result = 1;
        while (n > 4) {
            result *= 3;
            n -= 3;
        }
        result *= n;
        return result;
    }
};

困难

收获

96.不同的二叉搜索树

/**
 * @param {number} n
 * @return {number}
 */
var numTrees = function(n) {
      const dp = new Array(n + 1).fill(0)
        dp[0]=1
        for (let i = 1; i <= n; i++) {
            for (let j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j]
            }
          // console.log("dp["+i+"]="+dp[i])
        }
        return dp[n]
};