图像特征提取
- 一、颜色特征
- 量化颜色直方图
- 聚类颜色直方图
- 二、边缘特征
- 边缘
- 边缘定义
- 边缘提取
- 边缘精细
- 三、特征点的特征描述子
- Harris角点
- FAST角点
- 斑点
- SIFT
- Haar-like特征
- SURF
- ORB
- LBP
- Gabor
一、颜色特征
量化颜色直方图
HSV空间
优势:计算高效
劣势:量化问题,稀疏
聚类颜色直方图
使用颜色空间:Lab颜色空间
操作:
- 使用聚类算法对所有像素点颜色向量进行聚类
- 单元用聚类代表
二、边缘特征
边缘
像素明显变化的区域
具有丰富的语义信息
用于:物体识别、几何、视角变换
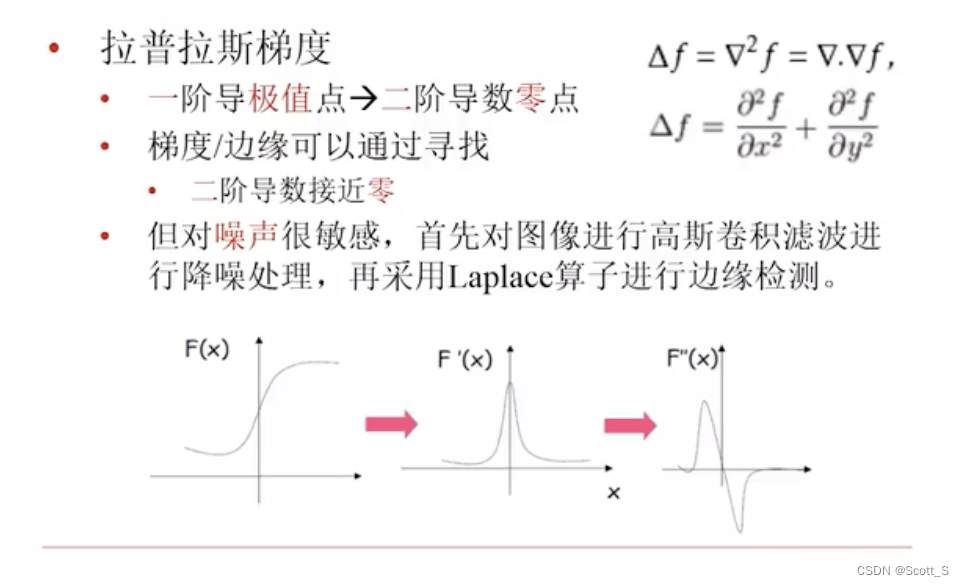
边缘定义
- 像素值快速变化的区域
- 一阶导数的极值
边缘提取
一、做法
先做高斯去燥,再使用一阶导数获取机制
原因:一阶导数对噪声敏感
二、场景
横竖:一阶导数
斜的:梯度,分别对x和y分别求导


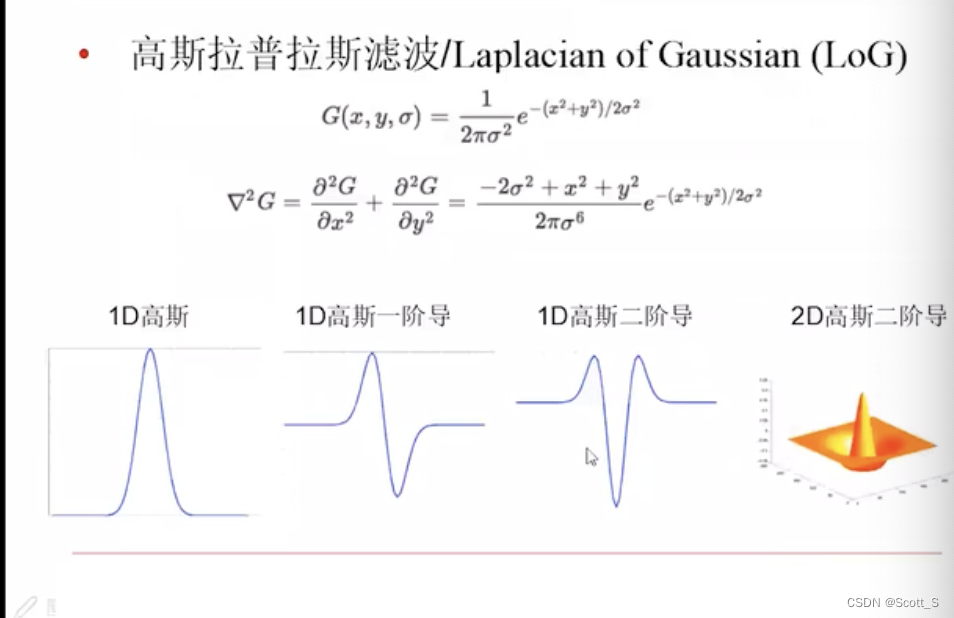
边缘精细
影像因素:高斯,x,y方向参数问题
不同标准差的滤波,能提取不同尺寸的边缘。
三、特征点的特征描述子

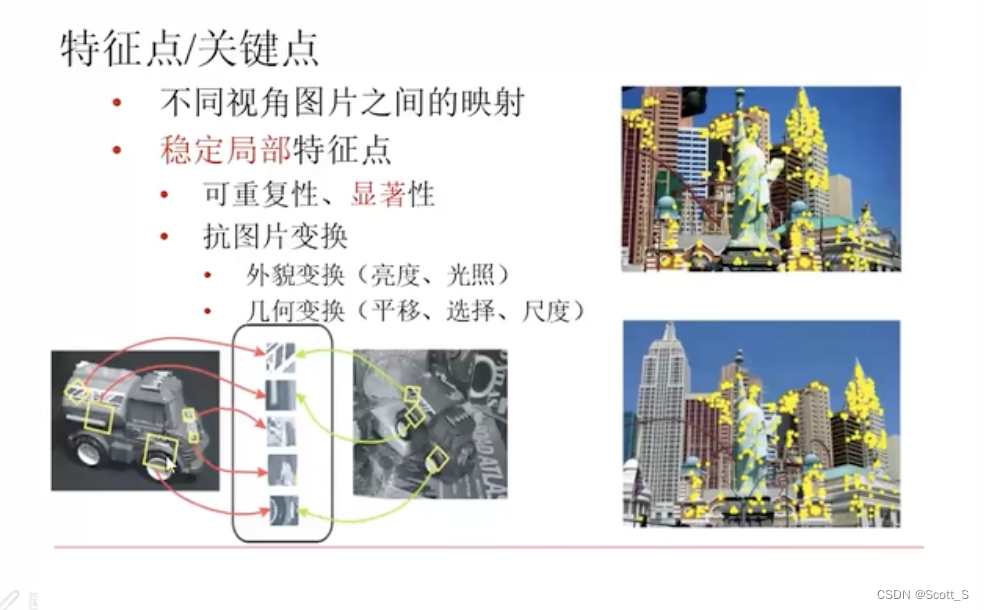
Harris角点
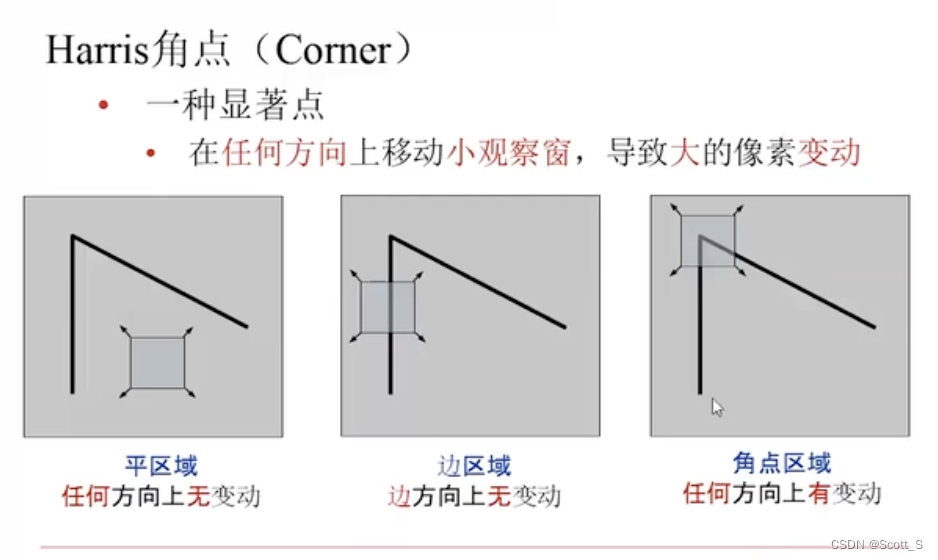
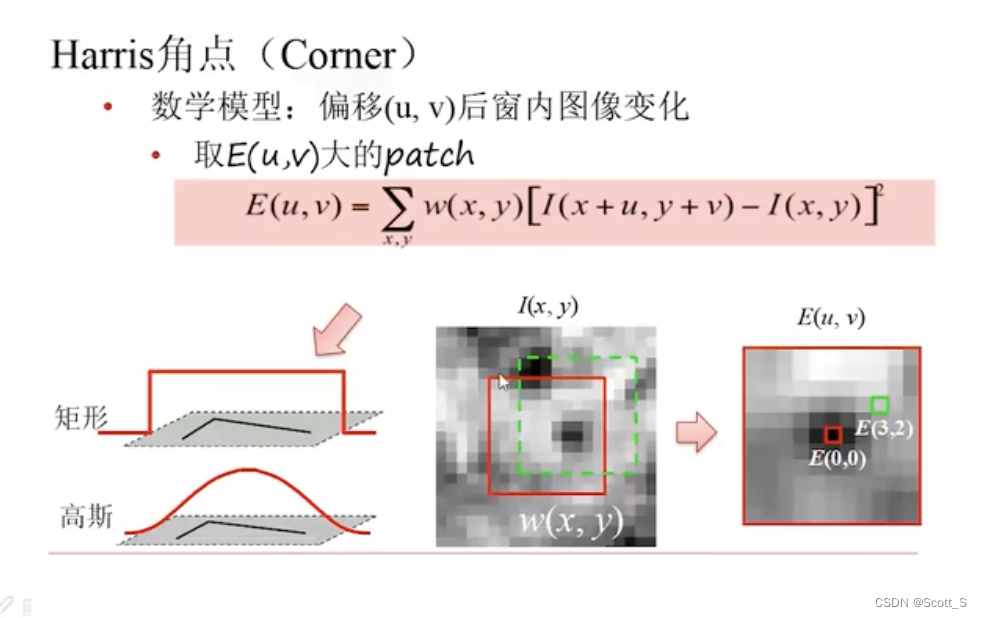
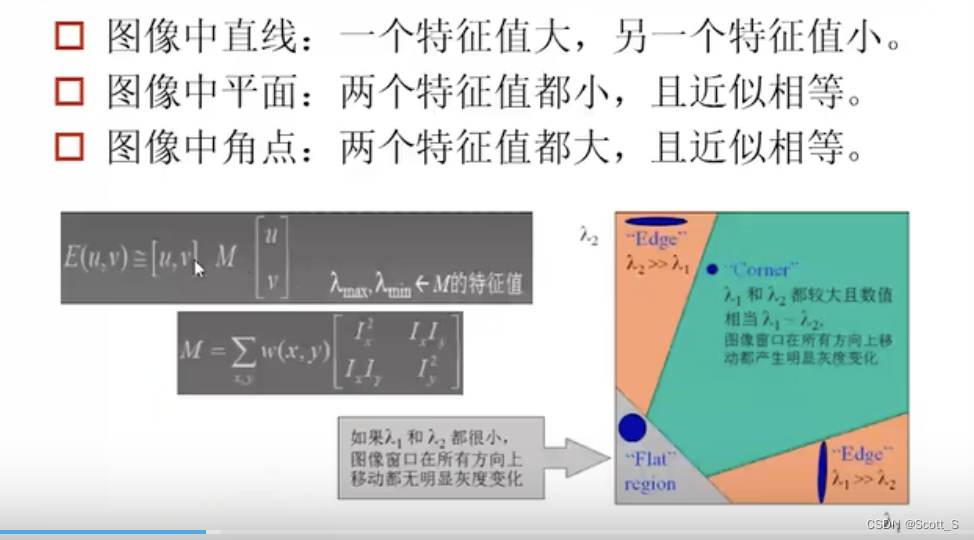

FAST角点

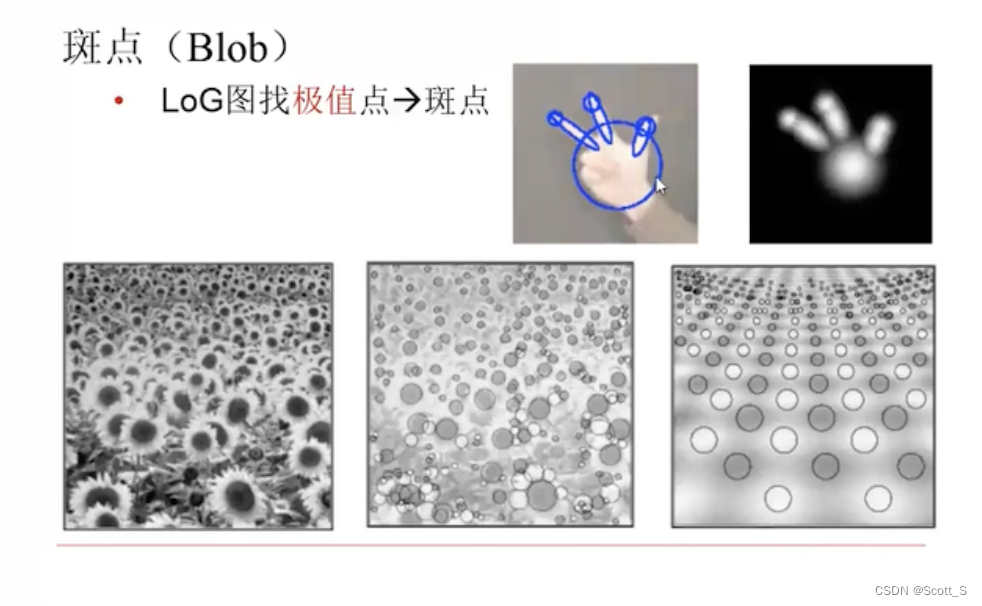
斑点

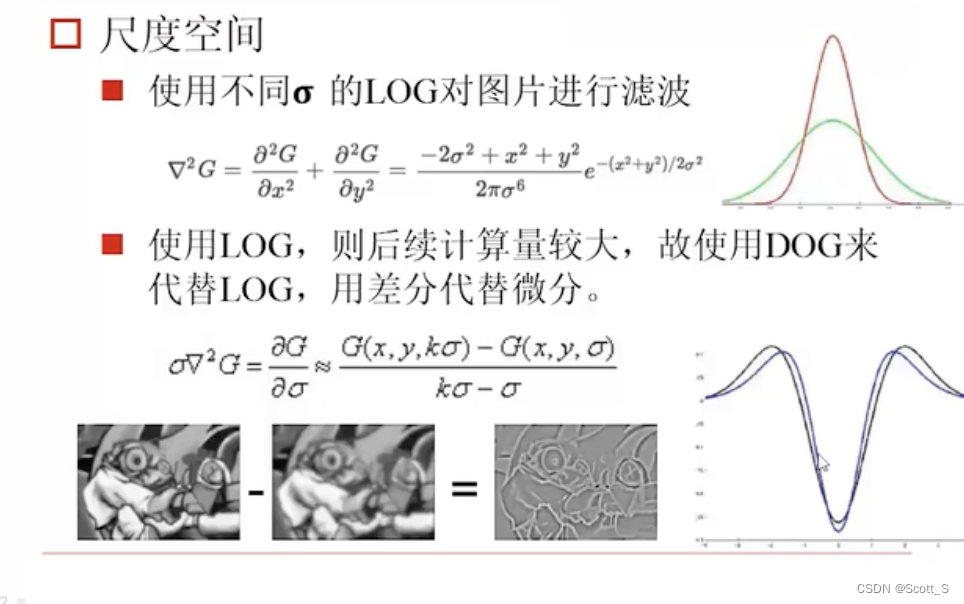
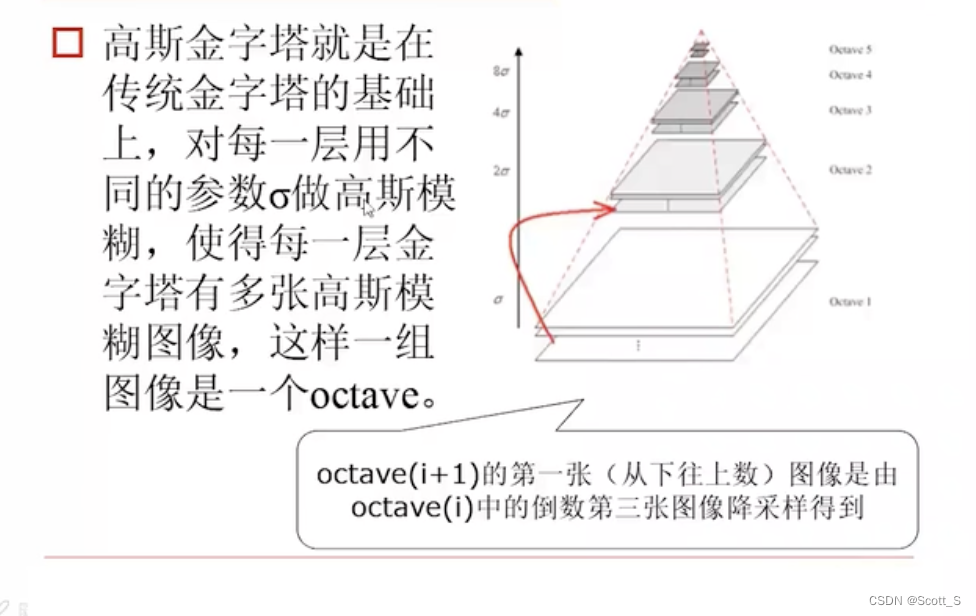
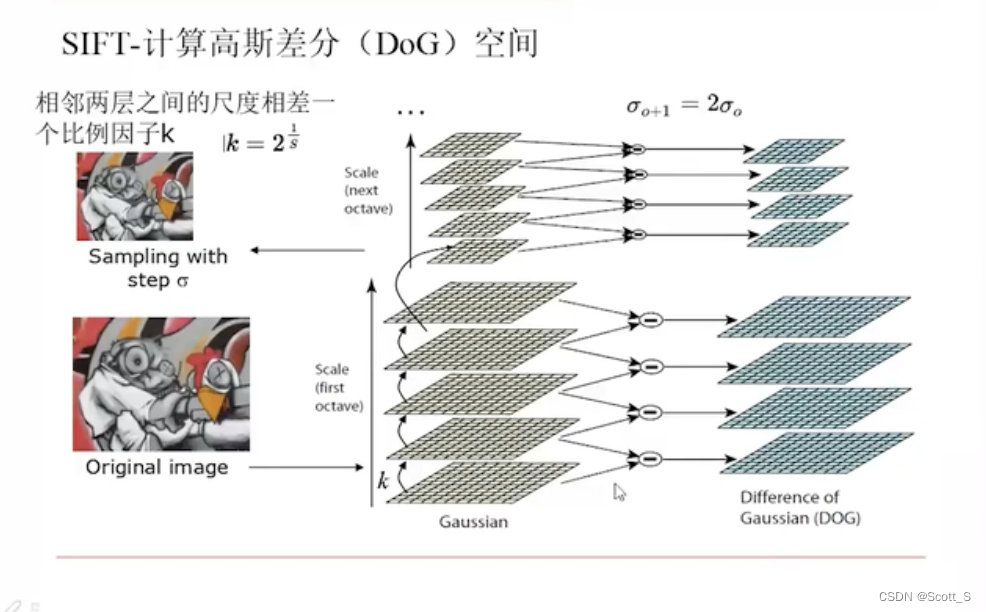
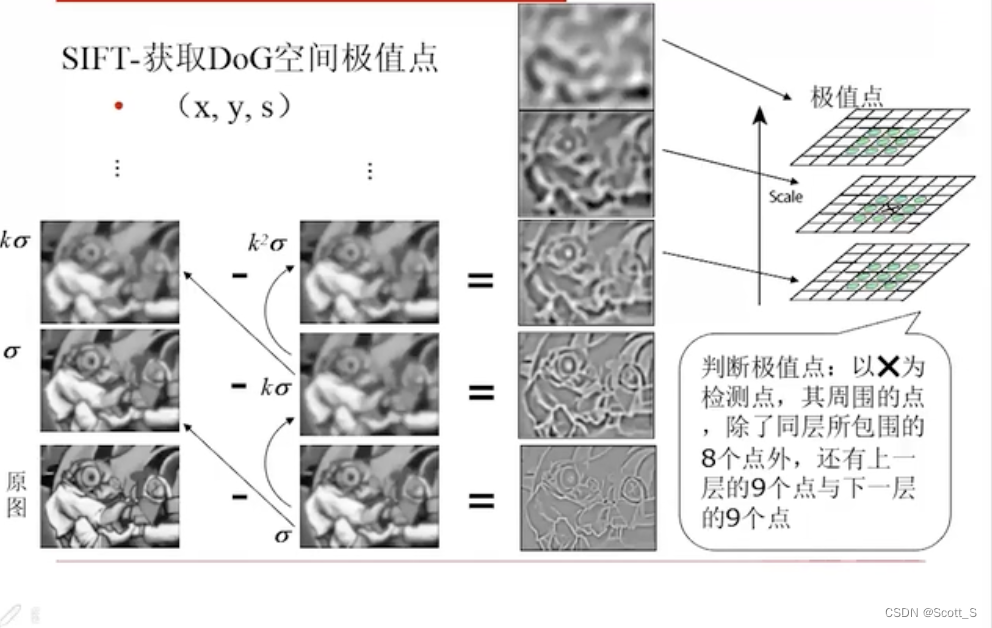
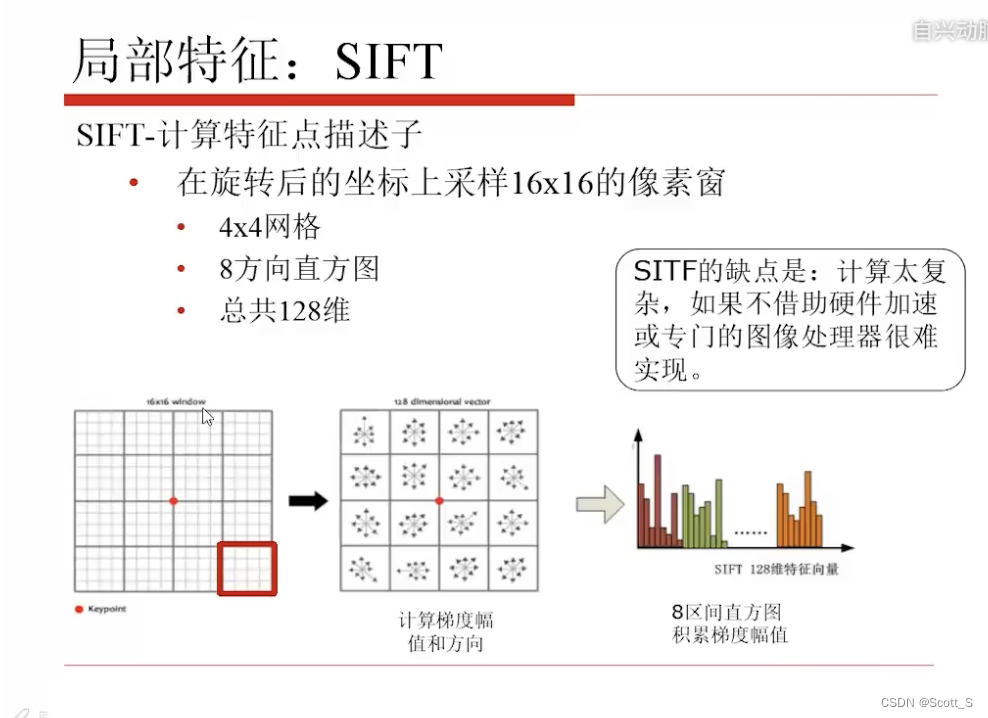
SIFT
基于尺度空间不变的特征
特点:
- 具有良好的不变性【旋转、尺度缩放、平移、亮度、视角变化、仿射变换、噪声也有一定积极的稳定性
- 独特性好,信息量丰富
- 多量性:即使少数物体也可以产生大量SIFT特征
- 计算快,SIFT匹配算法可以达到实时性。

- 找极值点
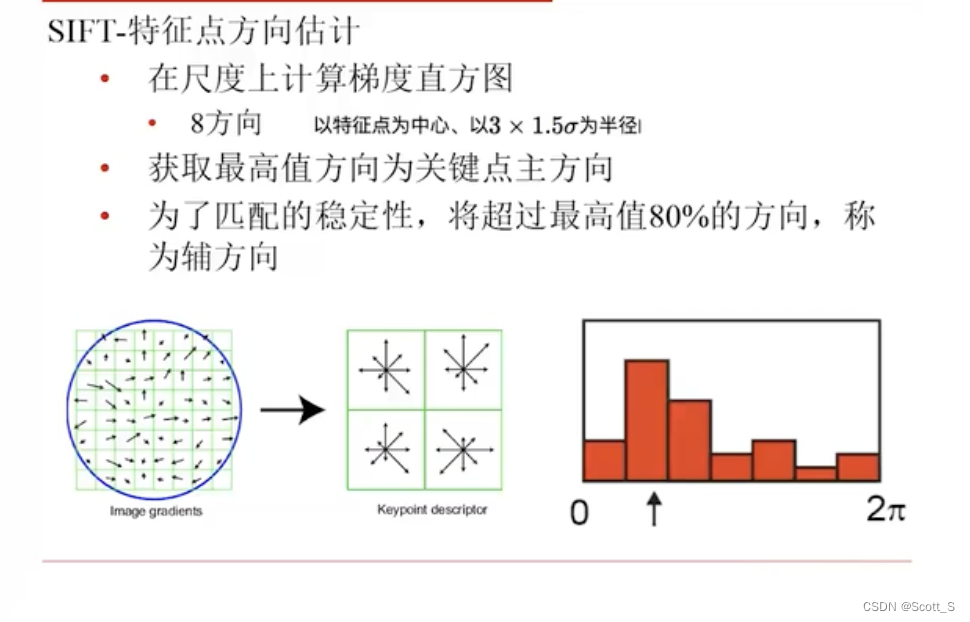
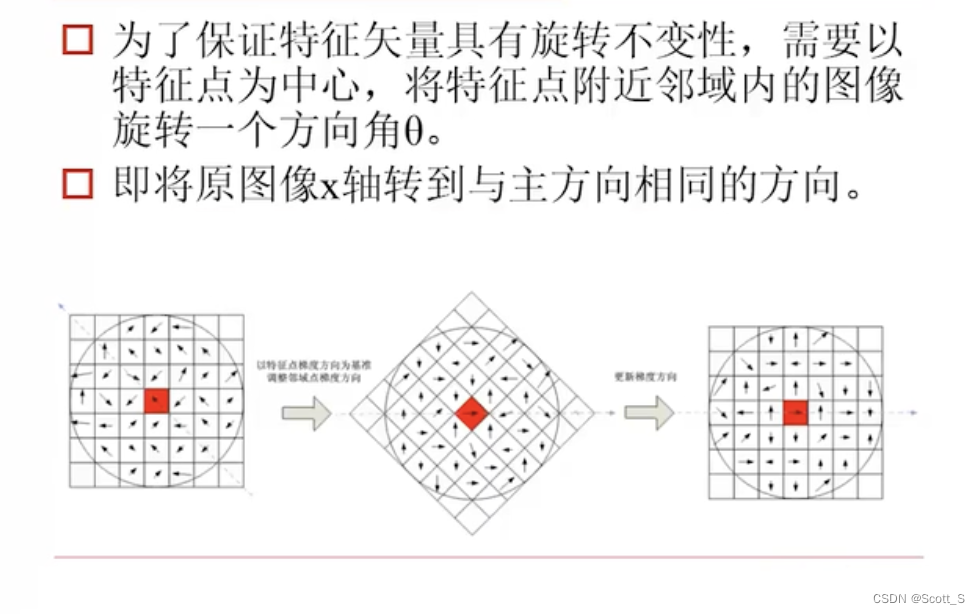
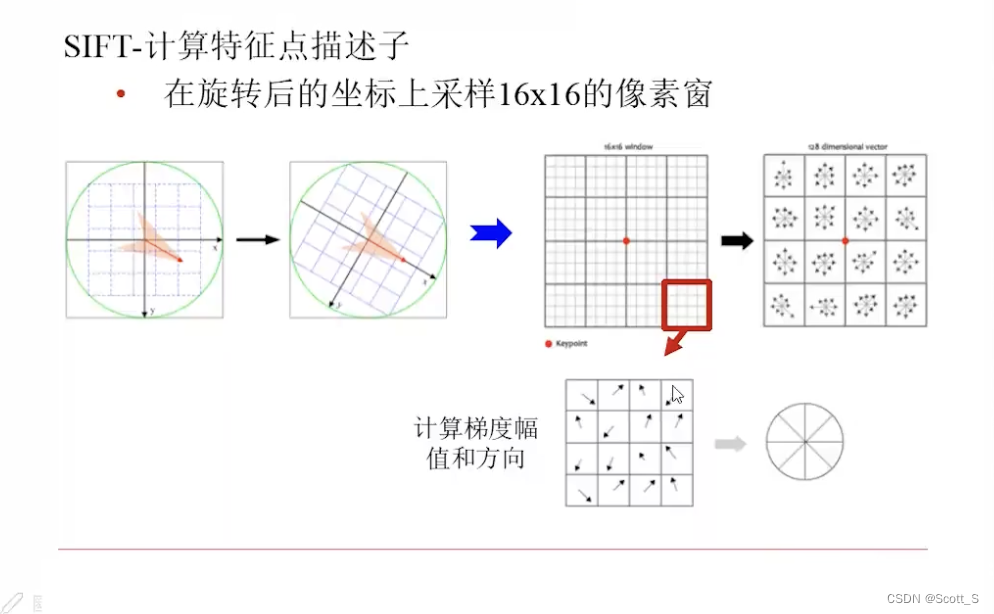
- 找主方向
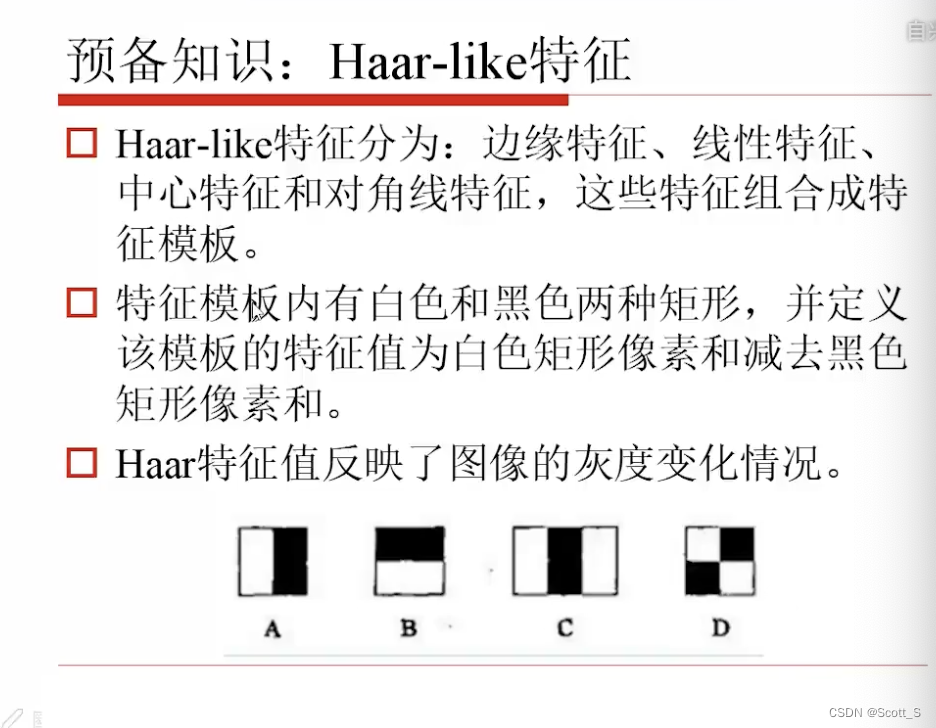
Haar-like特征
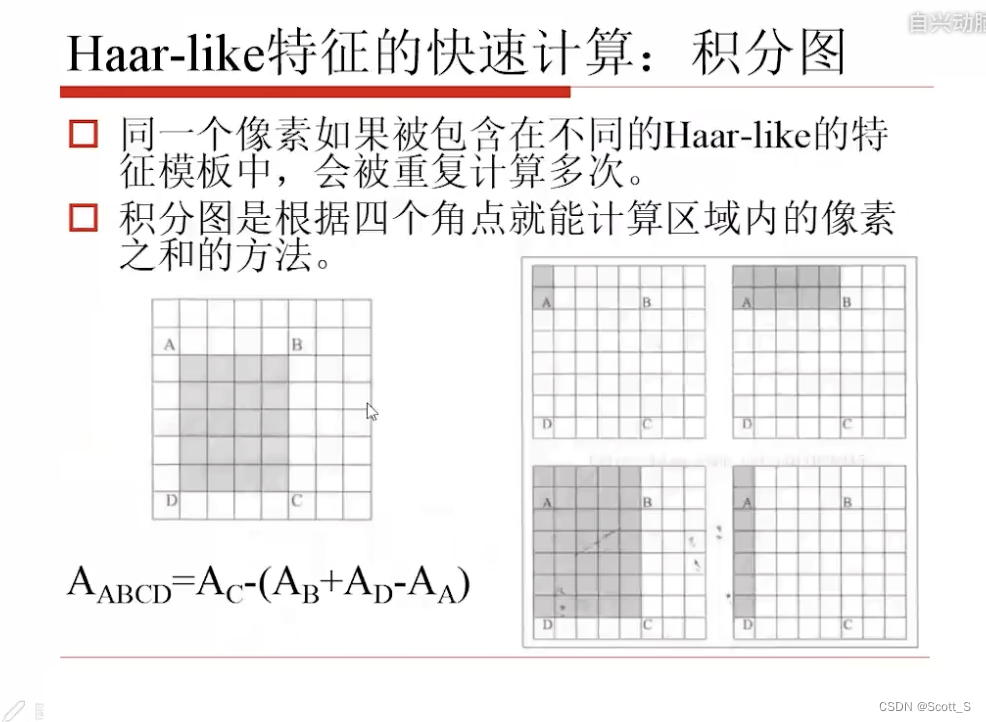
SURF

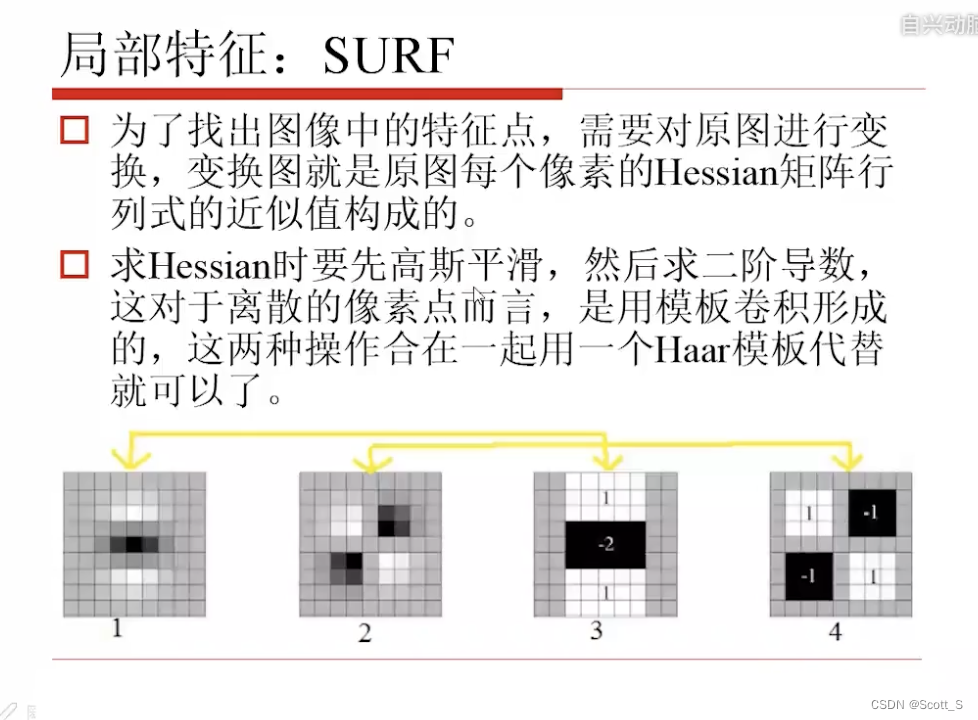
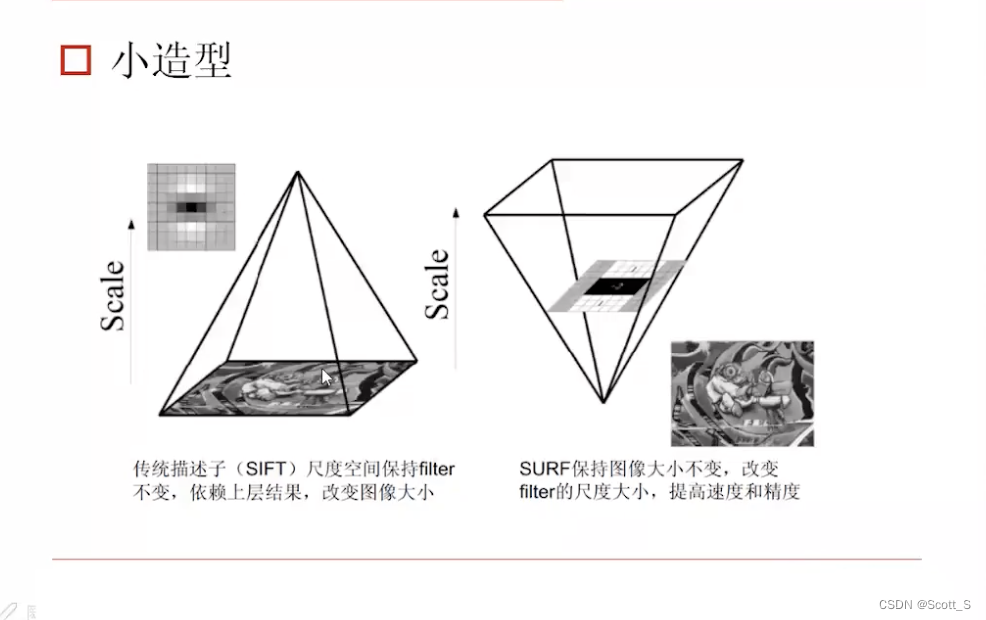
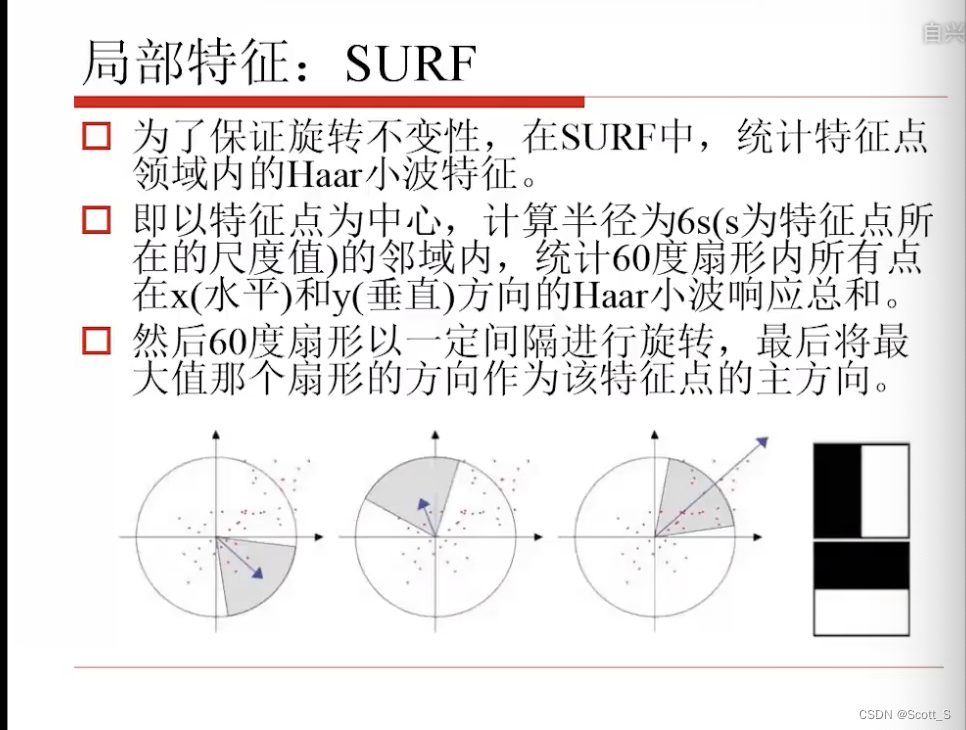
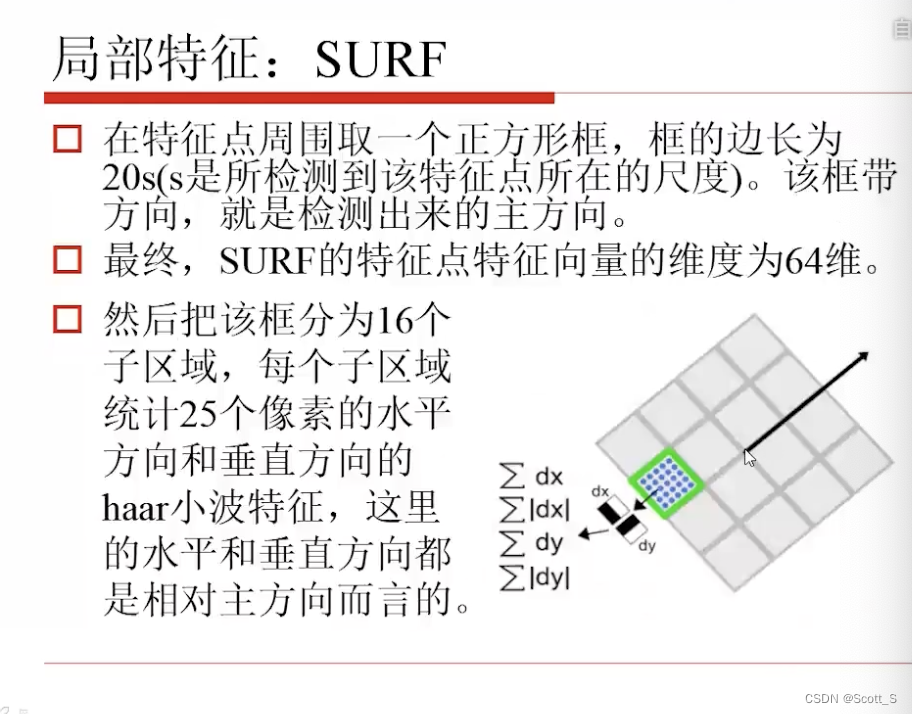

ORB



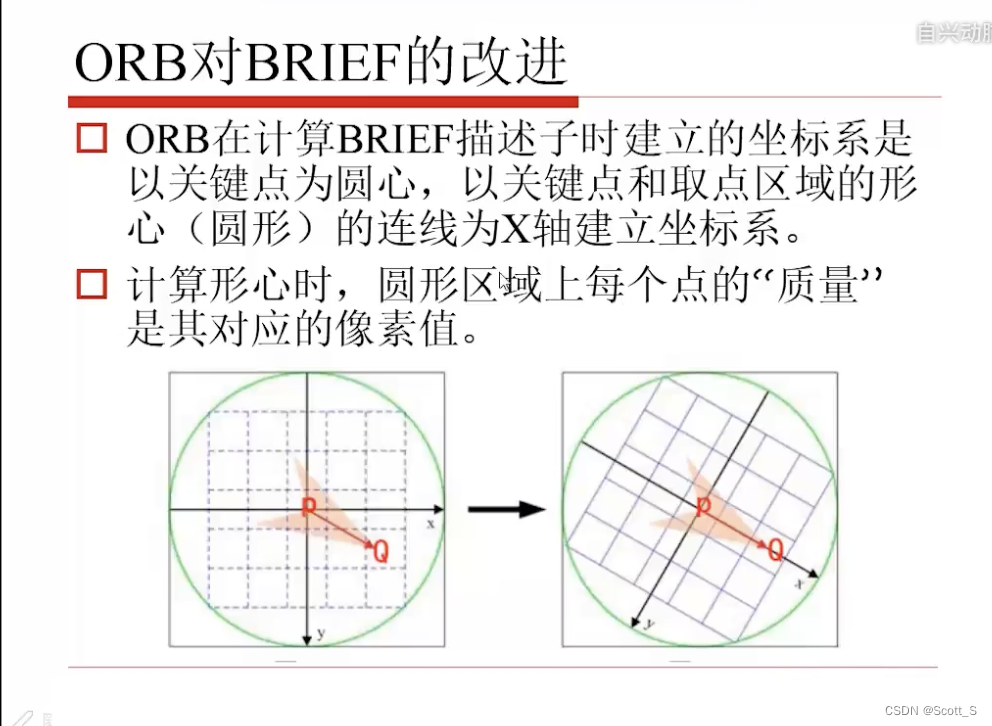
LBP
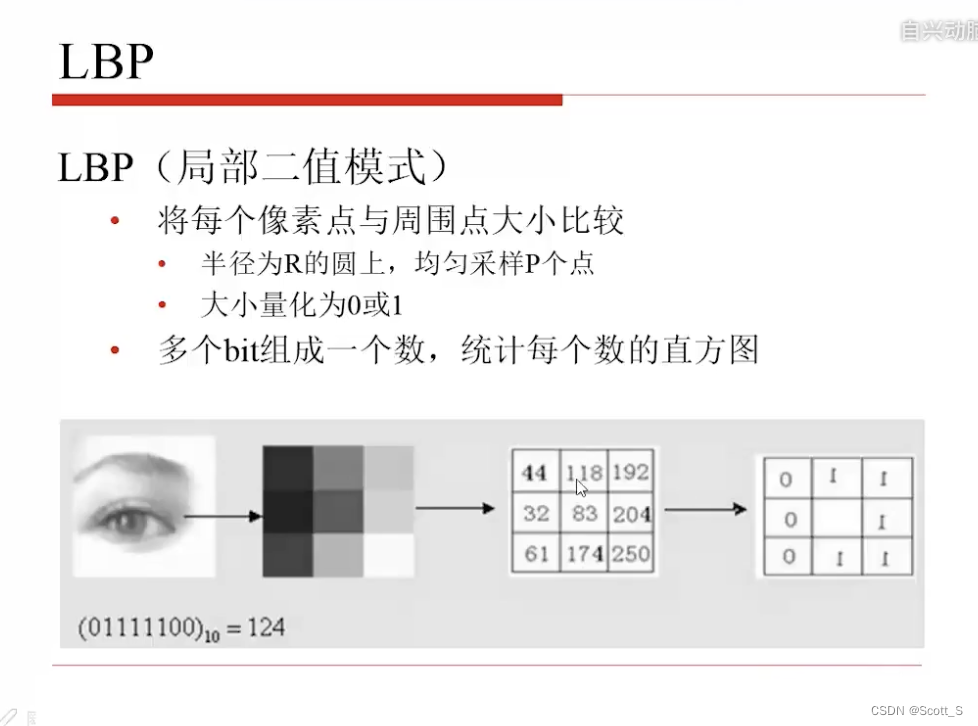
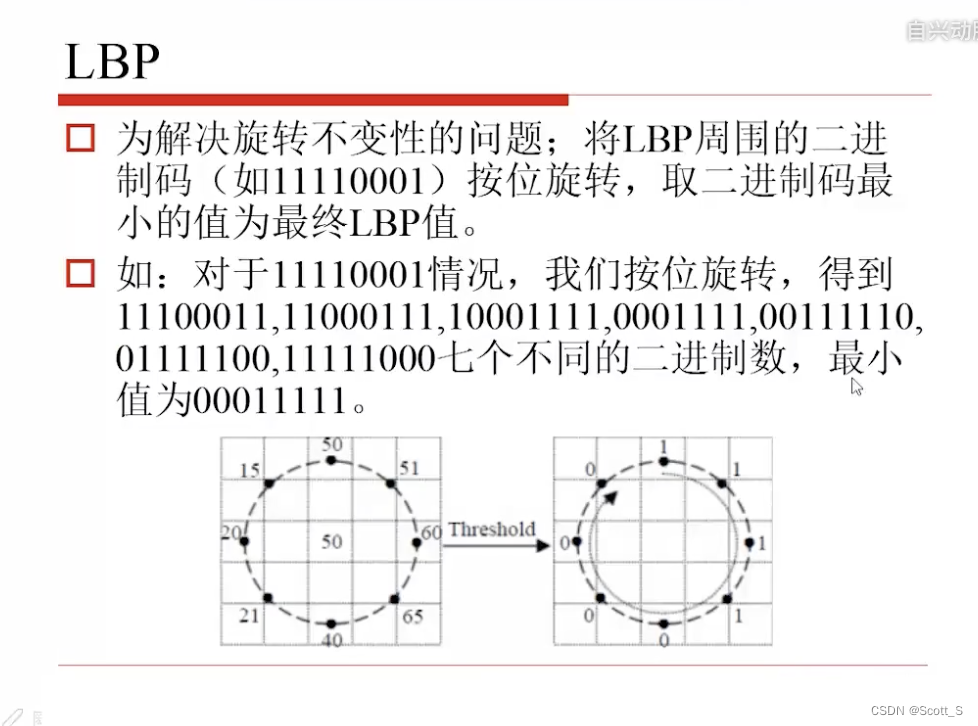
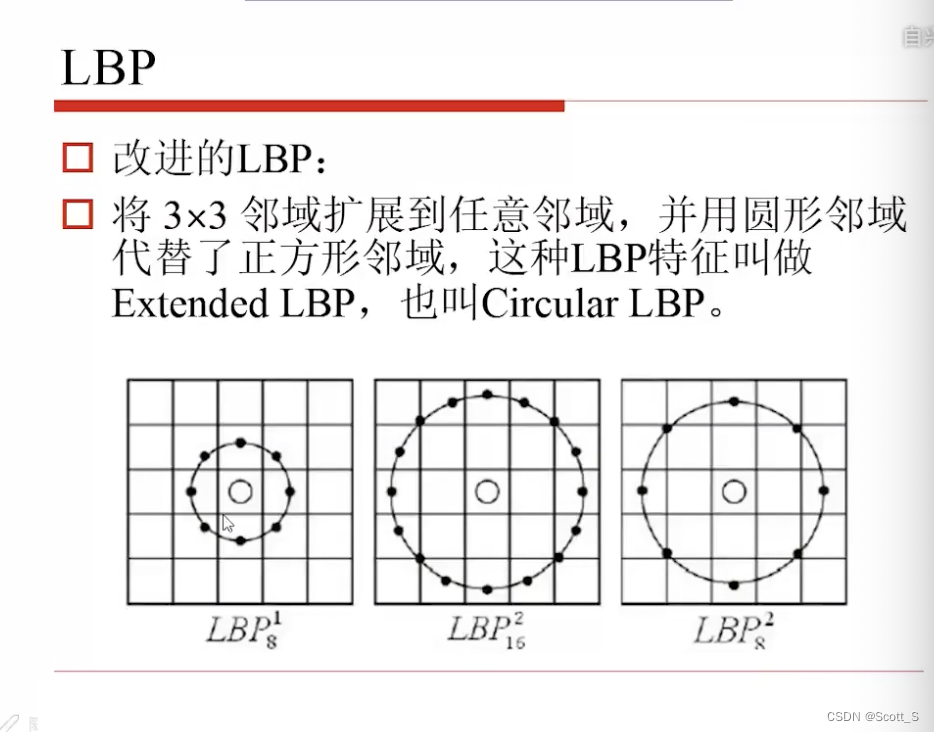
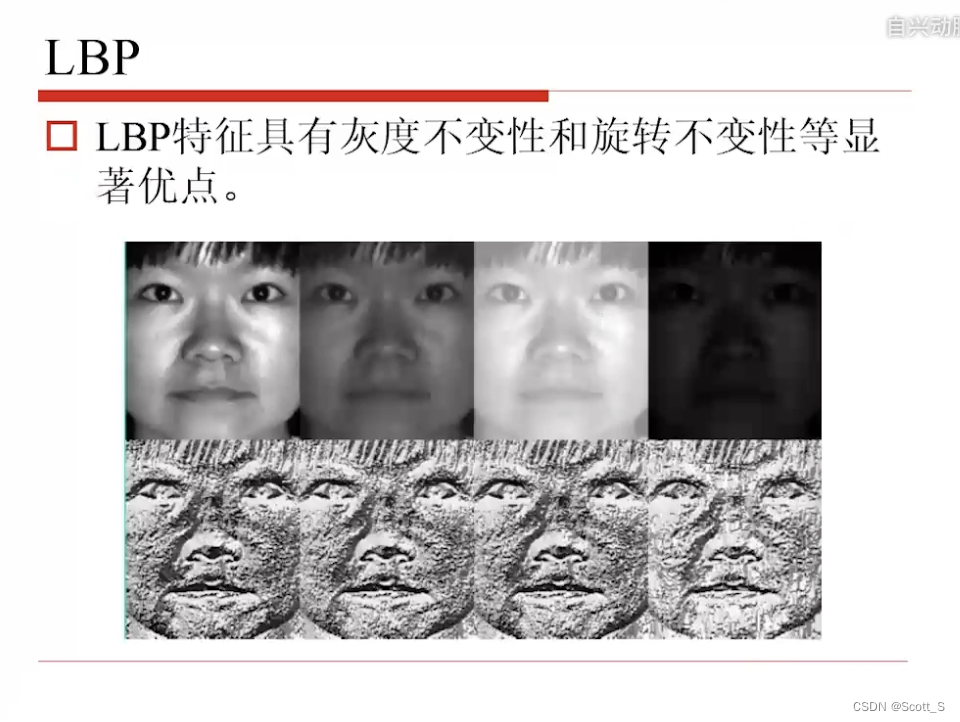
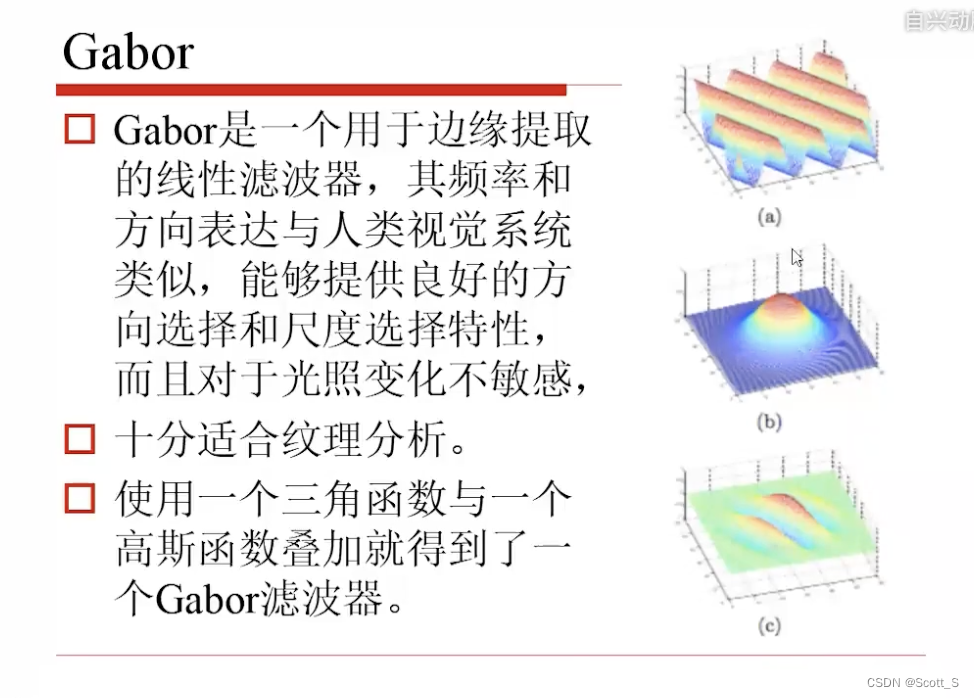
Gabor