给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:

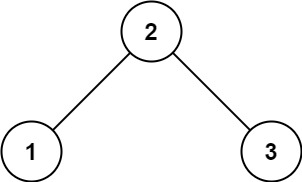
输入: root = [2,1,3]
输出: 1

示例 2:

输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
        //层序迭代
        //记录每一行的第一个元素，从左往右
        //或者从右往左，最后一个遍历的就是ans
        queue<TreeNode*>que;
        int ans = 0;
        if(!root) return 0;
        que.push(root);
        while(!que.empty()){
            int size = que.size();
            while(size--){
                TreeNode* node = que.front();
                que.pop();
                if(node->right) que.push(node->right);
                if(node->left) que.push(node->left);
                ans = node->val;
            }
        }
        return ans;
    }
};
//迭代bfs，从左往右遍历
class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
        //层序迭代
        //记录每一行的第一个元素，从左往右
        //或者从右往左，最后一个遍历的就是ans
        queue<TreeNode*>que;
        int ans = 0;
        if(!root) return 0;
        que.push(root);
        while(!que.empty()){
            int size = que.size();
            for(int i = 0;i < size;i++){
                TreeNode* node = que.front();
                que.pop();
                if(i == 0) ans = node->val;
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
        }
        return ans;
    }
};
//dfs
class Solution {
public:
    int maxnum = INT32_MIN;
    int res = 0;
    void dfs(TreeNode* root,int depth){
        if(!root) return;
        if(!root->left && !root->left){
            if(depth > maxnum){
                maxnum = depth;
                res = root->val;
            } 
        }
        if(root->left) dfs(root->left,depth+1);//此处隐藏着回溯
        //第二层，d=1。符合到第三层 d=2，不符合，然后max记录一下，val记录
        //回到第二层，在回到第一层，d=0。进入右边第一层同理。
        if(root->right) dfs(root->right,depth+1);
    }
    int findBottomLeftValue(TreeNode* root) {
        //dfs
        int depth = 0;
        if(!root) return 0;
        dfs(root,depth);
        return res;
    }
};
//dfs,第二个版本
class Solution {
public:
    int maxnum = INT32_MIN;
    int res;
    void dfs(TreeNode* root,int depth){
        if(!root->left && !root->right){
            if(depth > maxnum){
                maxnum = depth;
                res = root->val;
            }
            return; 
        }
        if(root->left){
            depth++;
            //在这里dep改变了。而dfs(root->left,dep+1)，dep//并没有改变，改变的只是传入下一层的dep变化，并没有改变当前层。
            dfs(root->left,depth);
            depth--; // 回溯。得到多少，为了符合条件就得减掉多少
        }
        if(root->right){
            depth++;
            dfs(root->right,depth);
            depth--;
        }
    }
    int findBottomLeftValue(TreeNode* root) {
        //dfs
        int depth = 0;
        dfs(root,depth);
        return res;
    }
};