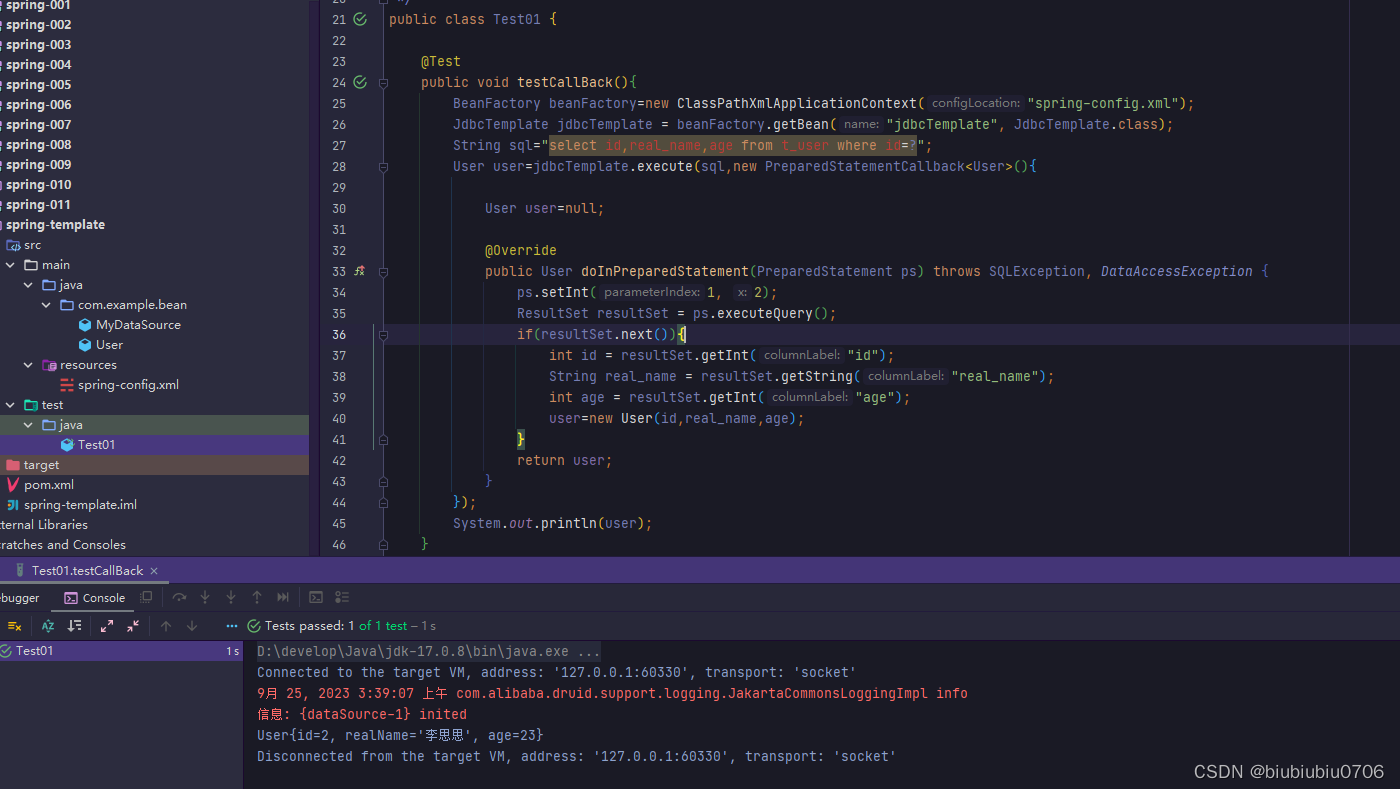
文章目录
- 一、图像几何变换理论
- 二、图像平移
-
- 2.1 使用数学公式的实现方式为:
- 2.2 使用矩阵实现的方式为
- 2.3 使用opencv
- 三、图像缩放
-
- 3.1 用数学式子表示为公式(a为缩放系数):
- 3.2 用矩阵表示如公式所示:
一、图像几何变换理论
图像几何变换不改变图像的像素值,在图像平面上进行像素变换。适当的几
何变换可以最大程度地消除由于成像角度、透视关系乃至镜头自身原因所造成的
几何失真所产生的负面影响。几何变换常常作为图像处理应用的预处理步骤,是
图像归一化的核心工作之一[1]。
一个几何变换需要两部分运算:
- 空间变换:包括平移、缩放、旋转和正平行投影等,需要用它来表示输
出图像与输入图像之间的像素映射关系。 - 灰度插值算法:按照这种变换关系进行计算,输出图像的像素可能被映
射到输入图像的非整数坐标上[2]。
图像几何变换在变换过程中会建立一种原图像像素与变换后图像像素之间的映射关系,通过这种关系,能够从一方的像素计算出另一方的像素的坐标位置。通常将图像坐标映射到输出的过程称作向前映射,反之,将输出图像映射到输入的过程称作向后映射。向后映射在实践中使用较多,原因是能够避免使用向前映射中出现映射不完全和映射重叠的问题。
对于数字图像而言,像素的坐标是离散型非负整数,但是在进行变换的过程
中有可能产生浮点坐标值。这在图像处理中是一个无效的坐标。为了解决这个问
题需要用到插值算法。常见算法如下:
- 最近邻插值
- 双线性插值
- 双立方插值
图像变换是建立在矩阵运算基础上,通过矩阵运算可以很快找到对应关系。绍常见的图像几何变换,包括图形平移、图像缩放、图像旋转、图像镜像、图像仿射、图像透视等。
二、图像平移
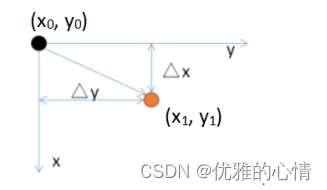
图像平移是将图像中的所有像素点按照给定的平移量进行水平或垂直方向上的移动。假设原始像素的位置坐标为(x0,y0),经过平移量(△x,△y)后,坐标变为(x1, y1),如图所示:
用数学式子表示为公式,△x 和△y 称为平移量:
x 1 = x 0 + Δ x \mathrm{x}_{1}=\mathrm{x}_{0}+\Delta \mathrm{x} x1=x0+Δx
y 1 = y 0 + Δ y \mathrm{y}_{1}=\mathrm{y}_{0}+\Delta \mathrm{y} y1=y0+Δy
2.1 使用数学公式的实现方式为:
def translate_img(img, move_y, move_x):
h, w, c = img.shape
translated_img = np.zeros((h, w, c), dtype=np.uint8)
for i in range(h):
for j in range(w):
if i >= move_y and j >= move_x:
translated_img[i, j] = img[i - move_y, j - move_x]
return translated_img
2.2 使用矩阵实现的方式为
用矩阵表示如公式所示:
[ x 1 y 1 1 ] = [ x 0 y 0 1 ] [ 1 0 0 0 1 0 Δ x Δ y