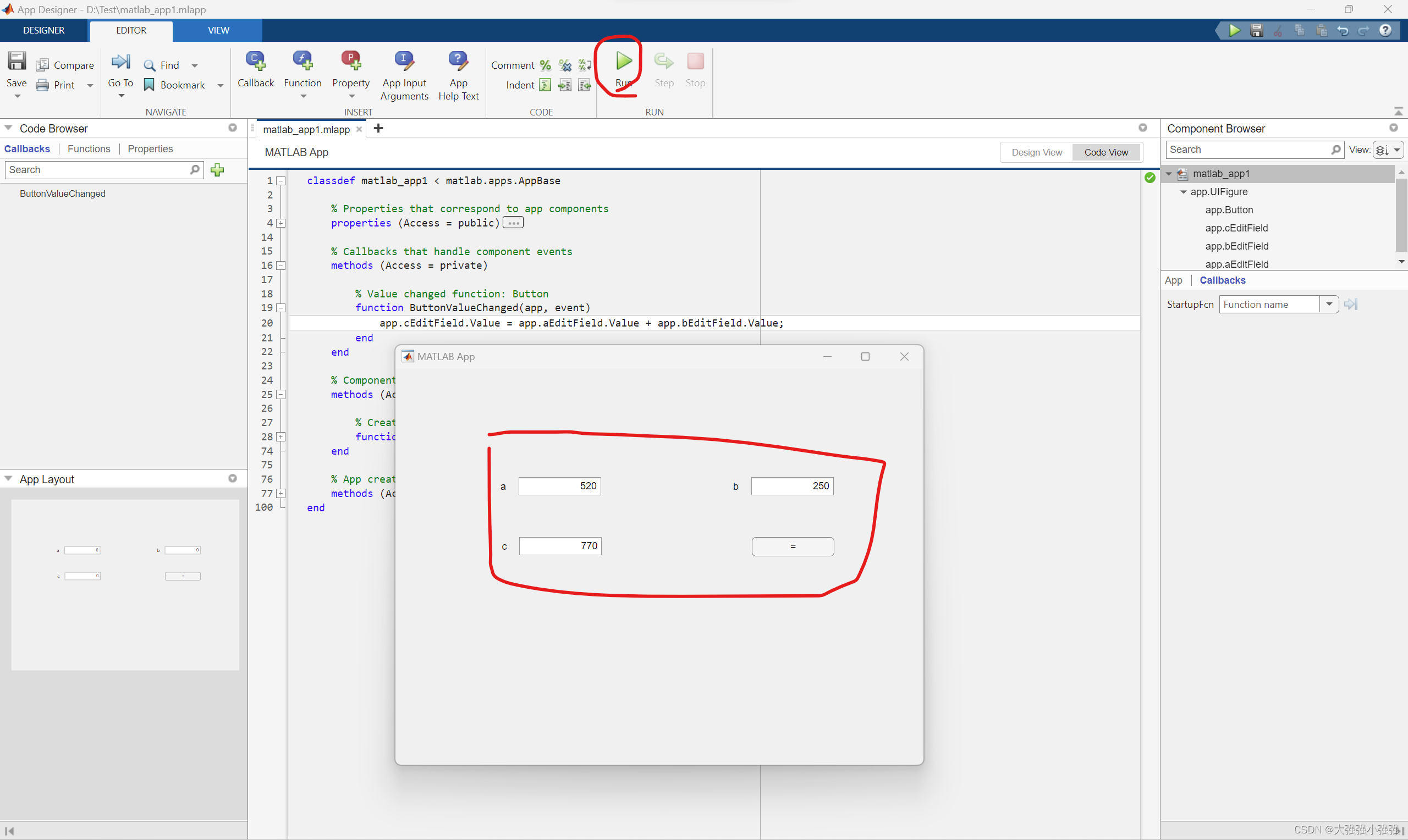
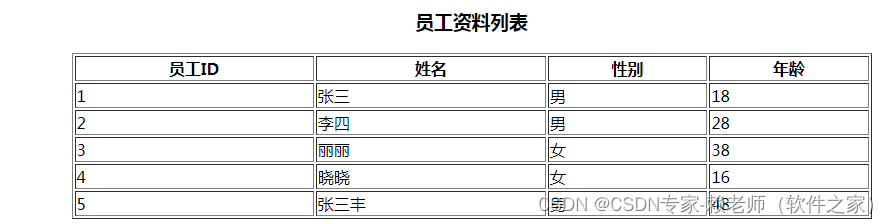
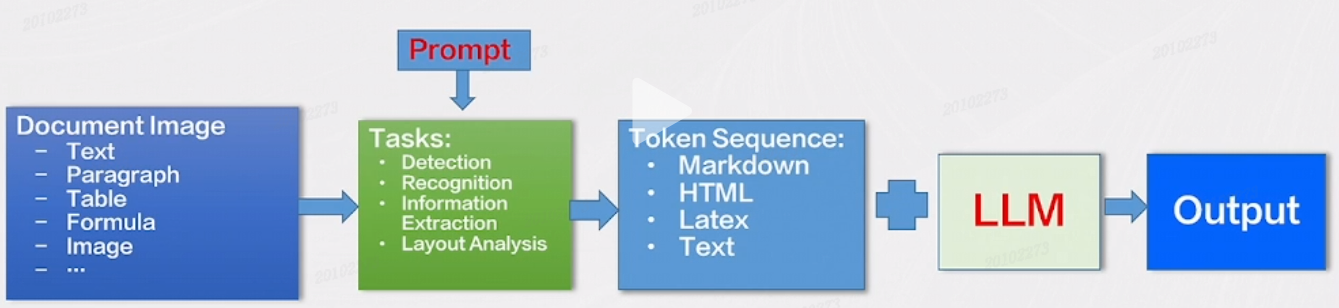
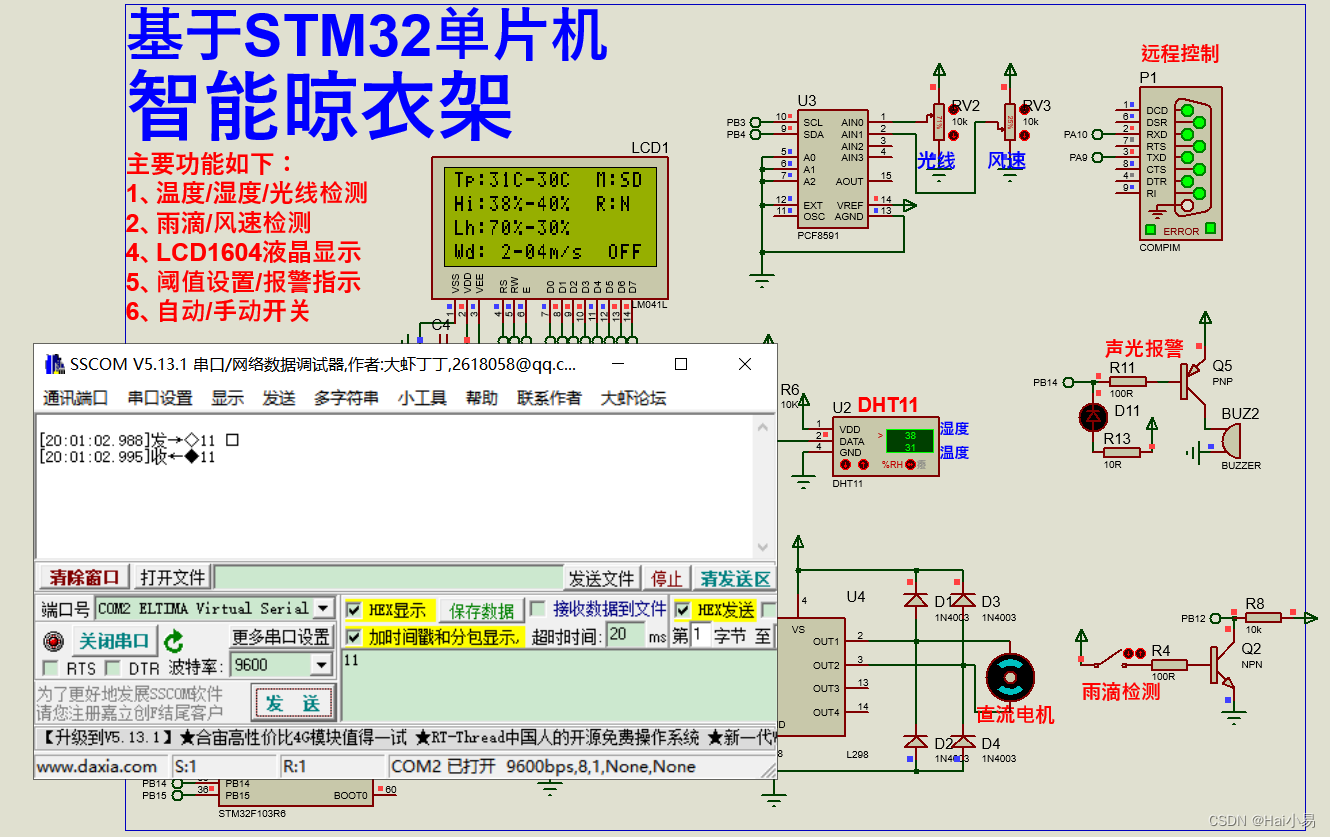
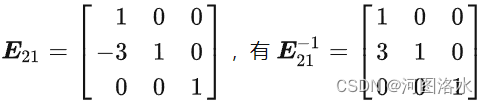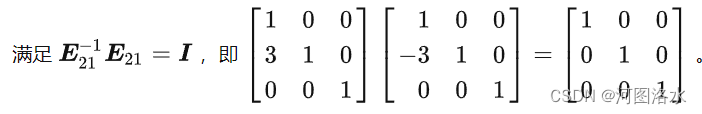一, 消元法 Method of Elimination
消元法是计算机软件求解线形方程组所用的最常见的方法。任何情况下,只要是矩阵A可逆,均可以通过消元法求得Ax=b的解
eg:
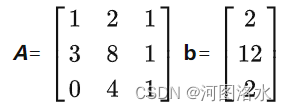
我们将矩阵左上角的1称之为“主元一”(the first pivot),第一步要通过消元将第一列中除了主元之外的数字均变化为0。操作方法就是用之后的每一行减去第一行的适当倍数,此例中第二行应减去第一行的3倍。之后应对第三行做类似操作,本例中三行第一列数字已经为0,故不用进行操作\

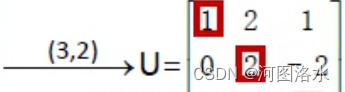
处在第二行第二列的主元二为2,因此用第三行减去第二行的两倍进行消元,得到第三个主元为5。
矩阵A为可逆矩阵,消元结束后得到上三角阵U(Uppertriangular matrix),其左侧下半部分的元素均为0,而主元1,2,5分列在U的对角线上。
Pivot cannot be 0 主元不能为0,如果恰好消元至某行,0出现在了主元的位置上,应当通过与下方一行进行“行交换”使得非零数字出现在主元位置上。如果0出现在了主元位置上,并且下方没有对等位置为非0数字的行,则消元终止,并证明矩阵A为不可逆矩阵,且线性方程组没有唯一解。
二, 回代 Back-Substitution
做方程的高斯消元时,需要对等式右侧的b做同样的乘法和加减法。手工计算时比较有效率的方法是应用“增广矩阵”(augmented matrix),将b插入矩阵A之后形成最后一列,在消元过程中带着b一起操作。(Matlab是算完系数矩阵再处理b的)
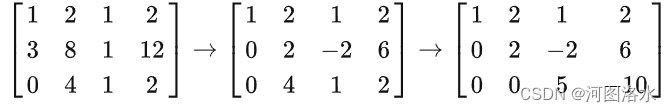
此时我们将原方程Ax=b转化为了新的方程Ux=c

从最后一行得到z=-2,依次回代可以得到y=1 和 x=2
三, 消元矩阵 Elimination Matrices
矩阵运算的核心内容就是对“行”或者“列”进行独立操作。
如前一节课“列图像”部分所言,系数矩阵乘以未知数向量,相当于对系数矩阵的列向量进行线性组合

matrix times a column is a column
combination of the columns of the matrix
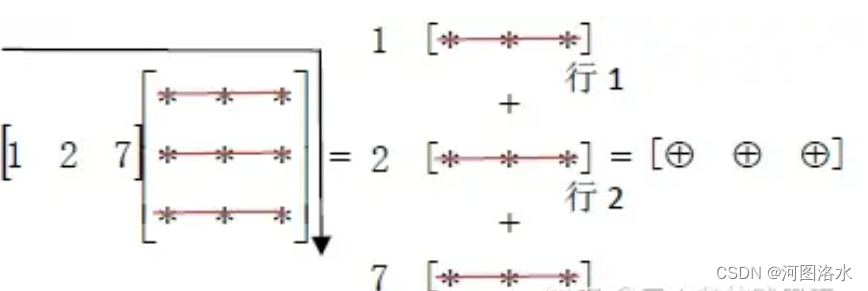
a row times matrix is a row
列向量的线性组合非常容易就接受了,左乘行向量这个总觉得很别扭,偏偏行向量在下面介绍消元矩阵时比较重要。后来想想觉得“列”操作就像是把向量开进矩阵,而“行操作”这个就像把向量倒车进入矩阵(如图中箭头所示)
Step 1 substract 3×row1 from row2
通过左乘矩阵E21来实现原矩阵A的第二行减去第一行的3倍这一过程。E21的第二行使矩阵A的行向量进行前述的线性组合,而其它两行为了保持与原矩阵相同,采用同阶单位阵I (identity matrix 和×1无区别)的行向量。左乘的这个矩阵为“初等矩阵”(Elementary Matrix),因此记做E。因为所乘行向量的倍数-3出现在E矩阵的第二行第一列,因此将之标注为21。完成操作后矩阵变为E21A

Step 2 substract 2×row2 from row3
矩阵消元的第二步是完成矩阵E21A的第三行减去第二行的2倍,通过左乘矩阵E32来实现这一过程
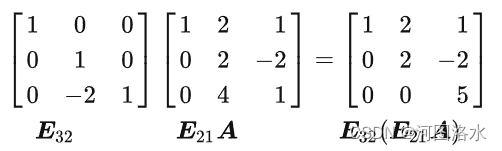
3x3矩阵的消元本来应该分三步完成,最终得到E32(E31(E21A))。本例中E31=I,所以结果变为E32(E21 A)=U,因为矩阵运算符合结合律associative law括号移动,也可写作(E32 E21)A=U。可以记作EA=U
四, 置换矩阵 Permutation
exchange rows 1 and 2 (row operation)
左乘置换矩阵可以完成原矩阵的行变换
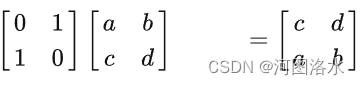
exchange columns 1 and 2 (column operation)
右乘置换矩阵则为列变换

三阶矩阵
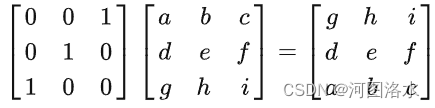
构造P 矩阵是通过对I 矩阵进行“行交换”来实现的
五, 逆矩阵 Inverse
这里主要讨论消元矩阵的逆矩阵。消元矩阵之逆矩阵的实施效果就是抵消原矩阵的消元操作。消元矩阵实现了对原矩阵A的操作,使第二行行向量[3,8,1]减掉了第一行[1,2,1]的3倍变为[0,2,-2],则逆向操作就应该是把现在的第二行行向量[0,2,-2]加上第一行[1,2,1]的3倍,从而变回原来的第二行[3,8,1]