数据结构:计算机如何存储数据的问题。DS关心的是如何高效的进行数据的读写。
算法:在特定的数据集上(不关心怎么进行具体数据的读写),如何利用数据完成特定的功能。算法本质上就是一系列运算的先后集合。
那么,如何评价一个算法的好坏?
从两种维度进行:时间效率与空间效率
时间复杂度:主要衡量一个算法的运行速度(不是实际计算机的运行速度,是理论值,在所有计算机上通用的描述)
空间复杂度:主要衡量一个算法正常执行所需要的额外空间大小,不是当前数据集本身占用的空间
所谓额外空间:为了解决这个问题,新开辟的内存大小
1. 时间复杂度
不是具体的时间,在计算机领域,其实是一个数学函数。
因为不同的计算机硬件不同,相同的算法在不同的CPU,内存这些硬件上具体的执行时间都会有差异,而且差异还挺大!
那么,利用数学函数,描述一个算法的基本操作的执行次数,就是所谓的时间复杂度。
在函数中,基本的执行语句可以不统计,基本语句和变量N毫无关系,时间复杂度看重的是执行次数和传入的变量之间的关系。
使用大O渐进表示法(数学函数,表示渐进函数)来描述一个算法的时间效率。
1.1 推导大O阶的方法:
(1)用常数1来代替函数中的所有加法常数(只要是常量,常数,都会1,无论常量有多大,用1代替)
因为常数和传入数值N变量毫无关系,此算法是一个稳定的时间效率算法,和变量无关!
(2)只保留函数的最高阶项,所有的低阶省略不计
(3)若最高阶项存在且项数不为1,统一将其最高阶的项数看做1
先看最高阶在哪,低阶全部省略;若没有变量参与,统一都是常数1。
例如:F(N)=N^2+2N+10 时间复杂度:F(N)=O(N^2)
1.2 时间复杂度评价标准
一个算法的时间复杂度存在最好、最坏、平均时间复杂度。
- 最好:任意输入的数据,最小的执行次数(算法的下界)
- 最坏:任意输入的数据,最大的执行次数(算法的上界)
- 平均:任意输入的数据,平均的执行次数
eg:在长度为N的数组中,搜索一个数据x
最坏:若x刚好在数组的末尾或者不存在该数据,则需将整个数组进行遍历,执行N次才有结果
最好:若x刚好在数组首端,执行一次就能得到结果
平均:1+2+3+......+N=(1+N)*N/2(N个数据的总共查找次数)
单个数据((1+N)*N/2)/N =N/2 时间复杂度:O(N)
衡量一个算法的时间复杂度取上界,即考虑算法的最坏情况,使用大O阶时间复杂度来描述最坏情况就是整个算法的时间复杂度。
1.3 相关例题
1. 大O阶看的是变量的最高阶,若存在多个输入变量,都需要保留各个变量的最高阶。
此时N和M都是变量,无法得知N和M谁大谁小,推导大O阶时,N和M都保留其最高阶。
时间复杂度:O(N+M)

2. N和循环次数没有关系,循环次始终为100。O(1) 和变量N无关
时间复杂度:O(1)

3. 冒泡排序
循环次数为N^2,内外层都执行N次。时间复杂度:O(N^2)

4. 二分查找
该循环每次不是从0--N,而是每次从区间的中间位置将区间一分为二,mid=N/2;
n/2+n/4+n/8+.....+n/16+....,要求这个执行次数,以2为底N的对数
时间复杂度:O(logn)
public static int binSearch(int[] arr,int value){
int left=0;
int right=arr.length-1;
while(left<=right){
int mid=(right+left)/2;
if(value<arr[mid]){
right=mid-1;
}else if(value>arr[mid])
{
left=mid+1;
}else{
return mid;
}
}
//抛出运行时异常,代表未找到元素(不能返回-1,因为-1也有可能为元素本身)
throw new NoSuchElementException("没有找到该元素!");
}(1)原则:忽略底数(换底公式:无论底数为多少,都可以换成以10为底的)
O(logn)==>忽略底数,即:对数级别的时间复杂度
如果一个算法能够做到对数级别的时间复杂度,则是非常优秀的!
(2)如何分析一个算法是对数级别的时间复杂度?
若算法是不断的将一个变量除以一个常数:N/2,或者N/3,一直除到为1或者0,则这个算法一定是对数级别的算法O(logn),也叫折纸算法。
(3)分析O(N)、O(logN)、O(N^2)随着N的不断变化,三个不同函数的变化趋势。

二分查找在一亿的有序集合中,最坏只需要29次就能查到特定元素。
5. 关于递归算法的执行时间分析
public static int fibo(int N){
return N<=2? N:fibo(N-2)+fibo(N-1);
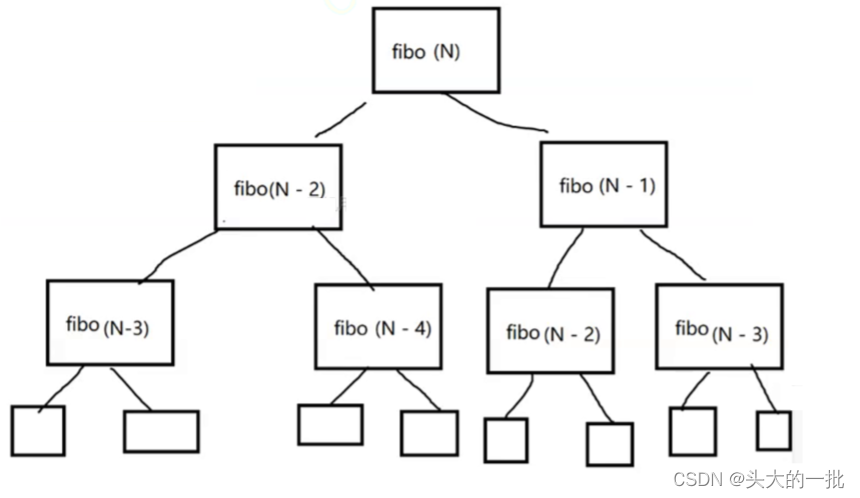
}执行次数:将fibo函数展开,执行次数就是下图中的方框个数,也就是说,求执行次数就是求结点的总个数。
2+4+6+8+....+..... 求二叉树的节点个数:2^N+1==> 时间复杂度:O(2^N)
public static int factor(int N){
//1.base case
if(N<=2){
return N;
}
return N*factor(N-1);
}执行次数:上述代码展开类比为:for(int i=1;i<N;i++){ int n*=i;},因此,时间复杂度为O(N)
总结:看一个递归算法的时间复杂度,就看递归展开,函数的执行次数即可!
2. 空间复杂度
算法执行过程中,额外开辟的空间大小。
时间复杂度描述的是算法的执行次数;
空间复杂度描述的是一个算法额外开辟的临时变量个数,也是使用大O渐进表示法。
eg:冒泡排序的空间复杂度O(1),额外开辟了一个临时变量temp。
2.1 分析空间复杂度
1. 斐波那契函数的空间复杂度
public static int[] fibo(int N){
int[] ret=new int[N+1];
ret[0]=1;
ret[1]=1;
for (int i = 2; i<=N ; i++) {
ret[i]=ret[i-1]+ret[i-2];
}
return ret;
}由于函数中出现了new int[N+1];也就是说额外开辟了一个新数组,因此空间复杂度为O(N)。
2. 递归函数的空间复杂度
对于递归函数来说,每执行一次函数,就会在系统栈上产生新的栈帧,这就属于临时空间。
public static int factor(int N){
return N<=2?N:N*factor(N-1);
}也就是说观察其展开的次数。
空间复杂度:O(N)
总结:
非递归:空间复杂度就是看函数内部new了什么
递归:看函数的展开次数,每次调用一次函数,都会额外在栈上开辟栈帧空间。
一般空间复杂度最常见的为O(1)或O(N)
在题目中,出现空间复杂度要求为O(1),代表此时不能开辟新的数组且不能使用递归。