南瓜书视频链接
以下是我的学习笔记

1、多元线性回归

首先跟着视频推了一遍，真的厉害，很清晰怎么来的


多元线性回归与一元线性回归同理利用最小二乘法求w和b。
这里我们讨论了如何使用线性模型进行回归学习，但若要做的是分类任务呢？只需要找一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来。

2、对数几率回归

虽然名字里带有回归，但是是一种分类算法。这种方法有很多优点，例如它是直接对分类可能性进行建模，无需事先假设数据分布，这样就避免了假设分布不准确所带来的问题，她不是仅预测出“类别”，而是可得到近似概率预测，这对许多需利用概率辅助决策的任务很有用；此外，对率函数是任意阶可导的凸函数，有很好的数学性质，现有的许多数值优化算法都可直接用于求取最优解。
对数几率回归算法的机器学习三要素：
1.模型：
线性模型，输出值的范围为$\left[0,1\right]$ ，近似阶跃的单调可微函数
2.策略：
极大似然估计，信息论
3.算法：
梯度下降，牛顿法

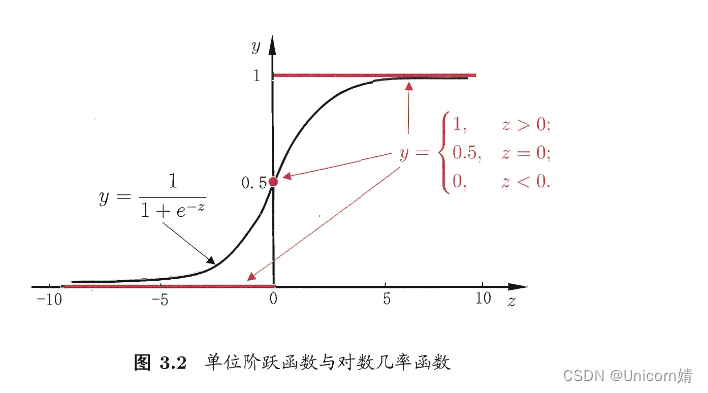
是一种“Sigmoid”函数，Sigmoid 函数这个名词是表示形式S形的函数，对数几率函数就是其中最重要的代表。这个函数相比前面的分段函数，具有非常好的数学性质，其主要优势如下：

1. 使用该函数做分类问题时，不仅可以预测出类别，还能够得到近似概率预测。这点对很多需要利用概率辅助决策的任务很有用。
2. 对数几率函数是任意阶可导函数，它有着很好的数学性质，很多数值优化算法都可以直接用于求取最优解。
   总的来说，模型的完全形式如下：
   $y=\frac{1}{1+e-\left(w^{T}x+b\right)}$

1、算法原理

在线性模型的基础上套一个映射函数来实现分类功能。

2、极大似然估计

由于损失函数通常是以最小化为优化目标，因此可以将最大化$l\left(\beta \right)$等价转化为最小化$l\left(\beta \right)$的相反数-$l\left(\beta \right)$。

3、信息论

信息论：
以概率论、随机过程为基本研究工具，研究广义通信系统的整个过程。
常见的应用有无损数据压缩（如ZIP文件）、有损数据压缩（如MP3和JPEG）等
相对熵（KL散度）：
度量两个分布的差异，其典型使用场景是用来度量理想分布和模拟分布之间的差异。

机器学习三要素中“策略”的角度来说，与理想分布最接近的模拟分布即为最优分布，因此可以通过最小化相对熵这个策略来求出最优分布。

3、二分类线性判别分析（Fisher判别）

线性判别法的思想（非常朴素）：给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近，异类样例的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别。如图：

LDA和PCA一样也常被视为一种经典的监督降维技术
LDA方法属于模式识别领域。
模式识别系统的基本构成：数据采集和预处理，特征选取，分类器设计，训练测试，计算分类结果，复杂度分析。
其中，选取特征是个技术活，如果特征过多，某些特征实际和分类结果相关性很小，就会造成过拟合，模型无法适用于新数据。不必要的特征甚至可能带来不可预知的影响。除此以外，过多的特征运算量也太大。因此，降维很必要。