目录
1.算法概述
2.仿真效果预览
3.核心MATLAB代码预览
4.完整MATLAB程序
1.算法概述
首先介绍MATLAB部分的遗传算法的优化算法介绍:
遗传算法的原理
遗传算法GA把问题的解表示成“染色体”,在算法中也即是以二进制编码的串。并且,在执行遗传算法之前,给出一群“染色体”,也即是假设解。然后,把这些假设解置于问题的“环境”中,并按适者生存的原则,从中选择出较适应环境的“染色体”进行复制,再通过交叉,变异过程产生更适应环境的新一代“染色体”群。这样,一代一代地进化,最后就会收敛到最适应环境的一个“染色体”上,它就是问题的最优解。
一、遗传算法的目的
典型的遗传算法CGA(Canonical Genetic Algorithm)通常用于解决下面这一类的静态最优化问题:考虑对于一群长度为L的二进制编码bi,i=1,2,…,n;有
bi{0,1}L (3-84)
给定目标函数f,有f(bi),并且
0
同时f(bi)≠f(bi+1)求满足下式
max{f(bi)|bi{0,1}L}
的bi。很明显,遗传算法是一种最优化方法,它通过进化和遗传机理,从给出的原始解群中,不断进化产生新的解,最后收敛到一个特定的串bi处,即求出最优解。
二、遗传算法的基本原理
长度为L的n个二进制串bi(i=1,2,…,n)组成了遗传算法的初解群,也称为初始群体。在每个串中,每个二进制位就是个体染色体的基因。根据进化术语,对群体执行的操作有三种:
1.选择(Selection)
这是从群体中选择出较适应环境的个体。这些选中的个体用于繁殖下一代。故有时也称这一操作为再生(Reproduction)。由于在选择用于繁殖下一代的个体时,是根据个体对环境的适应度而决定其繁殖量的,故而有时也称为非均匀再生(differential reproduction)。
2.交叉(Crossover)
这是在选中用于繁殖下一代的个体中,对两个不同的个体的相同位置的基因进行交换,从而产生新的个体。
3.变异(Mutation)
这是在选中的个体中,对个体中的某些基因执行异向转化。在串bi中,如果某位基因为1,产生变异时就是把它变成0;反亦反之。
遗传算法的原理可以简要给出如下:
choose an intial population
determine the fitness of each individual
perform selection
repeat
perform crossover
perform mutation
determine the fitness of each individual
perform selection
until some stopping criterion applies
这里所指的某种结束准则一般是指个体的适应度达到给定的阀值;或者个体的适应度的变化率为零。
三、遗传算法的步骤和意义
1.初始化
选择一个群体,即选择一个串或个体的集合bi,i=1,2,...n。这个初始的群体也就是问题假设解的集合。一般取n=30-160。
通常以随机方法产生串或个体的集合bi,i=1,2,...n。问题的最优解将通过这些初始假设解进化而求出。
2.选择
根据适者生存原则选择下一代的个体。在选择时,以适应度为选择原则。适应度准则体现了适者生存,不适应者淘汰的自然法则。
给出目标函数f,则f(bi)称为个体bi的适应度。以
为选中bi为下一代个体的次数。
显然.从式(3—86)可知:
(1)适应度较高的个体,繁殖下一代的数目较多。
(2)适应度较小的个体,繁殖下一代的数目较少;甚至被淘汰。
这样,就产生了对环境适应能力较强的后代。对于问题求解角度来讲,就是选择出和最优解较接近的中间解。
3.交叉
对于选中用于繁殖下一代的个体,随机地选择两个个体的相同位置,按交叉概率P。在选中的位置实行交换。这个过程反映了随机信息交换;目的在于产生新的基因组合,也即产生新的个体。交叉时,可实行单点交叉或多点交叉。
例如有个体
S1=100101
S2=010111
选择它们的左边3位进行交叉操作,则有
S1=010101
S2=100111
一般而言,交 婊显譖。取值为0.25—0.75。
4.变异
根据生物遗传中基因变异的原理,以变异概率Pm对某些个体的某些位执行变异。在变异时,对执行变异的串的对应位求反,即把1变为0,把0变为1。变异概率Pm与生物变异极小的情况一致,所以,Pm的取值较小,一般取0.01-0.2。
例如有个体S=101011。
对其的第1,4位置的基因进行变异,则有
S'=001111
单靠变异不能在求解中得到好处。但是,它能保证算法过程不会产生无法进化的单一群体。因为在所有的个体一样时,交叉是无法产生新的个体的,这时只能靠变异产生新的个体。也就是说,变异增加了全局优化的特质。
5.全局最优收敛(Convergence to the global optimum)
当最优个体的适应度达到给定的阀值,或者最优个体的适应度和群体适应度不再上升时,则算法的迭代过程收敛、算法结束。否则,用经过选择、交叉、变异所得到的新一代群体取代上一代群体,并返回到第2步即选择操作处继续循环执行。
图1中表示了遗传算法的执行过程。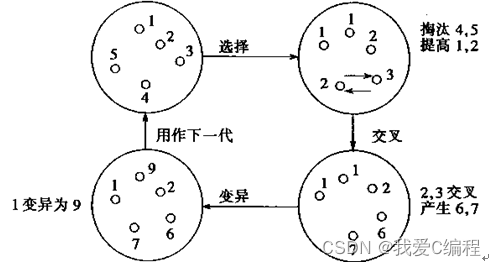
一、遗传算法的特点
1.遗传算法从问题解的中集开始嫂索,而不是从单个解开始。
这是遗传算法与传统优化算法的极大区别。传统优化算法是从单个初始值迭代求最优解的;容易误入局部最优解。遗传算法从串集开始搜索,复盖面大,利于全局择优。
2.遗传算法求解时使用特定问题的信息极少,容易形成通用算法程序。
由于遗传算法使用适应值这一信息进行搜索,并不需要问题导数等与问题直接相关的信息。遗传算法只需适应值和串编码等通用信息,故几乎可处理任何问题。
3.遗传算法有极强的容错能力
遗传算法的初始串集本身就带有大量与最优解甚远的信息;通过选择、交叉、变异操作能迅速排除与最优解相差极大的串;这是一个强烈的滤波过程;并且是一个并行滤波机制。故而,遗传算法有很高的容错能力。
4.遗传算法中的选择、交叉和变异都是随机操作,而不是确定的精确规则。
这说明遗传算法是采用随机方法进行最优解搜索,选择体现了向最优解迫近,交叉体现了最优解的产生,变异体现了全局最优解的复盖。
5.遗传算法具有隐含的并行性
遗传算法的基础理论是图式定理。它的有关内容如下:
(1)图式(Schema)概念
一个基因串用符号集{0,1,*}表示,则称为一个因式;其中*可以是0或1。例如:H=1xx 0 x x是一个图式。
(2)图式的阶和长度
图式中0和1的个数称为图式的阶,并用0(H)表示。图式中第1位数字和最后位数字间的距离称为图式的长度,并用δ(H)表示。对于图式H=1x x0x x,有0(H)=2,δ(H)=4。
(3)Holland图式定理
低阶,短长度的图式在群体遗传过程中将会按指数规律增加。当群体的大小为n时,每代处理的图式数目为0(n3)。
遗传算法这种处理能力称为隐含并行性(Implicit Parallelism)。它说明遗传算法其内在具有并行处理的特质。
简化模型:
在一个企业里,三种不一样的产品,分别定义为A, B, C,每个产品生产周期已知(表一), 需要在三个不一样容量的机器里生产,容量分别为20 30 50所产生的初始时间不一样, 而且更换不一样的机器也产生5个小时的延迟。
根据每天的订单的数量(表二, 10天订单已知, 订单会持续到达形成排列等待生产)根据交货时间和其他要求,你怎样做出决定每一个产品生产在每一个机器里.达到时间最小化? 目标函数是什么,怎样在simulink中实现。
条件:
每一个机器同时只能生产一种产品(但可以批量生产,例如同时生产几天,订单总数接近或者等于容量总数为有效)直到生产完成后才可以生产不一样的产品,但是需要产生5 小时的延迟,或者继续生产上一次的产品, 没有延迟. 同时, 每次生产完毕后,必须清洗机器, 每台机器的清洗时间分别为2, 3 ,5小时。
容量:
机器一: 20. 机器二: 30, 机器三: 50
每次生产完毕清洁时间 (小时)
机器一: 2. 机器二: 3, 机器三: 5
大概流程如下图:
三个产品10天内订单已知,每个产品生产周期已知,订单数量和交货期已知,因此怎样做出决策让订单在三个平行机器里生产达到最优化。怎样用数学建立公式, 必须满足已知条件, 然后需用GA实现优化.
让所有订单累积达到容量值,其余的推迟到下一次批次生产。 根据已知条件,然后最大容量的运行,运用偏于理解的matlab GA实现优化。。。每一步的编码都需要注释,(由于我这看不到中文,所以麻烦用文本方式标注,而且要仔细讲解结果和没优化的结果有什么不同,优化在哪里? 学习过程中,希望简化点,易理解,而且结果非常好。
2.仿真效果预览
matlab2022a仿真结果如下:

3.核心MATLAB代码预览
.................................
%%%%%%%%%%%%%%此处在Simulink等效替换%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% RandStream.setDefaultStream(RandStream('mt19937ar','seed',Seek_A));
rng(Seek_A)
A_source = floor(10*rand(1,Num))+1;
% RandStream.setDefaultStream(RandStream('mt19937ar','seed',Seek_B));
rng(Seek_B)
B_source = floor(10*rand(1,Num))+1;
% RandStream.setDefaultStream(RandStream('mt19937ar','seed',Seek_C));
rng(Seek_C)
C_source = floor(10*rand(1,Num))+1;
TASKer = [A_source',B_source',C_source'];
%生产完一批,下一批换产品导致的延迟
A_1 = Time_iniA + Time_wash(1) + Time_delay;
A_2 = Time_iniA + Time_wash(2) + Time_delay;
A_3 = Time_iniA + Time_wash(3) + Time_delay;
A_delays_diff = [A_1,A_2,A_3];
B_1 = Time_iniB + Time_wash(1) + Time_delay;
B_2 = Time_iniB + Time_wash(2) + Time_delay;
B_3 = Time_iniB + Time_wash(3) + Time_delay;
B_delays_diff = [B_1,B_2,B_3];
C_1 = Time_iniC + Time_wash(1) + Time_delay;
C_2 = Time_iniC + Time_wash(2) + Time_delay;
C_3 = Time_iniC + Time_wash(3) + Time_delay;
C_delays_diff = [C_1,C_2,C_3];
%生产完一批,下一批还是生产同样的产品(根据修改后的要求可知,只要是同一批产品,则可以连续生产)
A_1 = 0;
A_2 = 0;
A_3 = 0;
A_delays_same = [A_1,A_2,A_3];
B_1 = 0;
B_2 = 0;
B_3 = 0;
B_delays_same = [B_1,B_2,B_3];
C_1 = 0;
C_2 = 0;
C_3 = 0;
C_delays_same = [C_1,C_2,C_3];
for i = 1:Num
Machine_sel{i,1} = [1,1,1];
Machine_sel{i,2} = [2,2,2];
Machine_sel{i,3} = [3,3,3];
end
%根据每个机器的容量,来等效出每个单个订单的生产时间,但在后面计算过程中,当期满足判决条件的时候,时间则为72,96或者120
for i = 1:Num
Machine_time{i,1} = [A_source(i)/Cap(1)*ProduceA,B_source(i)/Cap(1)*ProduceB,C_source(i)/Cap(1)*ProduceC];
Machine_time{i,2} = [A_source(i)/Cap(2)*ProduceA,B_source(i)/Cap(2)*ProduceB,C_source(i)/Cap(2)*ProduceC];
Machine_time{i,3} = [A_source(i)/Cap(3)*ProduceA,B_source(i)/Cap(3)*ProduceB,C_source(i)/Cap(3)*ProduceC];
end
%一下是遗传算法的一些参数
%个体
Num_gene = 20;
%遗传次数
Iteration = 400;
%代沟
DG = 0.9;
%交叉率
cross_rate= 0.8;
%变异率
by_rate = 0.6;
%计数器
Cnter = 0;
[Nums_time,Num_ABC] = size(Machine_sel);
Best_save = zeros(2, Iteration);
All_Number = Nums_time*Num_ABC;
Number = zeros(1,Nums_time);
for i=1:Nums_time
Number(i)=Num_ABC;
end
Random_save_machine = zeros(Num_gene,2*All_Number);
for j=1:Num_gene
Number2=Number;
for i=1:All_Number
%产品编号ABC - > 123
val = unidrnd(Nums_time);
while Number2(val)==0
val = unidrnd(Nums_time);
end
%产品编号
Random_save_machine(j,i) = val;
Number2(val) = Number2(val)-1;
%机器编号
Temp = Machine_sel{val,Num_ABC-Number2(val)};
SizeTemp = length(Temp);
%随机产品机器
Random_save_machine(j,i+All_Number) = unidrnd(SizeTemp);
end
end
%定义fitness
[Value_Product,ObjV,Product,Genes] = func_fitness(Random_save_machine,Num_machine,Machine_time,Machine_sel);
s = RandStream('mt19937ar','Seed',0);
RandStream.setGlobalStream(s);
%开始优化迭代
while Cnter <= Iteration
Cnter
isover = 0;
%适应度值
Value_fit = ranking(ObjV);
%选择
GA_Oper = select('rws', Random_save_machine, Value_fit, DG);
%交叉
GA_Oper = func_Gene_cross(GA_Oper,cross_rate,Machine_sel,Machine_time);
%变异
GA_Oper = func_aberrance(GA_Oper,by_rate,Machine_sel,Machine_time);
%适应度值
[Value_Product,Obj_Product,Product,Genes,TYPE] = func_fitness(GA_Oper,Num_machine,Machine_time,Machine_sel);
%新种群
[Random_save_machine,ObjV] = reins(Random_save_machine, GA_Oper,1, 1, ObjV, Obj_Product);
Cnter = Cnter + 1;
%保存最值
Best_save(1,Cnter) = min(ObjV);
Best_save(2,Cnter) = mean(ObjV);
%记录最佳值
if Cnter == 1
Values1 = Value_Product;
Values2 = Product;
MinVal = min(ObjV);
STemp = Genes;
end
if MinVal > Best_save(1,Cnter)
Values1 = Value_Product;
Values2 = Product;
MinVal = Best_save(1,Cnter);
STemp = Genes;
end
%延期判决
if isover == 1
Cnter = Cnter-1;%重新开始本次迭代
else
Cnter =Cnter;
end
Best_V(Cnter)=min(ObjV);
Best_M(Cnter) = mean(ObjV)
end
%当前最佳值
Value_Product = Values1;
Product = Values2;
Genes = STemp;
%描绘解的变化
02_015m4.完整MATLAB程序
matlab源码说明_我爱C编程的博客-CSDN博客
V