2485. 找出中枢整数
给你一个正整数 n ,找出满足下述条件的 中枢整数 x :
1和x之间的所有元素之和等于x和n之间所有元素之和。
返回中枢整数 x 。如果不存在中枢整数,则返回 -1 。题目保证对于给定的输入,至多存在一个中枢整数。
提示
1 <= n <= 1000
示例
输入:n = 8
输出:6
解释:6 是中枢整数,因为 1 + 2 + 3 + 4 + 5 + 6 = 6 + 7 + 8 = 21 。
思路
由于数据范围很小,暴力模拟即可。
class Solution {
public:
int pivotInteger(int n) {
int tot = (1 + n) * n / 2, sum = 0;
for (int i = 1; i <= n; i++) {
sum += i;
if (sum == tot - sum + i) return i;
}
return -1;
}
};
2486. 追加字符以获得子序列
给你两个仅由小写英文字母组成的字符串 s 和 t 。
现在需要通过向 s 末尾追加字符的方式使 t 变成 s 的一个 子序列 ,返回需要追加的最少字符数。
子序列是一个可以由其他字符串删除部分(或不删除)字符但不改变剩下字符顺序得到的字符串。
提示
1 <= s.length, t.length <= 10^5s和t仅由小写英文字母组成
示例
输入:s = "coaching", t = "coding"
输出:4
解释:向 s 末尾追加字符串 "ding" ,s = "coachingding" 。
现在,t 是 s ("coachingding") 的一个子序列。
可以证明向 s 末尾追加任何 3 个字符都无法使 t 成为 s 的一个子序列。
思路
双指针,看下t中最多有多少个字符可以在s中得到。
class Solution {
public:
int appendCharacters(string s, string t) {
int n = s.size(), m = t.size();
int i = 0, j = 0;
while (i < n && j < m) {
if (s[i] == t[j]) j++;
i++;
}
return m - j; // 还差多少个
}
};
2487. 从链表移除节点
给你一个链表的头节点 head 。
对于列表中的每个节点 node ,如果其右侧存在一个具有 严格更大 值的节点,则移除 node 。
返回修改后链表的头节点 head 。
提示
- 给定列表中的节点数目在范围
[1, 10^5]内 1 <= Node.val <= 10^5
示例
输入:head = [5,2,13,3,8]
输出:[13,8]
解释:需要移除的节点是 5 ,2 和 3 。
- 节点 13 在节点 5 右侧。
- 节点 13 在节点 2 右侧。
- 节点 8 在节点 3 右侧。
思路
单调栈,维护一个单调递减的栈即可。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeNodes(ListNode* head) {
ListNode* hh = new ListNode(1e5 + 5, head);
stack<ListNode*> stk;
stk.push(hh);
for (ListNode* cur = head; cur != nullptr; cur = cur->next) {
while (!stk.empty() && stk.top()->val < cur->val) stk.pop();
// 中间部分的节点全部要被移除, 只需要连接第一个大于cur的节点即可
stk.top()->next = cur;
stk.push(cur);
}
return hh->next;
}
};
另:递归做法
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeNodes(ListNode* head) {
if (head->next == nullptr) return head;
ListNode* x = removeNodes(head->next);
return head->val >= x->val ? new ListNode(head->val, x) : x;
}
};
2488. 统计中位数为K的子数组
给你一个长度为 n 的数组 nums ,该数组由从 1 到 n 的 不同 整数组成。另给你一个正整数 k 。
统计并返回 num 中的 中位数 等于 k 的非空子数组的数目。
注意:
- 数组的中位数是按 递增 顺序排列后位于 中间 的那个元素,如果数组长度为偶数,则中位数是位于中间靠 左 的那个元素。
- 例如,
[2,3,1,4]的中位数是2,[8,4,3,5,1]的中位数是4。
- 例如,
- 子数组是数组中的一个连续部分。
提示:
n == nums.length1 <= n <= 10^51 <= nums[i], k <= nnums中的整数互不相同
示例:
输入:nums = [3,2,1,4,5], k = 4
输出:3
解释:中位数等于 4 的子数组有:[4]、[4,5] 和 [1,4,5] 。
思路
首先找到k的下标,假设为x,我们需要找到所有的[i, j],其中i在x左侧,j在x右侧。设区间[i, x]内小于k的元素个数为leftLessCnt,大于k的元素个数为leftGreatCnt;同理设区间[x, j]中小于k的元素个数为rightLessCnt,大于k的元素个数为rightGreatCnt。由于k是中位数,那么需要满足[i, j]整个区间内,小于k的元素个数,与大于k的元素个数,相等,或者左侧比右侧少1。
那么我们需要找出所有的[i, j],使其满足
leftLessCnt + rightLessCnt = leftGreatCnt + rightGreatCnt或者
leftLessCnt + rightLessCnt = leftGreatCnt + rightGreatCnt - 1
我周赛当天的想法是对于左右两侧,分别维护一下小于k的元素个数与大于k的元素个数的差值。下面是我周赛当天的代码。
const int N = 1e5 + 10;
class Solution {
public:
vector<vector<int>> rFreq;
int countSubarrays(vector<int>& nums, int k) {
int pos = 0, n = nums.size();
for (int i = 0; i < n; i++) {
if (nums[i] == k) {
pos = i;
break;
}
}
// printf("pos = %d\n", pos);
// f[i][0] 表示 lCnt < gCnt, 相差i
// f[i][1] 表示 lCnt > gCnt, 相差i
rFreq = vector<vector<int>>(n + 1, vector<int>(2, 0));
// 求一下右侧的cnt
int lCnt = 0, gCnt = 0;
for (int i = pos + 1; i < n; i++) {
if (nums[i] < k) lCnt++;
else gCnt++;
if (lCnt == gCnt) rFreq[0][0]++, rFreq[0][1]++;
else if (lCnt < gCnt) rFreq[gCnt - lCnt][0]++;
else rFreq[lCnt - gCnt][1]++;
}
rFreq[0][0]++;
rFreq[0][1]++;
// for (int i = 0; i <= n; i++) {
// if (rFreq[i][0]) printf("freq[%d][0] = %d\n", rFreq[i][0]);
// if (rFreq[i][1]) printf("freq[%d][1] = %d\n", rFreq[i][1]);
// }
int ans = 0; // 长度为1的
// 计算左侧
lCnt = gCnt = 0;
for (int i = pos; i >= 0; i--) {
if (nums[i] < k) lCnt++;
else if (nums[i] > k) gCnt++;
// printf("i = %d, lCnt = %d, gCnt = %d\n", i, lCnt, gCnt);
int d = gCnt - lCnt;
if (d == 0) {
// printf("d = %d, [0][0] = %d, [1][0] = %d\n", d, rFreq[0][0], rFreq[1][0]);
ans += rFreq[0][0] + rFreq[1][0]; // g > l
}
else if (d < 0) {
// printf("d = %d, [-d][0] = %d, [-d+1][0] = %d\n", d, rFreq[-d][0], rFreq[-d+1][0]);
ans += rFreq[-d][0] + rFreq[-d + 1][0];
}
else {
// printf("d = %d, [d][1] = %d, [d - 1][1] = %d\n", d, rFreq[d][1], rFreq[d - 1][1]);
ans += rFreq[d][1] + rFreq[d - 1][1];
}
// printf("ans = %d\n", ans);
}
return ans;
}
};
很遗憾,当时边界问题没处理好,直到12点04分才调试通过,然而12点比赛就结束了,痛失AK机会。并且我代码写的可谓又臭又长,十分难看。下面是今天(2022/12/20)重写的代码。
class Solution {
public:
int countSubarrays(vector<int>& nums, int k) {
int n = nums.size(), x = n;
unordered_map<int, int> freq;
int lCnt = 0, gCnt = 0; // 小于k和大于k的元素个数
for (int i = 0; i < n; i++) {
if (nums[i] == k) x = i;
// 一次遍历同时找出坐标x, 并处理右侧的情况
if (i >= x) {
if (nums[i] < k) lCnt++;
if (nums[i] > k) gCnt++;
freq[gCnt - lCnt]++;
}
}
// 处理左边
int ans = 0;
lCnt = gCnt = 0;
for (int i = x; i >= 0; i--) {
if (nums[i] < k) lCnt++;
if (nums[i] > k) gCnt++;
ans += freq[lCnt - gCnt] + freq[lCnt - gCnt + 1];
}
return ans;
}
};
再提供一个版本,这个版本是今天重做时,没有回看之前代码的情况下,自己重新写的。相对而言更多是推公式。
设l[i]表示区间[i, x]内小于k的元素数量,那么很明显的,[i, x]内大于k的元素数量应该是x - i - l[i]
同理设r[j]表示区间[x, j]内小于k的元素数量,那么,[x, j]内大于k的元素数量是j - x - r[j]
我们需要找到所有的[i, j]对,使得其满足
l[i] + r[j] = x - i - l[i] + j - x - r[j] 或
l[i] + r[j] = x - i - l[i] + j - x - r[j] - 1
整理一下,将i相关的项全部移到一边,j相关的项全部移到另一边,整理一下有
2 * l[i] + i = j - 2 * r[j] 或
2 * l[i] + i = j - 2 * r[j] - 1
那么我们可以处理x右侧的所有位置j,计算出j - 2 * r[j],并计数。
然后遍历x左侧的所有位置,对于每个i,找到与之匹配的所有j即可。
class Solution {
public:
int countSubarrays(vector<int>& nums, int k) {
int n = nums.size();
vector<int> l(n), r(n);
// 先找到k这个数的所在位置
int x = 0;
for (int i = 0; i < n; i++) {
if (nums[i] == k) {
x = i;
break;
}
}
// 预处理l
int cnt = 0;
for (int i = x; i >= 0; i--) {
if (nums[i] < k) cnt++;
l[i] = cnt;
}
unordered_map<int, int> m;
// 预处理r
cnt = 0;
for (int i = x; i < n; i++) {
if (nums[i] < k) cnt++;
r[i] = cnt;
int u = i - 2 * r[i];
m[u]++; // 计数+1
}
int ans = 0;
for (int i = 0; i <= x; i++) {
int u = 2 * l[i] + i;
ans += m[u] + m[u + 1];
}
return ans;
}
};
同样的,可以对代码进行一下优化。
class Solution {
public:
int countSubarrays(vector<int>& nums, int k) {
// 先找到k这个数的所在位置
int n = nums.size(), x = n, cnt = 0, ans = 0;
unordered_map<int, int> freq;
for (int i = 0; i < n; i++) {
if (nums[i] == k) x = i;
if (i >= x) {
if (nums[i] < k) cnt++;
freq[i - 2 * cnt]++;
}
}
cnt = 0;
for (int i = x; i >= 0; i--) {
if (nums[i] < k) cnt++;
int u = 2 * cnt + i;
ans += freq[u] + freq[u + 1];
}
return ans;
}
};
总结
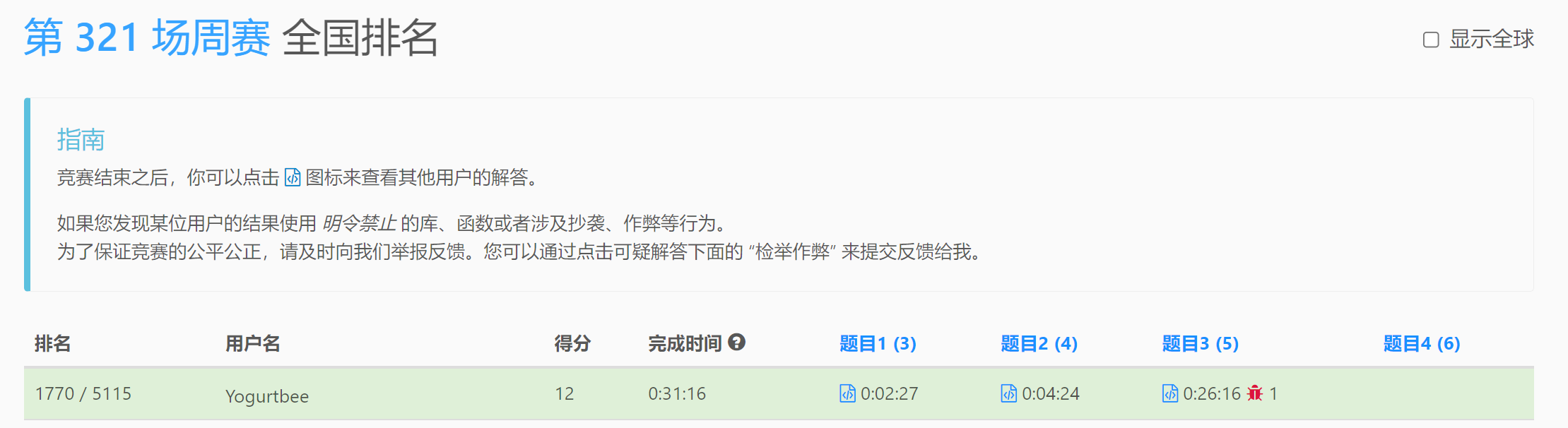
这次的T4难度不大,有机会AK的,但很可惜。
T1简单模拟;T2双指针模拟;T3栈;T4哈希表。





![[ vulhub漏洞复现篇 ] Airflow dag中的命令注入漏洞复现 CVE-2020-11978](https://img-blog.csdnimg.cn/2828b8c19a5a409d9c1ad89b01375844.png)