【吴恩达老师《机器学习》】课后习题5之【偏差与方差】

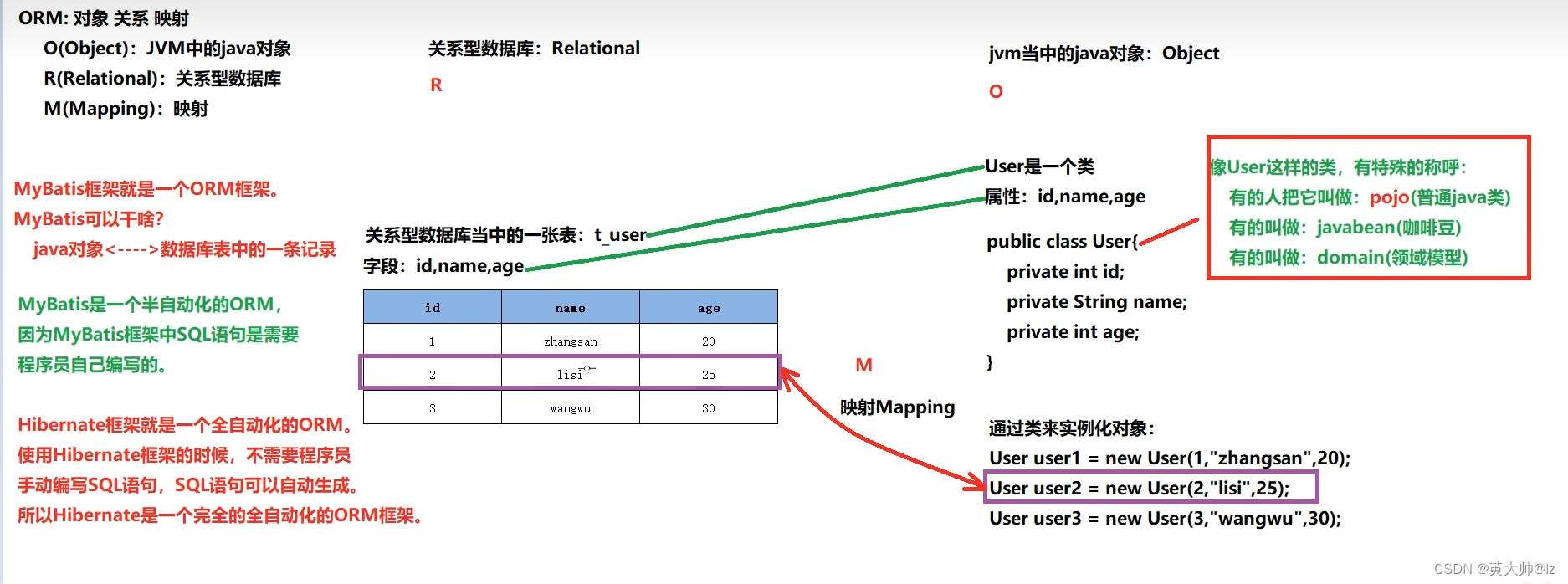
在本练习中，您将实现正则化线性回归，并使用它来研究具有不同偏差-方差特性的模型。

在练习的前半部分，您将实现正则化线性回归，利用水库水位的变化来预测从大坝流出的水量。
在后半部分中，您将对调试学习算法进行一些诊断，并检查偏差和偏差的影响。
这次练习将会了解如何改进机器学习算法，包括过拟合、欠拟合的状态判断以及学习曲线的绘制。

一些概念

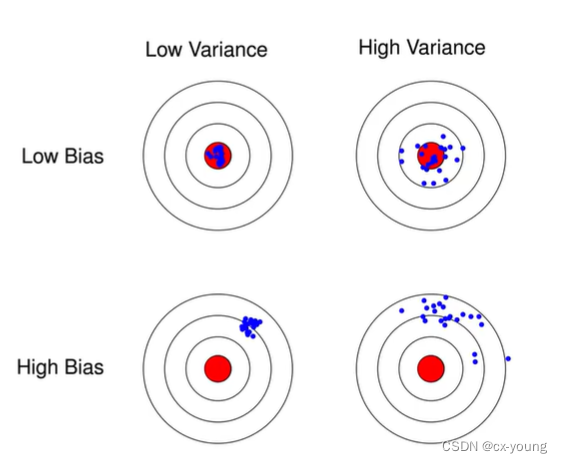
偏差Bias：
预测值与真实值的差距，表示算法本身的拟合能力
方差Variance：
预测值的变化范围，表示数据扰动所造成的影响
如图所示（图片来自网络偏差与方差）
训练集：训练模型，类似课后练习小题
验证集：模型选择，模型的最终优化，类似于模拟卷
测试集：利用训练好的模型测试其泛化能力，类似于高考验证
之前的练习中，仅用到了训练集，实际开发者，一般使用训练集进行模型训练出几个模型，验证集验证哪个模型最优并进行优化，再使用测试集进行验证模型的泛化能力
损失函数和梯度见下图

案例

案例描述与数据集

案例：利用水库水位变化预测大坝出水量
数据集：ex5data1.mat【吴恩达老师】机器学习、深度学习课后习题所有的数据集】
在本练习中，您将实现正则化线性回归，并使用它来研究具有不同偏差-方差特性的模型。
在练习的前半部分，您将实现正则化线性回归，利用水库水位的变化来预测从大坝流出的水量。
在后半部分中，您将对调试学习算法进行一些诊断，并检查偏差和偏差的影响。

1.导包

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
from scipy.optimize import minimize

2.读取数据

# 导入数据集
data = loadmat('ex5data1.mat')

# 打印data字典里的键  1. X和y训练集数据  2. Xtest和ytest是测试集数据  3.Xval和yval是验证集数据
print('打印data字典里的键：', data.keys())# 打印data字典里的键： dict_keys(['__header__', '__version__', '__globals__', 'X', 'y', 'Xtest', 'ytest', 'Xval', 'yval'])

# 训练集
X_train, y_train = data['X'], data['y']
print('打印训练集维度：', X_train.shape, y_train.shape)  # (12, 1) (12, 1) 表明有12个样本，1个特征

# 验证集
X_val, y_val = data['Xval'], data['yval']
print('打印验证集维度：', X_val.shape, y_val.shape)  # (21, 1) (21, 1)表明有21个样本，1个特征

# 测试集
X_test, y_test = data['Xtest'], data['ytest']
print('打印测试集维度：', X_test.shape, y_test.shape)  # (21, 1) (21, 1) 表明有21个样本，1个特征

3.对训练集、验证集、测试集数据进行处理

# 添加偏置项：每行的开头插入一个值为1的列
X_train = np.insert(X_train, 0, 1, axis=1)
X_val = np.insert(y_val, 0, 1, axis=1)
X_test = np.insert(X_test, 0, 1, axis=1)

4.数据可视化

4.1先进行线性回归，看一下效果

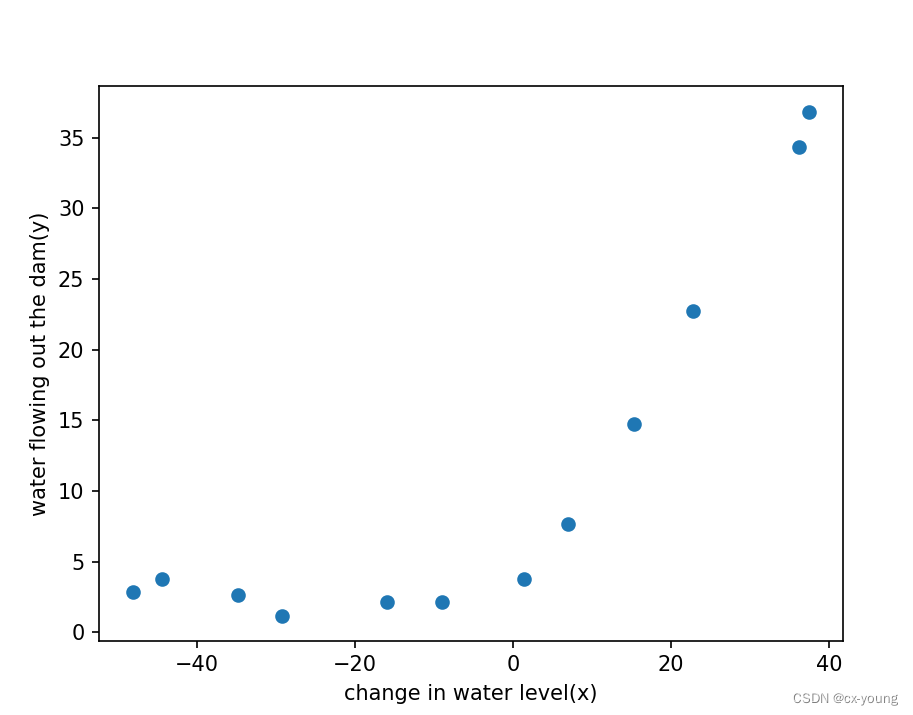
4.1.1绘制散点图查看数据

'''绘制散点图的函数 plot_data()。
它使用训练数据集的特征和标签来创建一个散点图，以可视化特征与标签之间的关系。'''


def plot_data():
    fig, ax = plt.subplots()  # 创建图形对象(fig)和一个坐标轴对象(ax)
    # 使用scatter函数绘制散点图，      X_train[:, 1]表示   使用训练数据集中第二列特征作为X轴坐标  水位的变化
    #                              y_train表示        使用训练数据集中的标签作为Y轴坐标      出水量
    # 按照每个样本的特征和标签的取值，在散点图显示它们之间的关系
    ax.scatter(X_train[:, 1], y_train)
    ax.set(xlabel='change in water level(x)',
           ylabel='water flowing out the dam(y)')


# 调用plot_data函数,看原始数据分布散点图
plot_data()
# 显示图形
plt.show()

运行结果：
在这里插入图片描述

4.1.2构造损失函数（带正则化）和梯度

在这里插入图片描述

# 损失函数
def reg_cost(theta, X, y, lamda):
    cost = np.sum(np.power((X @ theta - y.flatten()), 2))
    reg = theta[1:] @ theta[1:] * lamda  # 第一项不参与正则化
    return (cost + reg) / (2 * len(X))


# 测试 损失函数
# X_train.shape[1]表示训练数据集X_train的列数，也就是特征的个数。
# 然后，使用np.ones()函数创建了一个元素均为1的数组，并赋值给theta变量
# 模型参数初始化或迭代优化过程中的初始点。
theta = np.ones(X_train.shape[1])
lamda = 1
result_cost = reg_cost(theta, X_train, y_train, lamda)

print(result_cost)  # 303.9931922202643

# 梯度
def reg_gradient(theta, X, y, lamda):
    grad = (X @ theta - y.flatten()) @ X
    reg = lamda * theta
    reg[0] = 0  # 不改变维度，直接赋值为0第一行不参与运算
    return (grad + reg) / (len(X))


# 测试梯度
result_gradient = reg_gradient(theta, X_train, y_train, lamda)
print(result_gradient)  # [-15.30301567 598.25074417]

4.1.3绘制线性模型

# 这个训练过程可以用来训练各种不同的机器学习模型，如线性回归、逻辑回归等
'''参数特征矩阵 X、目标变量 y 和正则化参数 lambda 作为输入，并返回通过最小化代价函数得到的模型参数 theta
theta = np.ones(X.shape[1]): 初始化模型参数theta，将其设置为全1数组，X.shape[1]表示 X列数 即特征的数量
res = minimize...:使用优化算法minimize()最小化损失函数fun，并得到最优的模型参数'''


def train_model(X, y, lamda):
    theta = np.ones(X.shape[1])
    res = minimize(fun=reg_cost,  # 损失函数
                   x0=theta,  # 初始参数值
                   args=(X, y, lamda),  # 附加参数
                   method='TNC',  # 使用TNC算法进行优化
                   jac=reg_gradient)  # 表示损失函数的梯度函数
    return res.x  # 返回通过优化算法得到的最优模型参数theta


# lamda目前不使用，因为是线性模型不会过拟合
theta_final = train_model(X_train, y_train, lamda=0)

# 使用线性回归拟合数据
# 调用plot_data函数
plot_data()
# x轴只取第2列
plt.plot(X_train[:, 1], X_train @ theta_final, c='r')
plt.show()  # 查看会发现，偏差非常大，处于欠拟合的状态

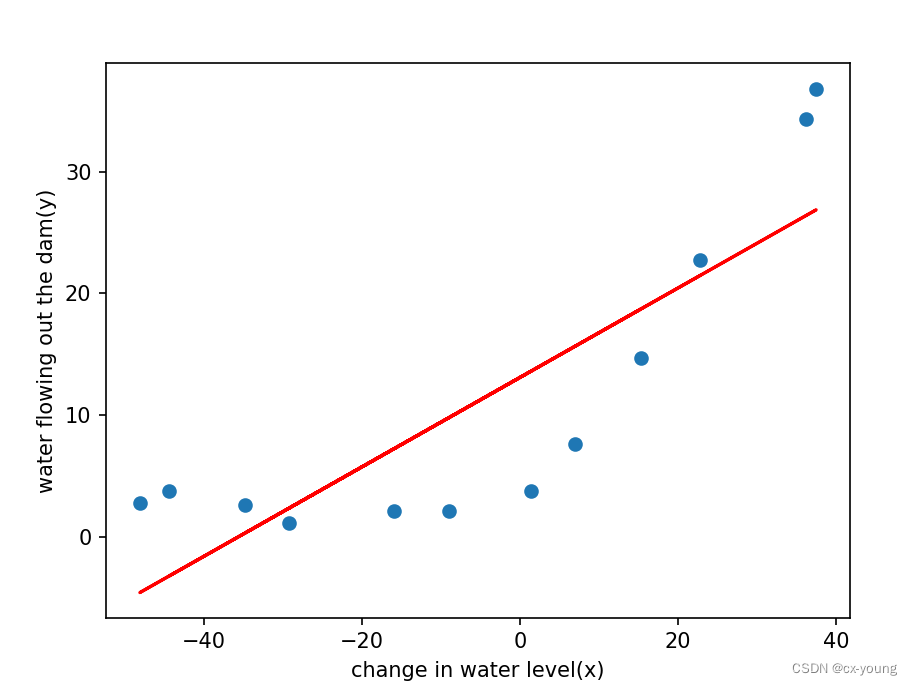
在这里插入图片描述

5.绘制样本个数VS误差

# 任务：训练样本从1开始递增进行训练，比较训练集和验证集上的损失函数的变化情况，观察一下误差的变化情况
# 定义一个函数展现整个学习过程，即随着样本数量的增加，巡礼那几成本和验证集成本的学习误差的曲线
def plot_learning_curve(X_train, y_train, X_val, y_val, lamda):
    # 使用列表x存放训练样本的个数
    x = range(1, len(X_train) + 1)
    # 再定义两个空列表分别存放：验证集和训练集损失函数
    training_cost = []
    cv_cost = []
    # 遍历x中的每个元素，表述不断增加训练样本的数量来计算学习曲线
    for i in x:
        # 调用train_model()函数，输入前i个训练样本和相应的目标值，以及正则化参数lamda，返回模型的参数结果res
        # X_train[:i, :]将返回训练数据集中的前 i 行的所有列
        res = train_model(X_train[:i, :], y_train[:i, :], lamda)
        # 调用reg_cost()函数，计算使用前i个训练样本拟合得到的模型在训练集上的损失函数值
        train_cost_i = reg_cost(res, X_train[:i, :], y_train[:i, :], lamda)
        # 调用reg_cost()函数，计算使用前i个训练样本拟合得到的模型在验证集上的损失函数值
        cv_cost_i = reg_cost(res, X_val, y_val, lamda)
        # 将训练集和验证集的损失函数值分别添加到两个列表中
        training_cost.append(train_cost_i)
        cv_cost.append(cv_cost_i)
    # 横轴为训练样本的数量 x，纵轴为对应的训练集和验证集的损失函数值。
    plt.plot(x, training_cost, label='training cost')
    plt.plot(x, cv_cost, label='cv cost')
    # 显示图例，标明不同曲线的含义
    plt.legend()
    # 设置横轴和纵轴的标签
    plt.xlabel('number of training examples')
    plt.ylabel('error')
    # 显示绘制的学习曲线图
    plt.show()


# 传入相应的训练集、验证集以及正则化参数，可以绘制出学习曲线来评估模型的性能和训练集大小对模型的影响
plot_learning_curve(X_train, y_train, X_val, y_val, lamda=0)

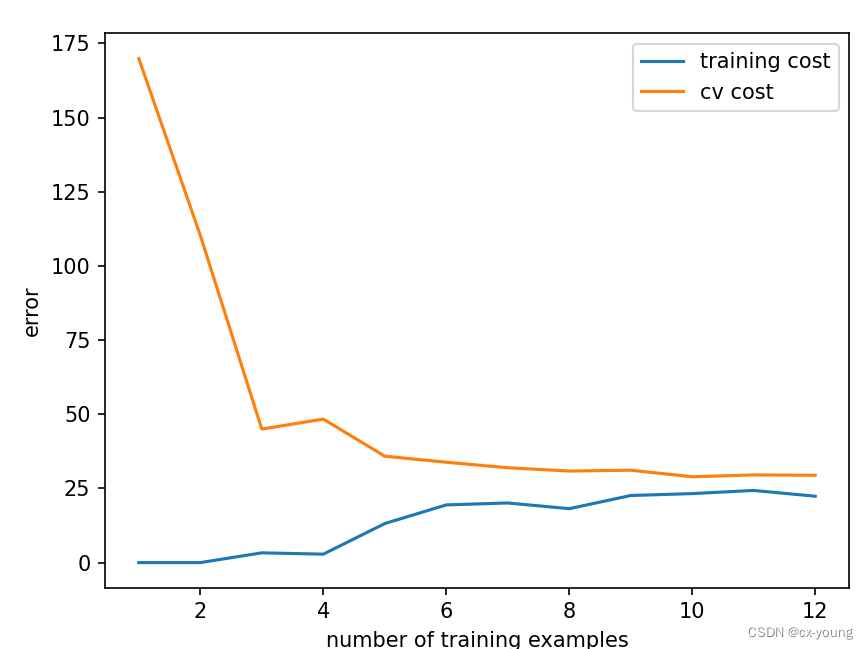
在这里插入图片描述
由图可知，随着样本数量的增加，训练集成本的误差逐渐上升，而验证集成本误差逐渐下降。最终，训练集和验证集的误差都比较大，属于高偏差，即模型是欠拟合的，那么如何改进呢？

6.多项式特征、归一化

已经知道简单的线性模型造成了欠拟合，那么如何解决呢？
我们可以计算Jtrain(θ)和Jcv(θ)

如果两者同时很大，则是存在高偏差问题，欠拟合
如果Jcv(θ)比Jtrain(θ)大很多，则存在高方差问题，过拟合

高方差的解决方案
1.采集更多样本数据
2.减少特征数量，去除非主要的特征
3.增加正则化参数λ
高偏差的解决方案
1.引入更多的相关特征
2.采用多项式特征
3.减小正则化参数λ

为解决高偏差问题，由于我们未使用λ，也只有水位一个特征，所以还剩下第2个解决方案，即采取多项式特征
在这里插入图片描述

# 任务：构造多项式特征（将原本只有一列的特征x通过生成高阶次项创造多个特征），进行多项式回归
'''多项式特征生成函数
X：传入特征矩阵X和多项式阶数power
用于生成具有不同阶数多项式特征的新特征矩阵，帮助模型更好拟合非线性关系'''


def poly_feature(X, power):
    for i in range(2, power + 1):  # 循环从2到给定的多项式阶数power+1
        # 在输入特征矩阵X 的最后一列插入一列
        # 首先使用 np.power() 函数计算原始特征矩阵 X 的第二列（索引为 1）的 i 次方。X[:, 1] 表示取出矩阵 X 的所有行的第二列。
        # 然后，使用 np.insert() 函数将得到的新特征插入到矩阵 X 的最后一列。具体而言，X.shape[1] 返回 X 的列数，即特征的数量，axis=1 表示按列方向插入数据。
        # 通过这样的操作，我们将生成新的特征矩阵 X，其中包含了原始特征的不同次幂的组合。
        X = np.insert(X, X.shape[1], np.power(X[:, 1], i), axis=1)
    return X

'''计算特征矩阵 X 的每个特征的均值和方差
这些统计信息在数据处理中经常被用来进行特征缩放、归一化等操作，以提高模型训练的效果
计算均值和方差时应使用训练集的统计信息'''


def get_means_stds(X):
    # 使用 np.mean() 函数计算特征矩阵 X 沿着轴 0（列）的均值。
    # 这意味着函数将对特征矩阵 X 的每列进行均值和标准差的计算，也就是计算每个特征的均值和标准差。
    # 返回一个包含每个特征的均值的数组 means
    means = np.mean(X, axis=0)
    # 方差
    stds = np.std(X, axis=0)
    return means, stds


'''
特征归一化函数，接收特征矩阵X，均值数组means、方差数组stds作为输入
并返回归一化后的特征矩阵X
注：特征归一化是一种常见的数据预处理操作，可以提高模型训练效果，并确保不同特征之间的尺度差异不会对模型产生不良影响
通常情况下，归一化处理使用训练集进行'''


def feature_normalize(X, means, stds):
    # 第一列假设为常数项或类别信息，不需要进行归一化操作
    X[:, 1:] = (X[:, 1:] - means[1:]) / stds[1:]
    return X


# 测试
power = 6
# 对训练集、验证集、测试集分别调用 多项式特征生成函数
X_train_poly = poly_feature(X_train, power)
X_val_poly = poly_feature(X_val, power)
X_test_poly = poly_feature(X_test, power)
# 获取训练集的均值和方差
train_means, train_stds = get_means_stds(X_train_poly)
# 对训练集、验证集、测试集进行归一化处理
X_train_norm = feature_normalize(X_train_poly, train_means, train_stds)
X_val_norm = feature_normalize(X_val_poly, train_means, train_stds)
X_test_norm = feature_normalize(X_test_poly, train_means, train_stds)
# 获取最优的theta参数
theta_fit = train_model(X_train_norm, y_train, lamda=0)

'''绘制多项式拟合曲线的函数 plot_poly_fit()。
首先调用了之前定义的 plot_data() 函数，将训练数据集的散点图显示在图形界面中。然后使用训练得到的最优模型参数 theta_fit，在图形界面中绘制多项式拟合曲线'''


def plot_poly_fit():
    # 调用其可以在图形界面中显示训练集的散点图，帮助我们观察特征和标签之间的关系
    # 对于理解数据集、探索数据、以及选择适当的模型都非常有帮助
    plot_data()

    x = np.linspace(-60, 60, 100)  # 生成一个包含100个等间距数值的数组，范围从-60到60。这个数组将作为 X 轴的取值范围
    xx = x.reshape(100, 1)  # 将数组 x 进行形状变换，改为一个100行1列的二维数组。这样做是为了满足多项式特征的输入格式要求
    xx = np.insert(xx, 0, 1, axis=1)  # 在数组 xx 的第一列插入全1的列向量。这是为了与之前的训练数据集保持一致，添加了一个截距项
    xx = poly_feature(xx, power)  # 将原始特征矩阵 xx 转化为多项式特征矩阵。这样可以根据多项式的阶数 power 扩展特征
    xx = feature_normalize(xx, train_means,
                           train_stds)  # 对多项式特征矩阵 xx 进行归一化处理。这里使用训练数据集的均值 train_means和方差train_stds 进行归一化，保证与之前的训练数据集保持一致
    plt.plot(x, xx @ theta_fit,
             'r--')  # 绘制多项式拟合曲线，x为 X 轴，xx @ theta_fit 表示通过最优模型参数 theta_fit 对多项式特征矩阵 xx 进行预测得到的 Y 轴坐标。'r--' 表示以红色虚线的形式进行绘制
    plt.show()


# 通过调用 plot_poly_fit() 函数，可以在图形界面中显示训练数据集的散点图，并绘制多项式拟合曲线。这有助于直观地观察拟合效果，并评估模型的性能。
plot_poly_fit()

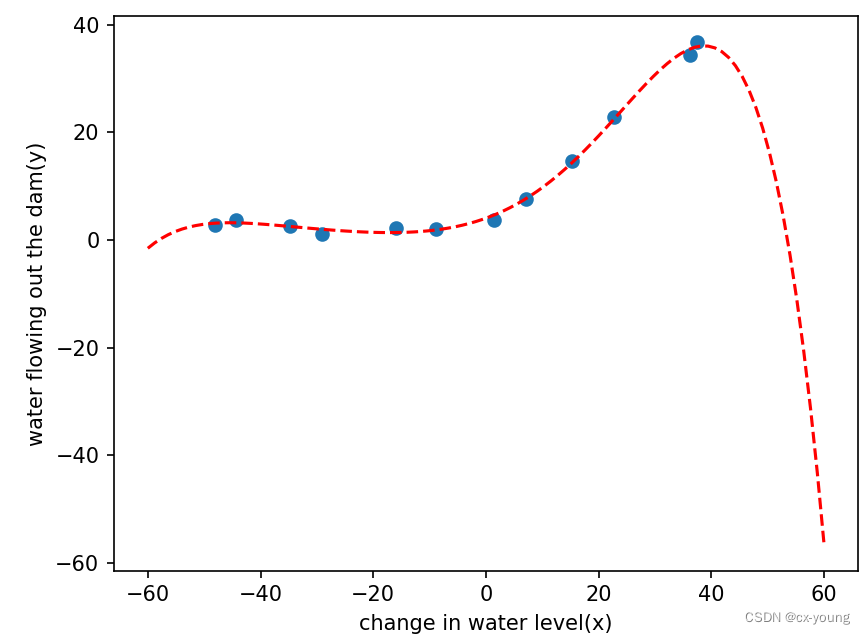
在这里插入图片描述

7.lamda正则化参数的选取对模型的影响

7.1不使用lamda，将其设置为0

# 正则化影响 lamda设为0，因为正则化只在训练时才有
# 通过绘制学习曲线的误差函数，来看出它在训练集和验证集上表现为过拟合
plot_learning_curve(X_train_norm, y_train, X_val_norm, y_val, lamda=0)  # 高方差，过拟合

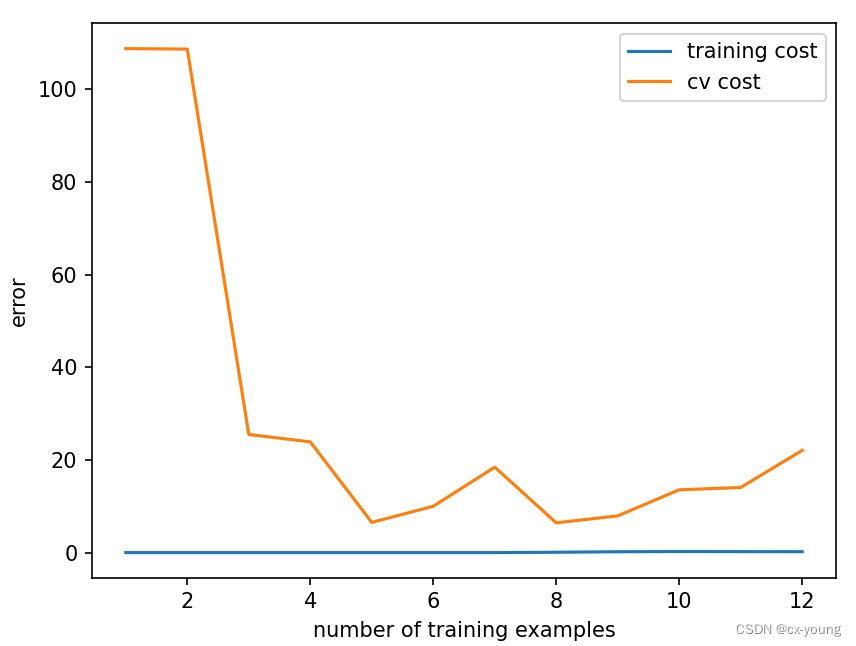
在这里插入图片描述
由上图可以看出训练集的误差几乎为0，而验证集的误差还比较高，这表示目前模型状态为高方差，表现为过拟合。

7.2将lamda设置为1

使用正则化是解决过拟合的好办法。通过使用lamda,将它从0变成1，即为开启正则化。

# 使用正则化解决过拟合，通过设置lamda参数，此处设置为1
plot_learning_curve(X_train_norm, y_train, X_val_norm, y_val, lamda=1)  # 绘制使用lamda之后的学习曲线误差图像

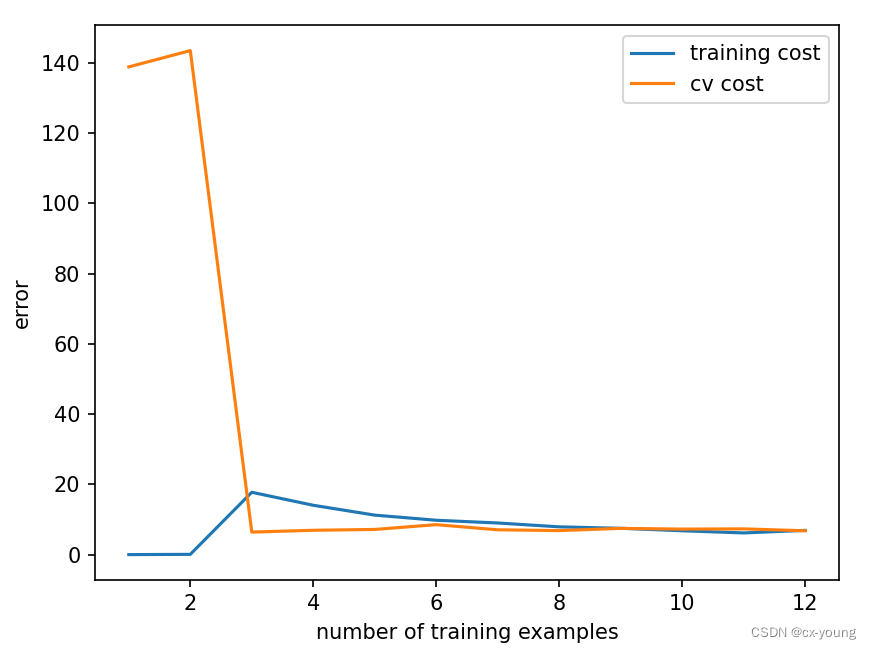
在这里插入图片描述
画出使用正则化之后的学习曲线误差函数。可以看出，此时训练集的误差仍然很低，但不是0了，而验证集的误差也降低到一个很低的状态

7.3将lamda设置为很大很大

# 将lamda调整为100，此时lamda过大，导致欠拟合
plot_learning_curve(X_train_norm, y_train, X_val_norm, y_val, lamda=100)  # 欠拟合

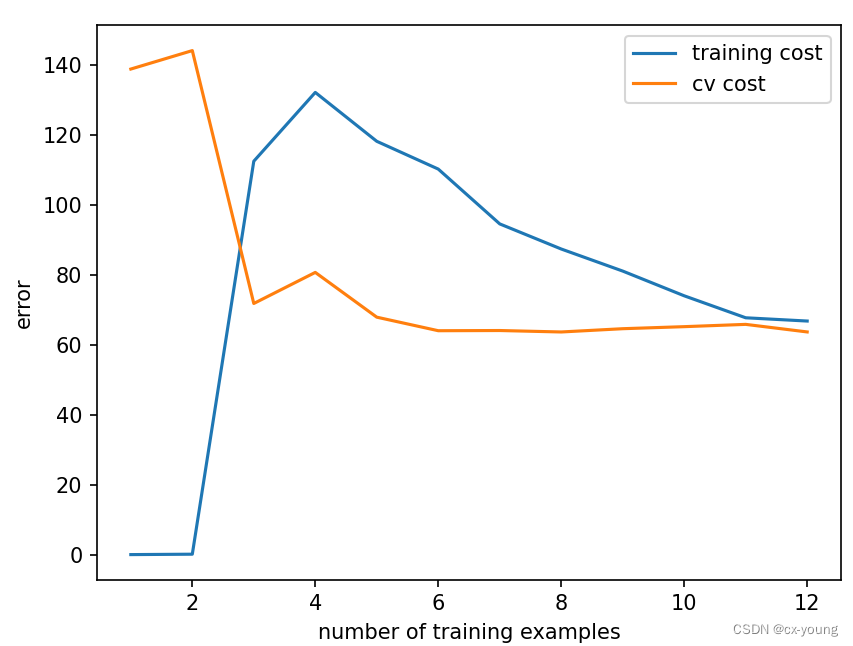
在这里插入图片描述

把lamda调整为很大时，这时训练集和验证集的误差会很接近，但是都会很大，此时是欠拟合

7.4设置一组lamda

那lamda应该要取多少合适？下面进行正则化参数lamda的选取

# 设定存储lamda参数的列表，进行正则化参数lamda的选取
lamdas = [0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]
training_cost = []
cv_cost = []
for lamda in lamdas:
    res = train_model(X_train_norm, y_train, lamda)

    tc = reg_cost(res, X_train_norm, y_train, lamda=0)  # lamda设置为0，因为reg_cost这一步还未进行正则化
    cv = reg_cost(res, X_val_norm, y_val, lamda=0)
    training_cost.append(tc)
    cv_cost.append(cv)
plt.plot(lamdas, training_cost, label='training cost')
plt.plot(lamdas, cv_cost, label='cv cost')
plt.legend()
# 设置横轴和纵轴的标签
plt.xlabel('lamdas')
plt.ylabel('cost')
plt.show()

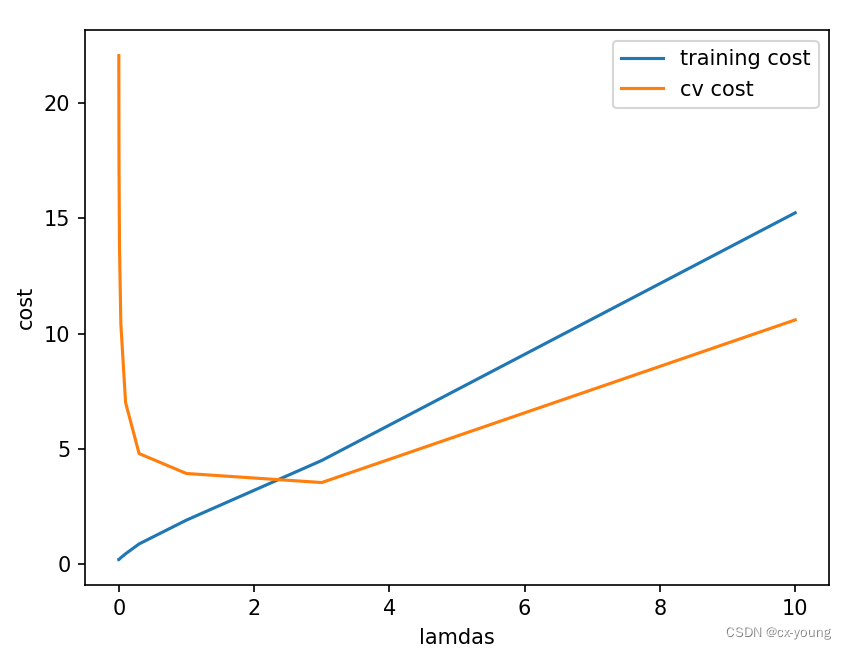
在这里插入图片描述
从图中可以看出lamda在2~4之间时的cv cost最小

7.5找出最小的cv_cost对应的lamda

# 找出最小的cv_cost对应的lamda
# 通过执行 np.argmin(cv_cost)，我们会得到最小成本值cv_cost的索引。然后，我们可以使用这个索引来访问 lamdas 列表，找到对应的正则化参数 lamda。
min_cost_cv = lamdas[np.argmin(cv_cost)]
print(min_cost_cv)  # 3

7.6将训练得到的参数应用到测试集上

res = train_model(X_train_norm, y_train, lamda=3)
test_cost = reg_cost(res, X_test_norm, y_test, lamda=0)
print(test_cost)  # 4.3976161577441975

完整代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
from scipy.optimize import minimize

'''在本练习中，您将实现正则化线性回归，并使用它来研究具有不同偏差-方差特性的模型。
在练习的前半部分，您将实现正则化线性回归，利用水库水位的变化来预测从大坝流出的水量。
在后半部分中，您将对调试学习算法进行一些诊断，并检查偏差和偏差的影响。'''
# 导入数据集
data = loadmat('ex5data1.mat')

# 打印data字典里的键  1. X和y训练集数据  2. Xtest和ytest是测试集数据  3.Xval和yval是验证集数据
# dict_keys(['__header__', '__version__', '__globals__', 'X', 'y', 'Xtest', 'ytest', 'Xval', 'yval'])
print('打印data字典里的键：',
      data.keys())  # 打印data字典里的键： dict_keys(['__header__', '__version__', '__globals__', 'X', 'y', 'Xtest', 'ytest', 'Xval', 'yval'])

# 训练集
X_train, y_train = data['X'], data['y']
print('打印训练集维度：', X_train.shape, y_train.shape)  # (12, 1) (12, 1) 表明有12个样本，1个特征

# 验证集
X_val, y_val = data['Xval'], data['yval']
print('打印验证集维度：', X_val.shape, y_val.shape)  # (21, 1) (21, 1)表明有21个样本，1个特征

# 测试集
X_test, y_test = data['Xtest'], data['ytest']
print('打印测试集维度：', X_test.shape, y_test.shape)  # (21, 1) (21, 1) 表明有21个样本，1个特征

# 插入一列，添加偏置项
X_train = np.insert(X_train, 0, 1, axis=1)
X_val = np.insert(X_val, 0, 1, axis=1)
X_test = np.insert(X_test, 0, 1, axis=1)

'''绘制散点图的函数 plot_data()。
它使用训练数据集的特征和标签来创建一个散点图，以可视化特征与标签之间的关系。'''


def plot_data():
    fig, ax = plt.subplots()  # 创建图形对象(fig)和一个坐标轴对象(ax)
    # 使用scatter函数绘制散点图，      X_train[:, 1]表示   使用训练数据集中第二列特征作为X轴坐标  水位的变化
    #                              y_train表示        使用训练数据集中的标签作为Y轴坐标      出水量
    # 按照每个样本的特征和标签的取值，在散点图显示它们之间的关系
    ax.scatter(X_train[:, 1], y_train)
    ax.set(xlabel='change in water level(x)',
           ylabel='water flowing out the dam(y)')


# 调用plot_data函数,看原始数据分布散点图
plot_data()

# 显示图形
plt.show()


# 损失函数
def reg_cost(theta, X, y, lamda):
    cost = np.sum(np.power((X @ theta - y.flatten()), 2))
    reg = theta[1:] @ theta[1:] * lamda  # 第一项不参与正则化
    return (cost + reg) / (2 * len(X))


# 测试 损失函数
# X_train.shape[1]表示训练数据集X_train的列数，也就是特征的个数。
# 然后，使用np.ones()函数创建了一个元素均为1的数组，并赋值给theta变量
# 模型参数初始化或迭代优化过程中的初始点。
theta = np.ones(X_train.shape[1])
lamda = 1
result_cost = reg_cost(theta, X_train, y_train, lamda)

print(result_cost)  # 303.9931922202643


# 梯度
def reg_gradient(theta, X, y, lamda):
    grad = (X @ theta - y.flatten()) @ X
    reg = lamda * theta
    reg[0] = 0  # 不改变维度，直接赋值为0第一行不参与运算
    return (grad + reg) / (len(X))


# 测试梯度
result_gradient = reg_gradient(theta, X_train, y_train, lamda)

print(result_gradient)  # [-15.30301567 598.25074417]

# 这个训练过程可以用来训练各种不同的机器学习模型，如线性回归、逻辑回归等
'''参数特征矩阵 X、目标变量 y 和正则化参数 lambda 作为输入，并返回通过最小化代价函数得到的模型参数 theta
theta = np.ones(X.shape[1]): 初始化模型参数theta，将其设置为全1数组，X.shape[1]表示 X列数 即特征的数量
res = minimize...:使用优化算法minimize()最小化损失函数fun，并得到最优的模型参数'''


def train_model(X, y, lamda):
    theta = np.ones(X.shape[1])
    res = minimize(fun=reg_cost,  # 损失函数
                   x0=theta,  # 初始参数值
                   args=(X, y, lamda),  # 附加参数
                   method='TNC',  # 使用TNC算法进行优化
                   jac=reg_gradient)  # 表示损失函数的梯度函数
    return res.x  # 返回通过优化算法得到的最优模型参数theta


# lamda目前不使用，因为是线性模型不会过拟合
theta_final = train_model(X_train, y_train, lamda=0)

# 使用线性回归拟合数据
# 调用plot_data函数
plot_data()
# x轴只取第2列
plt.plot(X_train[:, 1], X_train @ theta_final, c='r')
plt.show()  # 查看会发现，偏差非常大，处于欠拟合的状态


# 任务：训练样本从1开始递增进行训练，比较训练集和验证集上的损失函数的变化情况，观察一下误差的变化情况
# 定义一个函数展现整个学习过程，即随着样本数量的增加，巡礼那几成本和验证集成本的学习误差的曲线
def plot_learning_curve(X_train, y_train, X_val, y_val, lamda):
    # 使用列表x存放训练样本的个数
    x = range(1, len(X_train) + 1)
    # 再定义两个空列表分别存放：验证集和训练集损失函数
    training_cost = []
    cv_cost = []
    # 遍历x中的每个元素，表述不断增加训练样本的数量来计算学习曲线
    for i in x:
        # 调用train_model()函数，输入前i个训练样本和相应的目标值，以及正则化参数lamda，返回模型的参数结果res
        # X_train[:i, :]将返回训练数据集中的前 i 行的所有列
        res = train_model(X_train[:i, :], y_train[:i, :], lamda)
        # 调用reg_cost()函数，计算使用前i个训练样本拟合得到的模型在训练集上的损失函数值
        train_cost_i = reg_cost(res, X_train[:i, :], y_train[:i, :], lamda)
        # 调用reg_cost()函数，计算使用前i个训练样本拟合得到的模型在验证集上的损失函数值
        cv_cost_i = reg_cost(res, X_val, y_val, lamda)
        # 将训练集和验证集的损失函数值分别添加到两个列表中
        training_cost.append(train_cost_i)
        cv_cost.append(cv_cost_i)
    # 横轴为训练样本的数量 x，纵轴为对应的训练集和验证集的损失函数值。
    plt.plot(x, training_cost, label='training cost')
    plt.plot(x, cv_cost, label='cv cost')
    # 显示图例，标明不同曲线的含义
    plt.legend()
    # 设置横轴和纵轴的标签
    plt.xlabel('number of training examples')
    plt.ylabel('error')
    # 显示绘制的学习曲线图
    plt.show()


# 传入相应的训练集、验证集以及正则化参数，可以绘制出学习曲线来评估模型的性能和训练集大小对模型的影响
plot_learning_curve(X_train, y_train, X_val, y_val, lamda=0)
# 由图可知，随着样本数量的增加，训练集成本的误差逐渐上升，而验证集成本误差逐渐下降。
# 目前训练集和验证集的误差都比较高，表示模型欠拟合

# 上述简单的线性模型导致了欠拟合，存在高偏差如何解决？
# 任务：构造多项式特征（将原本只有一列的特征x通过生成高阶次项创造多个特征），进行多项式回归
'''多项式特征生成函数
X：传入特征矩阵X和多项式阶数power
用于生成具有不同阶数多项式特征的新特征矩阵，帮助模型更好拟合非线性关系'''


def poly_feature(X, power):
    for i in range(2, power + 1):  # 循环从2到给定的多项式阶数power+1
        # 在输入特征矩阵X 的最后一列插入一列
        # 首先使用 np.power() 函数计算原始特征矩阵 X 的第二列（索引为 1）的 i 次方。X[:, 1] 表示取出矩阵 X 的所有行的第二列。
        # 然后，使用 np.insert() 函数将得到的新特征插入到矩阵 X 的最后一列。具体而言，X.shape[1] 返回 X 的列数，即特征的数量，axis=1 表示按列方向插入数据。
        # 通过这样的操作，我们将生成新的特征矩阵 X，其中包含了原始特征的不同次幂的组合。
        X = np.insert(X, X.shape[1], np.power(X[:, 1], i), axis=1)
    return X


'''计算特征矩阵 X 的每个特征的均值和方差
这些统计信息在数据处理中经常被用来进行特征缩放、归一化等操作，以提高模型训练的效果
计算均值和方差时应使用训练集的统计信息'''


def get_means_stds(X):
    # 使用 np.mean() 函数计算特征矩阵 X 沿着轴 0（列）的均值。
    # 这意味着函数将对特征矩阵 X 的每列进行均值和标准差的计算，也就是计算每个特征的均值和标准差。
    # 返回一个包含每个特征的均值的数组 means
    means = np.mean(X, axis=0)
    # 方差
    stds = np.std(X, axis=0)
    return means, stds


'''
特征归一化函数，接收特征矩阵X，均值数组means、方差数组stds作为输入
并返回归一化后的特征矩阵X
注：特征归一化是一种常见的数据预处理操作，可以提高模型训练效果，并确保不同特征之间的尺度差异不会对模型产生不良影响
通常情况下，归一化处理使用训练集进行'''


def feature_normalize(X, means, stds):
    # 第一列假设为常数项或类别信息，不需要进行归一化操作
    X[:, 1:] = (X[:, 1:] - means[1:]) / stds[1:]
    return X


# 测试
power = 6
# 对训练集、验证集、测试集分别调用 多项式特征生成函数
X_train_poly = poly_feature(X_train, power)
X_val_poly = poly_feature(X_val, power)
X_test_poly = poly_feature(X_test, power)
# 获取训练集的均值和方差
train_means, train_stds = get_means_stds(X_train_poly)
# 对训练集、验证集、测试集进行归一化处理
X_train_norm = feature_normalize(X_train_poly, train_means, train_stds)
X_val_norm = feature_normalize(X_val_poly, train_means, train_stds)
X_test_norm = feature_normalize(X_test_poly, train_means, train_stds)
# 获取最优的theta参数
theta_fit = train_model(X_train_norm, y_train, lamda=0)

'''绘制多项式拟合曲线的函数 plot_poly_fit()。
首先调用了之前定义的 plot_data() 函数，将训练数据集的散点图显示在图形界面中。然后使用训练得到的最优模型参数 theta_fit，在图形界面中绘制多项式拟合曲线'''


def plot_poly_fit():
    # 调用其可以在图形界面中显示训练集的散点图，帮助我们观察特征和标签之间的关系
    # 对于理解数据集、探索数据、以及选择适当的模型都非常有帮助
    plot_data()

    x = np.linspace(-60, 60, 100)  # 生成一个包含100个等间距数值的数组，范围从-60到60。这个数组将作为 X 轴的取值范围
    xx = x.reshape(100, 1)  # 将数组 x 进行形状变换，改为一个100行1列的二维数组。这样做是为了满足多项式特征的输入格式要求
    xx = np.insert(xx, 0, 1, axis=1)  # 在数组 xx 的第一列插入全1的列向量。这是为了与之前的训练数据集保持一致，添加了一个截距项
    xx = poly_feature(xx, power)  # 将原始特征矩阵 xx 转化为多项式特征矩阵。这样可以根据多项式的阶数 power 扩展特征
    xx = feature_normalize(xx, train_means,
                           train_stds)  # 对多项式特征矩阵 xx 进行归一化处理。这里使用训练数据集的均值 train_means和方差train_stds 进行归一化，保证与之前的训练数据集保持一致
    plt.plot(x, xx @ theta_fit,
             'r--')  # 绘制多项式拟合曲线，x为 X 轴，xx @ theta_fit 表示通过最优模型参数 theta_fit 对多项式特征矩阵 xx 进行预测得到的 Y 轴坐标。'r--' 表示以红色虚线的形式进行绘制
    plt.show()


# 通过调用 plot_poly_fit() 函数，可以在图形界面中显示训练数据集的散点图，并绘制多项式拟合曲线。这有助于直观地观察拟合效果，并评估模型的性能。
plot_poly_fit()

# 正则化影响 lamda设为0，因为正则化只在训练时才有
# 通过绘制学习曲线的误差函数，来看出它在训练集和验证集上表现为过拟合
plot_learning_curve(X_train_norm, y_train, X_val_norm, y_val, lamda=0)  # 高方差，过拟合

# 使用正则化解决过拟合，通过设置lamda参数，此处设置为1
plot_learning_curve(X_train_norm, y_train, X_val_norm, y_val, lamda=1)  # 绘制使用lamda之后的学习曲线误差图像

# 将lamda调整为100，此时lamda过大，导致欠拟合
plot_learning_curve(X_train_norm, y_train, X_val_norm, y_val, lamda=100)  # 欠拟合

# 设定存储lamda参数的列表，进行正则化参数lamda的选取
lamdas = [0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]
training_cost = []
cv_cost = []
for lamda in lamdas:
    res = train_model(X_train_norm, y_train, lamda)

    tc = reg_cost(res, X_train_norm, y_train, lamda=0)  # lamda设置为0，因为reg_cost这一步还未进行正则化
    cv = reg_cost(res, X_val_norm, y_val, lamda=0)
    training_cost.append(tc)
    cv_cost.append(cv)
plt.plot(lamdas, training_cost, label='training cost')
plt.plot(lamdas, cv_cost, label='cv cost')
plt.legend()
# 设置横轴和纵轴的标签
plt.xlabel('lamdas')
plt.ylabel('cost')
plt.show()
# 找出最小的cv_cost对应的lamda
# 通过执行 np.argmin(cv_cost)，我们会得到最小成本值cv_cost的索引。然后，我们可以使用这个索引来访问 lamdas 列表，找到对应的正则化参数 lamda。
min_cost_cv = lamdas[np.argmin(cv_cost)]
print(min_cost_cv)  # 3
res = train_model(X_train_norm, y_train, lamda=3)
test_cost = reg_cost(res, X_test_norm, y_test, lamda=0)
print(test_cost)  # 4.3976161577441975