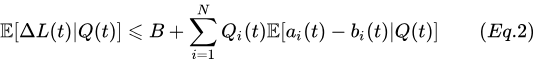文章目录
- 正文
- 引言
- Lyapunov drift for queueing networks 排队网络的Lyapunov漂移
- Quadratic Lyapunov functions 二次李雅普诺夫函数
- Bounding the Lyapunov drift 李亚普诺夫漂移的边界
- A basic Lyapunov drift theorem 一个基本的李雅普诺夫漂移定理
- Lyapunov optimization for queueing networks 排队网络的Lyapunov优化
- 参考资料
正文
本文描述了动力系统的李雅普诺夫优化。(动力系统:随时间变化的系统)
给出了在排队网络最优控制中的应用实例。
引言
李雅普诺夫优化是指利用李雅普诺夫函数对动力系统进行最优控制。
李雅普诺夫函数在控制理论中被广泛应用于保证不同形式的系统稳定性。
系统在特定时间的状态通常用多维向量来描述。
李雅普诺夫函数是这种多维状态的一个非负标量度量(a nonnegative scalar measure)。
通常,函数被定义为当系统走向不希望的状态时变大。
系统稳定性是通过采取控制动作使李雅普诺夫函数在负方向上向零漂移来实现的。
李雅普诺夫漂移是研究排队网络最优控制的核心。
一个典型的目标是稳定所有网络队列,同时优化某些性能目标,例如最小化平均能量或最大化平均吞吐量。
最小化二次Lyapunov函数的漂移对应用于网络稳定性的backpressure routing算法,也称为最大权重算法。[1][2]
在Lyapunov漂移中加入加权惩罚项并使其和最小化,得到了用于联合网络稳定性和惩罚最小化的漂移+惩罚算法。[3][4][5]
漂移加惩罚过程也可用于计算凸规划和线性规划的解。[6]
Lyapunov drift for queueing networks 排队网络的Lyapunov漂移
考虑一个随着具有标准化时隙
t
∈
{
0
,
1
,
2
,
.
.
.
}
t∈\{0,1,2,...\}
t∈{0,1,2,...}的离散时间变化的排队网络。
假设网络中有
N
N
N 个队列,并定义在时间
t
t
t 时队列积压向量为
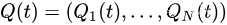
Quadratic Lyapunov functions 二次李雅普诺夫函数
对于每个时隙,定义
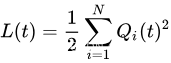
该函数是网络中总队列积压的标量度量。它被称为关于队列状态的二次Lyapunov函数。
将李雅普诺夫漂移定义为该函数从一个时隙到下一个时隙的变化:
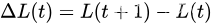
Bounding the Lyapunov drift 李亚普诺夫漂移的边界
假设队列积压根据以下等式随时间变化:
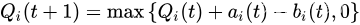
其中,
a
i
(
t
)
a_{i}(t)
ai(t)和
b
i
(
t
)
b_{i}(t)
bi(t)分别为时隙
t
t
t 上队列
i
i
i 的到达和服务机会。该式可用于计算任意时隙
t
t
t 上的Lyapunov漂移的边界:
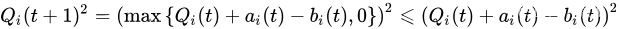
由上式推出:
Δ
L
(
t
)
=
L
(
t
+
1
)
−
L
(
t
)
=
1
2
∑
i
=
1
N
(
Q
i
(
t
+
1
)
2
−
Q
i
(
t
)
2
)
≤
1
2
∑
i
=
1
N
(
(
Q
i
(
t
)
+
a
i
(
t
)
−
b
i
(
t
)
)
2
−
Q
i
(
t
)
2
)
≤
1
2
∑
i
=
1
N
(
a
i
(
t
)
+
b
i
(
t
)
)
2
+
∑
i
=
1
N
Q
i
(
t
)
(
a
i
(
t
)
−
b
i
(
t
)
)
\Delta L(t)= L(t+1)-L(t)\\=\frac{1}{2}\sum_{i=1}^{N}(Q_i(t+1)^2-Q_i(t)^2)\\\le\frac{1}{2}\sum_{i=1}^{N}((Q_i(t)+a_i(t)-b_i(t))^2-Q_i(t)^2)\\\le\frac{1}{2}\sum_{i=1}^{N}(a_i(t)+b_i(t))^2+\sum_{i=1}^{N}Q_i(t)(a_i(t)-b_i(t))
ΔL(t)=L(t+1)−L(t)=21∑i=1N(Qi(t+1)2−Qi(t)2)≤21∑i=1N((Qi(t)+ai(t)−bi(t))2−Qi(t)2)≤21∑i=1N(ai(t)+bi(t))2+∑i=1NQi(t)(ai(t)−bi(t))
记
B
(
t
)
=
1
2
∑
i
=
1
N
(
a
i
(
t
)
+
b
i
(
t
)
)
2
B(t)=\frac{1}{2}\sum_{i=1}^{N}(a_i(t)+b_i(t))^2
B(t)=21∑i=1N(ai(t)+bi(t))2,则有
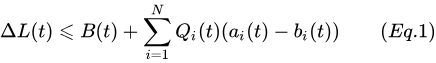
其中:
假设每个队列的到达和服务这两项是有界的,因此存在一个有限常数
B
>
0
B>0
B>0,使得对于所有
t
t
t 和所有可能的队列向量
Q
(
t
)
Q(t)
Q(t) 都成立如下性质:
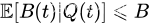
取(Eq. 1)的条件期望,得到Lyapunov漂移的条件期望的边界如下:
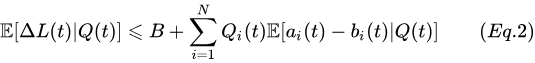
A basic Lyapunov drift theorem 一个基本的李雅普诺夫漂移定理
在许多情况下,网络可以被控制,因此每个队列的到达和服务之间的差异对某个实数
ε
>
0
\varepsilon>0
ε>0 满足以下的性质:
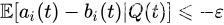
如果上式对于所有队列
i
i
i、所有时隙
t
t
t 和所有可能的向量
Q
(
t
)
\displaystyle Q(t)
Q(t) 对相同ε成立,则(等式2)简化为以下李亚普诺夫漂移定理中使用的漂移条件。
下面的定理可以看作是马尔可夫链的Foster定理的一个变体。然而,它不需要马尔可夫链结构。
定理(Lyapunov Drift):
假设存在常数
B
≥
0
,
ε
>
0
B\ge0,\varepsilon>0
B≥0,ε>0 使得对于所有的
t
t
t 和可能的向量
Q
(
t
)
Q(t)
Q(t) ,条件李雅普诺夫漂移满足:
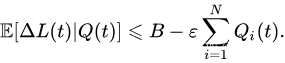
注等式2.
则对所有的时隙
t
>
0
t>0
t>0,网络中的时间平均队列大小满足:
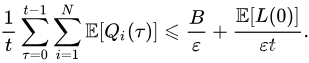
证明:
取漂移不等式两边的期望,利用迭代期望定律,得到:
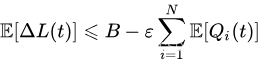
将上式对
τ
∈
{
0
,
1
,
.
.
.
,
t
−
1
}
\tau∈\{0,1,...,t-1\}
τ∈{0,1,...,t−1} 求和,利用可伸缩和定律,得到:
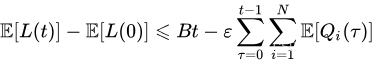
利用
L
(
t
)
L(t)
L(t) 非负的事实,重新排列上式中的各项,证明了结果。
Lyapunov optimization for queueing networks 排队网络的Lyapunov优化
考虑与上一节相同的排队网络。
现在定义
p
(
t
)
p(t)
p(t) 作为在时隙
t
t
t 上产生的网络惩罚。
假设目标是稳定排队网络,同时最小化
p
(
t
)
p(t)
p(t) 的时间平均值。
例如,为了稳定网络,同时最小化时间平均功率, p ( t ) p (t) p(t) 可定义为网络在时隙 t t t 上产生的总功率。处理某些理想报酬 r ( t ) r(t) r(t) 的时间平均值最大化的问题,可以定义惩罚 p ( t ) = − r ( t ) p(t)=-r(t) p(t)=−r(t)。这对于在保证稳定性的前提下最大化整个网络的效用是很有用的。
在稳定网络的同时最小化惩罚
p
(
t
)
p(t)
p(t) 的平均时间,网络算法可以设计成使控制动作贪婪地最小化下面每个时隙上的漂移加惩罚表达式的边界:
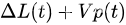
其中
V
V
V 是一个非负的权重,可以根据需要选择它来影响性能权衡。这种方法的一个关键特征是,它通常不需要了解随机网络事件(例如随机作业到达或通道实现)的概率。选择
V
=
0
V=0
V=0 可简化为最小化每个槽漂移的边界,对于多跳队列网络中的路由,可简化为Tassiulas和Ephremides开发的背压路由算法。
使用
V
=
0
V=0
V=0 并定义
p
(
t
)
p(t)
p(t) 为插槽
t
t
t 上的网络功耗引出了Neely提出的在保证网络稳定性的前提下最小化平均功率的漂移加惩罚算法[8]。
使用
V
=
0
V=0
V=0 并使用
p
(
t
)
p(t)
p(t) 作为允许控制效用度量的负值,引出了Neely、Modiano和Li开发的用于联合流量控制和网络路由的漂移加惩罚算法。
在这种情况下,前一节的李雅普诺夫漂移定理的推广是重要的。为了说明简单,假设
p
(
t
)
p(t)
p(t) 有界于下:

例如,上面满足
p
m
i
n
=
0
p_{min}=0
pmin=0 在这种情况下
p
(
t
)
p(t)
p(t) 总是非负的。让
p
∗
p^{*}
p∗ 表示
p
(
t
)
p(t)
p(t) 的时间平均值的期望目标。
令
V
V
V 是一个参数,用来衡量达到目标的重要性。以下定理表明,如果满足漂移+惩罚条件,则时间平均惩罚最多比期望目标高出O(1/V),而平均队列大小为O(V)。
V
V
V 参数可以调优,使平均时间惩罚尽可能接近(或低于)所需的目标,并进行相应的队列大小权衡。
定理(Lyapunov Optimization)
假设存在常数
ε
>
0
,
V
,
B
≥
0
\varepsilon>0,V,B\ge0
ε>0,V,B≥0 以及
p
∗
p^*
p∗ 对于所有的
t
t
t 和所有可能的向量
Q
(
t
)
Q(t)
Q(t) ,以下漂移加惩罚条件成立:
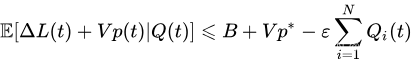
则对于所有
t
>
0
t>0
t>0 ,时间平均惩罚和时间平均队列大小满足:
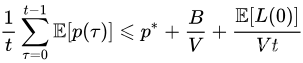
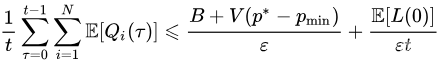
证明
取假定漂移加惩罚的两边的期望并使用迭代期望定律,我们得到:
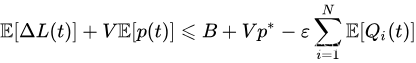
在前
t
t
t 个时隙上求和,并且使用伸缩和定律给出:
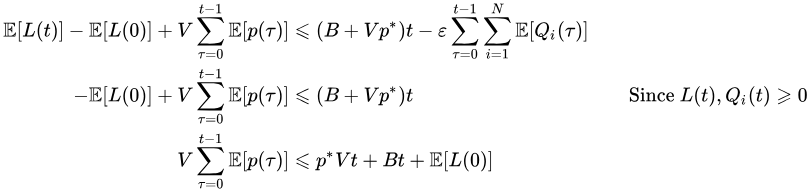
除以
V
t
{\displaystyle Vt}
Vt 并且重新排列项证明了时间平均惩罚边界。一个类似的论证证明了时间平均队列大小边界。
参考资料
https://en.wikipedia.org/wiki/Lyapunov_optimization