《Uncovering mesa-optimization algorithms in Transformers》

论文链接：https://arxiv.org/abs/2309.05858

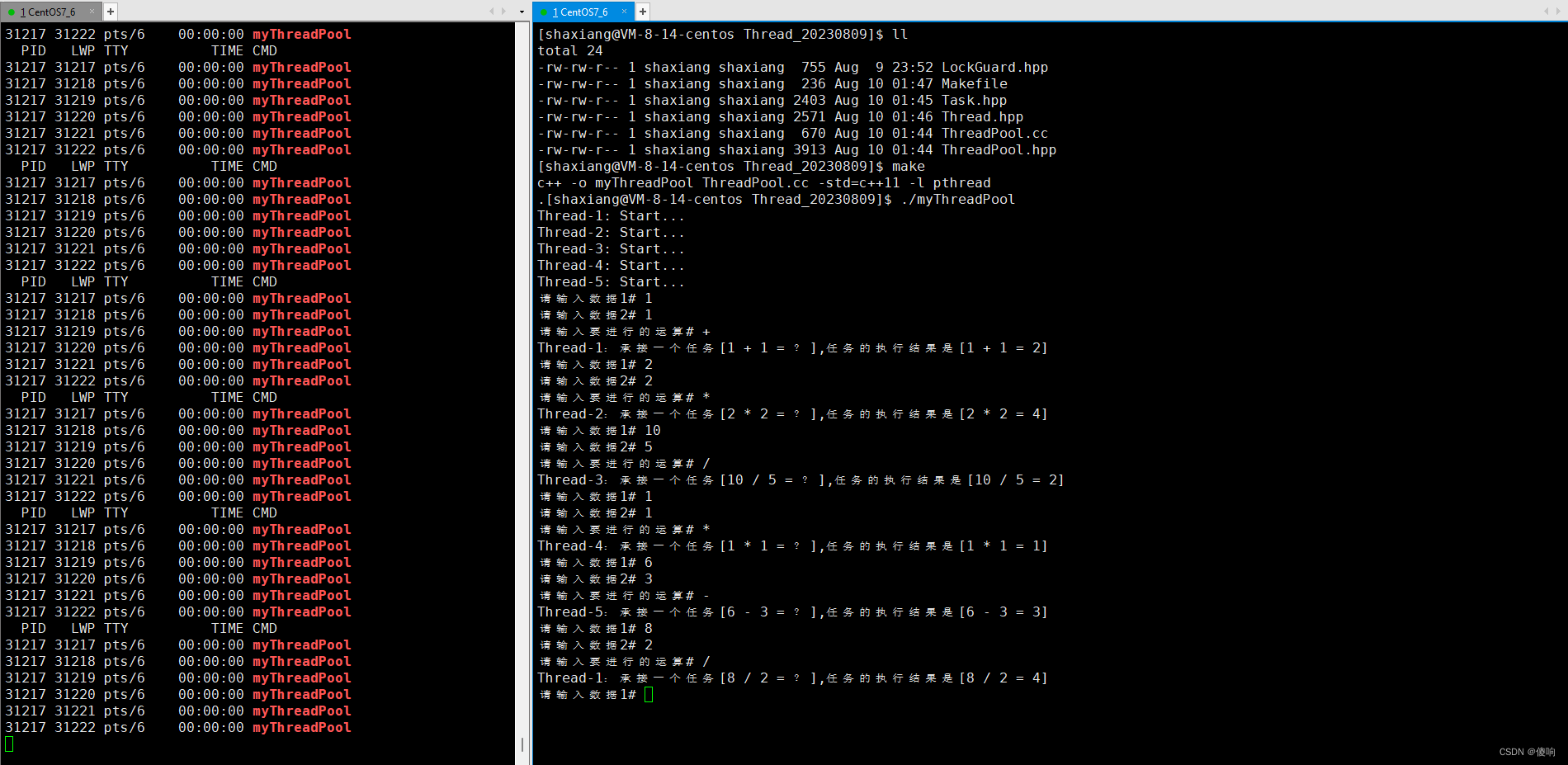
为什么 transformer 性能这么好？它给众多大语言模型带来的上下文学习 (In-Context Learning) 能力是从何而来？在人工智能领域里，transformer 已成为深度学习中的主导模型，但人们对于它卓越性能的理论基础却一直研究不足。
最近，来自 Google AI、苏黎世联邦理工学院、Google DeepMind 研究人员的新研究尝试为我们揭开谜底。在新研究中，他们对 transformer 进行了逆向工程，寻找到了一些优化方法。

作者证明，最小化通用自回归损失会产生在 Transformer 的前向传递中运行的基于辅助梯度的优化算法。这种现象最近被称为「mesa 优化（mesa-optimization）」。此外，研究人员发现所得的 mesa 优化算法表现出上下文中的小样本学习能力，与模型规模无关。因此，新的结果对此前大语言模型中出现的小样本学习的原理进行了补充。

研究人员认为：Transformers 的成功基于其在前向传递中实现 mesa 优化算法的架构偏差：(i) 定义内部学习目标，以及 (ii) 对其进行优化。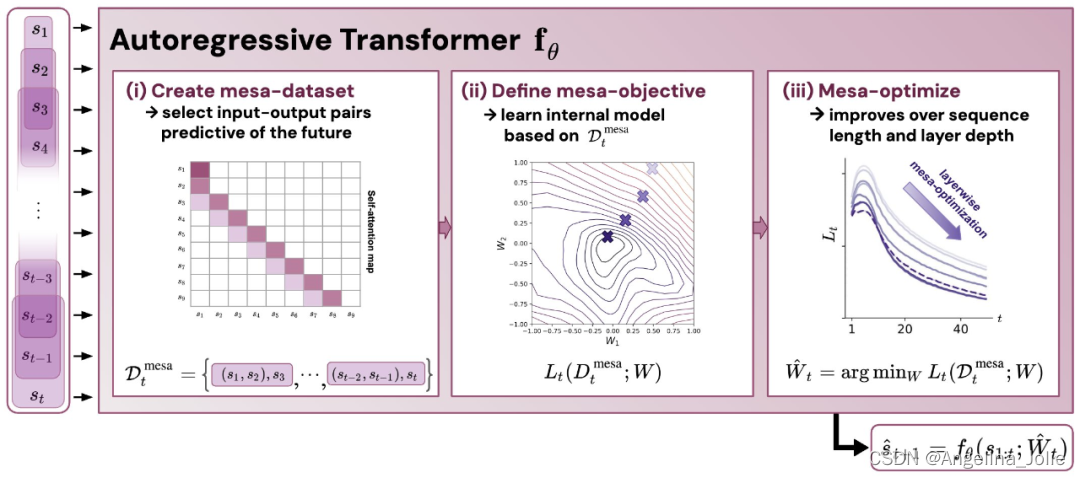

图 1：新假设的说明：优化自回归 Transformer fθ 的权重 θ 会产生在模型前向传播中实现的 mesa 优化算法。作为输入序列 s_1, . 。。， s_t 被处理到时间步 t，Transformer (i) 创建一个由输入 - 目标关联对组成的内部训练集，(ii) 通过结果数据集定义内部目标函数，用于衡量内部模型的性能 使用权重 W，(iii) 优化该目标并使用学习的模型生成未来的预测。 

该研究的贡献包括：

• 概括了 von Oswald 等人的理论，并展示了从理论上，Transformers 是如何通过使用基于梯度的方法优化内部构建的目标来自回归预测序列下一个元素的。

• 通过实验对在简单序列建模任务上训练的 Transformer 进行了逆向工程，并发现强有力的证据表明它们的前向传递实现了两步算法：(i) 早期自注意力层通过分组和复制标记构建内部训练数据集，因此隐式地构建内部训练数据集。定义内部目标函数，(ii) 更深层次优化这些目标以生成预测。

• 与 LLM 类似，实验表明简单的自回归训练模型也可以成为上下文学习者，而即时调整对于改善 LLM 的上下文学习至关重要，也可以提高特定环境中的表现。

• 受发现注意力层试图隐式优化内部目标函数的启发，作者引入了 mesa 层，这是一种新型注意力层，可以有效地解决最小二乘优化问题，而不是仅采取单个梯度步骤来实现最优。实验证明单个 mesa 层在简单的顺序任务上优于深度线性和 softmax 自注意力 Transformer，同时提供更多的可解释性。

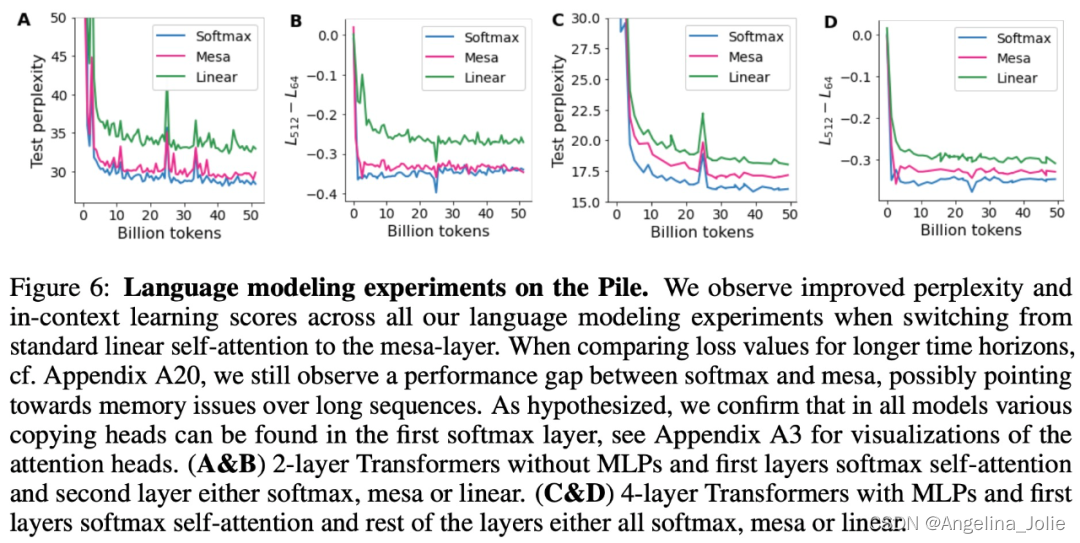
• 在初步的语言建模实验后发现，用 mesa 层替换标准的自注意力层获得了有希望的结果，证明了该层具有强大的上下文学习能力。

基于最近人们的工作表明，经过明确训练来解决上下文中的小样本任务的 transformer 可以实现梯度下降（GD）算法。在这里，作者展示了这些结果可以推广到自回归序列建模 —— 这是训练 LLM 的典型方法。

首先分析在简单线性动力学上训练的 transformer，其中每个序列由不同的 W* 生成 - 以防止跨序列记忆。在这个简单的设置中，作者展示了 transformer 创建 mesa 数据集，然后使用预处理的 GD 优化 mesa 目标。

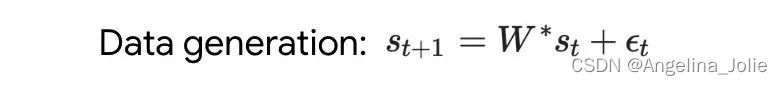
该研究在聚合相邻序列元素的 token 结构上训练深度 transformer。有趣的是，这种简单的预处理会产生极其稀疏的权重矩阵（只有不到 1% 的权重非零），从而产生逆向工程算法。

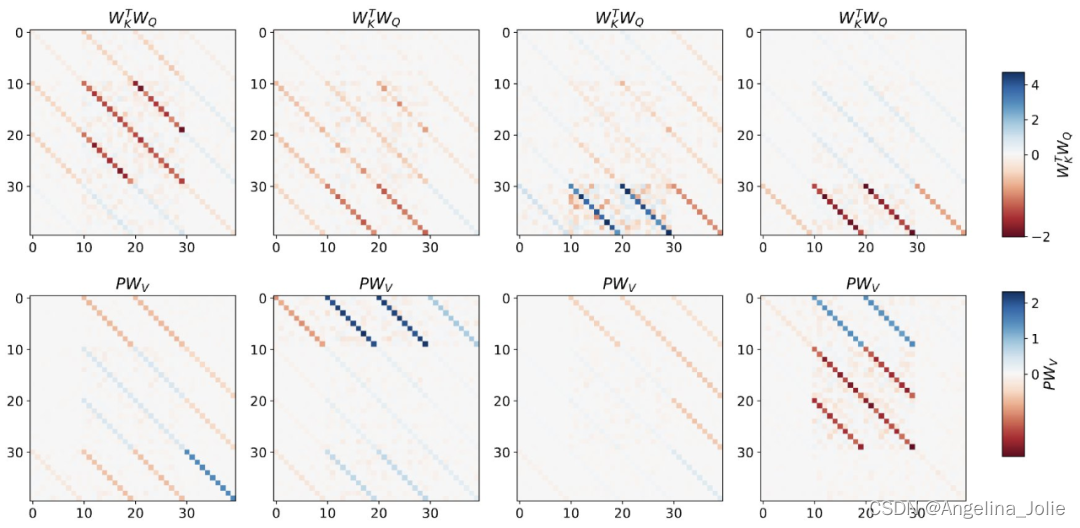
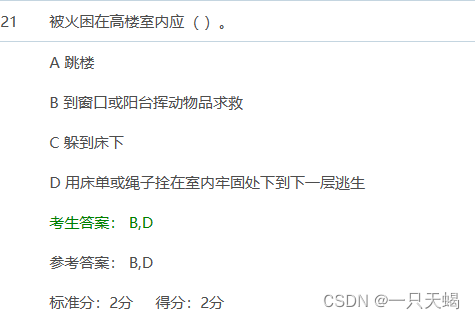
对于单层线性自注意力，权重对应一个 GD 步骤。对于深度 transformer，可解释性就变得困难。该研究依靠线性探测并检查隐藏激活是否可以预测自回归目标或预处理输入。

有趣的是，两种探测方法的可预测性都会随着网络深度的增加而逐渐提高。这一发现表明模型中隐藏着预处理的 GD。

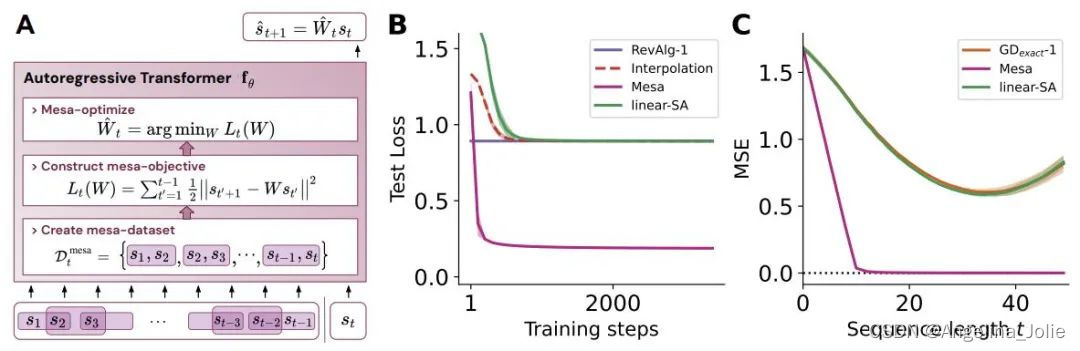
图 2：对经过训练的线性自注意力层进行逆向工程。

该研究发现，在构建中使用所有自由度时，可以完美地拟合训练层，不仅包括学习的学习率 η，还包括一组学习的初始权重 W_0。重要的是，如图 2 所示，学得的 one-step 算法的性能仍然远远优于单个 mesa 层。

我们可以注意到，在简单的权重设置下，很容易通过基础优化发现，该层可以最优地解决此处研究的任务。该结果证明了硬编码归纳偏差有利于 mesa 优化的优势。

凭借对多层案例的理论见解，先分析深度线性和 softmax 仅注意 Transformer。作者根据 4 通道结构设置输入格式，

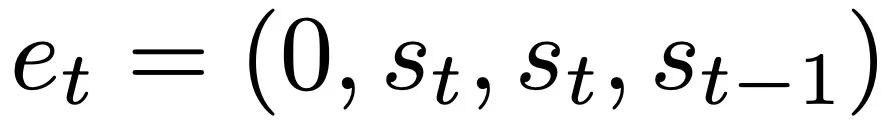
，这对应于选择 W_0 = 0。

与单层模型一样，作者在训练模型的权重中看到了清晰的结构。作为第一个逆向工程分析，该研究利用这个结构并构建一个算法（RevAlg-d，其中 d 表示层数），每个层头包含 16 个参数（而不是 3200 个）。作者发现这种压缩但复杂的表达式可以描述经过训练的模型。特别是，它允许以几乎无损的方式在实际 Transformer 和 RevAlg-d 权重之间进行插值。

虽然 RevAlg-d 表达式解释了具有少量自由参数的经过训练的多层 Transformer，但很难将其解释为 mesa 优化算法。因此，作者采用线性回归探测分析（Alain & Bengio，2017；Akyürek et al.，2023）来寻找假设的 mesa 优化算法的特征。

在图 3 所示的深度线性自注意力 Transformer 上，我们可以看到两个探针都可以线性解码，解码性能随着序列长度和网络深度的增加而增加。因此，基础优化发现了一种混合算法，该算法在原始 mesa-objective Lt (W) 的基础上逐层下降，同时改进 mesa 优化问题的条件数。这导致  mesa-objective Lt (W) 快速下降。此外可以看到性能随着深度的增加而显着提高。

因此可以认为自回归 mesa-objective Lt (W) 的快速下降是通过对更好的预处理数据进行逐步（跨层）mesa 优化来实现的。

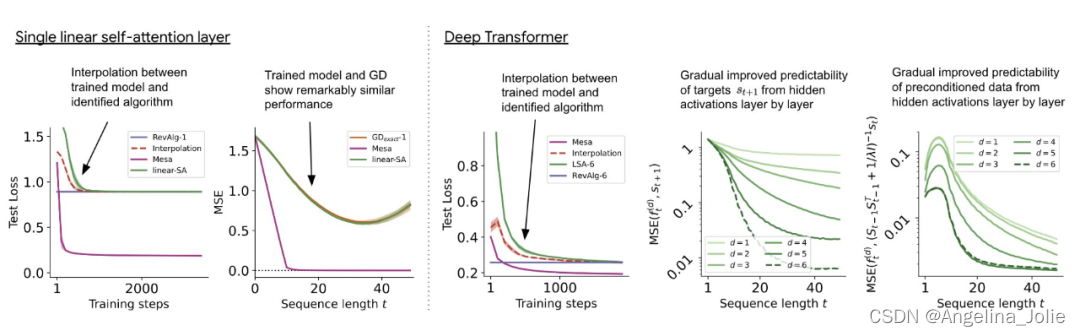
图 3：对构建的 token 输入进行逆向工程的多层 Transformer 训练。 

这表明，如果 transformer 在构建的 token 上进行训练，它就会通过 mesa 优化进行预测。有趣的是，当直接给出序列元素时，transformer 会自行通过对元素进行分组来构造 token，研究团队将其称为「创建 mesa 数据集」。

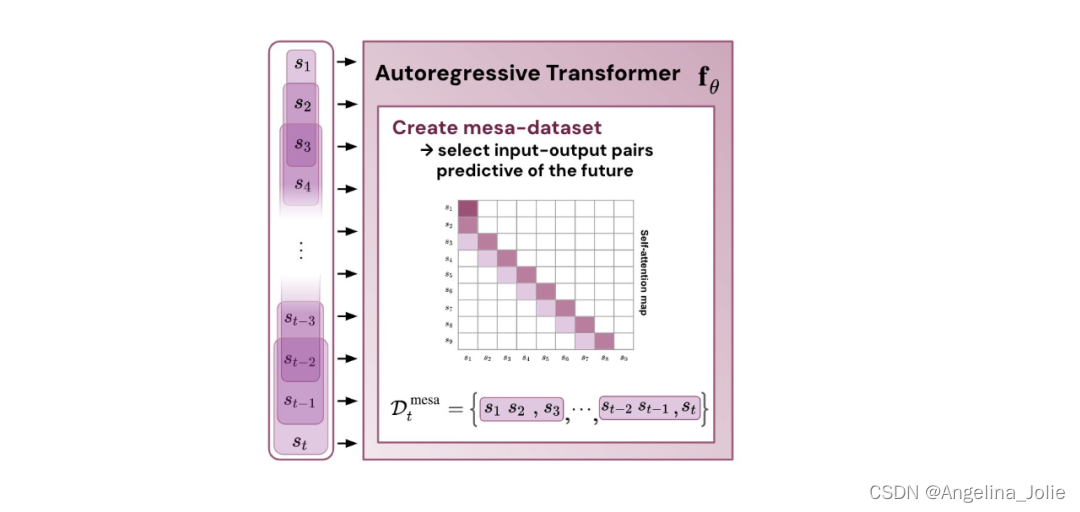
结论

该研究表明，当在标准自回归目标下针对序列预测任务进行训练时，Transformer 模型能够开发基于梯度的推理算法。因此，在多任务、元学习设置下获得的最新结果也可以转化到传统的自监督 LLM 训练设置中。

此外，该研究还发现学得的自回归推理算法可以在无需重新训练的情况下重新调整用途，以解决有监督的上下文学习任务，从而在单个统一框架内解释结果。

那么，这些与上下文学习（in-context learning）有什么关系呢？该研究认为：在自回归序列任务上训练 transformer 后，它实现了适当的 mesa 优化，因此可以进行少样本（few-shot）上下文学习，而无需任何微调。

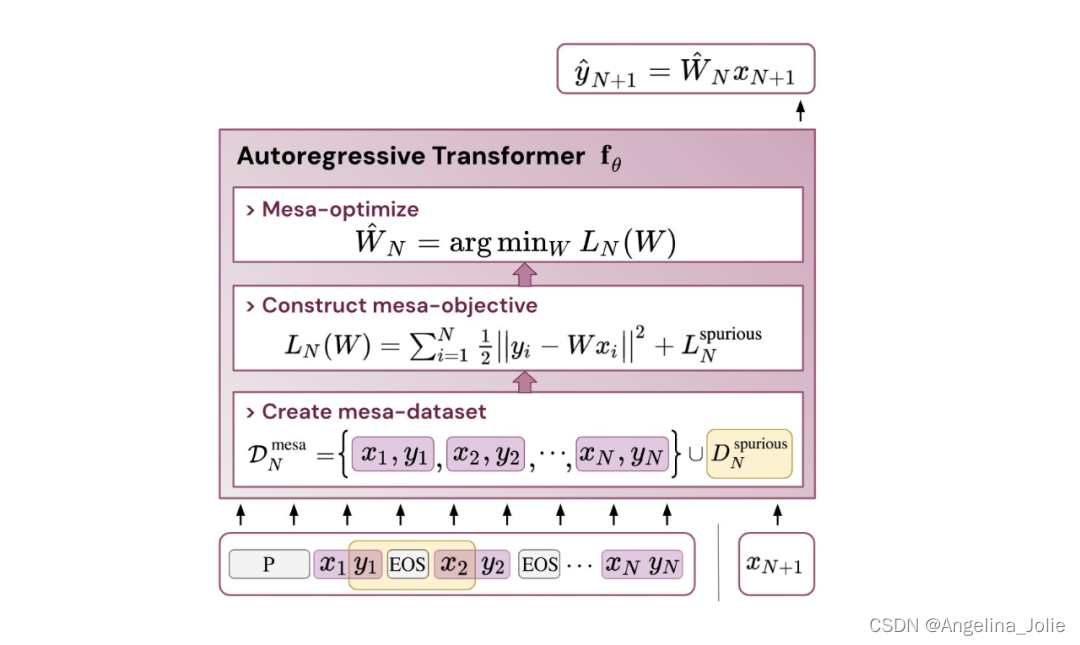
该研究假设 LLM 也存在 mesa 优化，从而提高了其上下文学习能力。有趣的是，该研究还观察到，为 LLM 有效调整 prompt 也可以带来上下文学习能力的实质性改进。