注意力是人类认知功能的重要组成部分，当面对海量的信息时，人类可以在关注一些信息的同时，忽略另一些信息。当计算机使用神经网络来处理大量的输入信息时，也可以借鉴人脑的注意力机制，只选择一些关键的信息输入进行处理，来提高神经网络的效率。

2017年，谷歌团队的Vaswani等人发表的《Attention Is All You Need》利用注意力机制，提出Transformer机器学习框架。到目前为止，该论文已经被引用9万多次，显示出Transformer构架和注意力机制在现代机器学习领域中得到了广泛应用。

注意力机制的一个核心步骤中包含了一个 softmax函数，其作用是产生 token 的一个概率分布。数学上来讲，Softmax函数的定义很简单，就是将一个任意序列的数组转换成区间为（0,1）的数组（图1）。因为这种归一化，后者数组可以被解释成前者数组发生的概率。

因为它涉及到指数计算和对序列长度进行求和计算，执行softmax往往有较高的成本，有时候使得并行化难以执行。

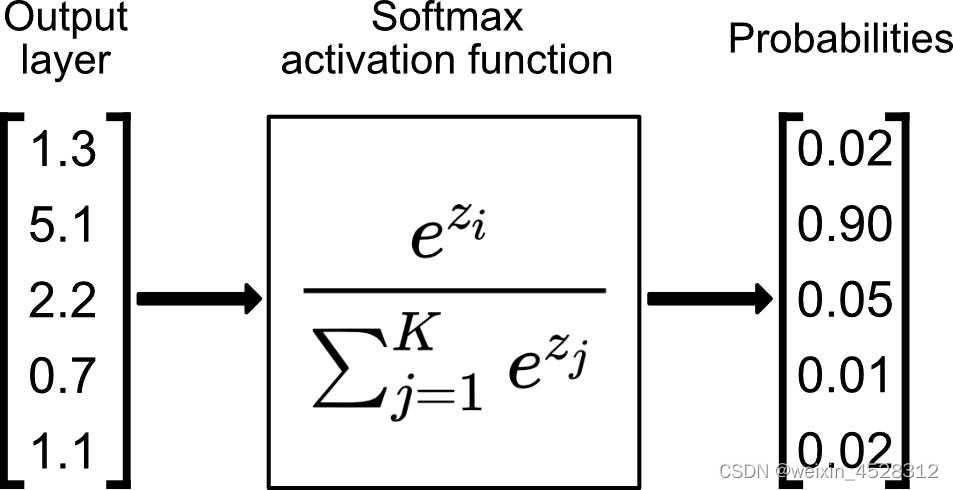
图1，softmax函数的定义和说明

最近，Google DeepMind团队在Arxiv上发表一篇预印本论文，《Replacing softmax with ReLU in Vision Transformers》。该论文发现：利用某种不一定会输出概率分布的新方法，即序列长度归一化的ReLU函数，来替代 softmax 运算，可以使得注意力运算得到可以接近或匹敌传统的 softmax 注意力。这一结果为并行化带来了新方案，因为 ReLU 注意力可以在序列长度维度上并行化，其所需的求和运算少于传统的基于softmax注意力。

图2，谷歌DeepMind新论文

方法和原理

注意力机制：

虽然注意力机制有许多种实现方式，最常用的还是“点积标度注意力”机制。

点积标度注意力机制通过一个两步式流程对一个 d-维的数组 {q_i,k_i,v_i} 进行变换。其中 q, k, v 分别表示查询（query)、键(key)，和值（value）。

第一步，通过下式方程（1）计算注意力矩阵【注：原文作者把下列方程中的 alpha 叫做注意力权重（attention weight）。其实 alpha 并不是注意力训练的权重。权重矩阵（weight matrix，w）是隐含在单个 q, k, v 的向量矩阵中，即 q=w_q*H, k=w_k*H, v=w_v*H。这里 H 是嵌入向量】：

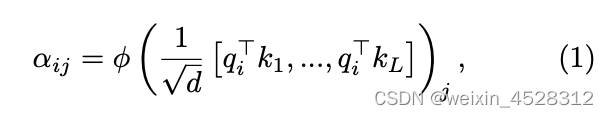
它表示第 i 个 query 向量与第 j 个 key 向量之间的关联程度。其中的 phi 就是通常所说的softmax函数。

第二步，将注意力矩阵与对应的 v 向量相乘，得到第 i 个 query 向量更新后的矩阵，其形式化表示为

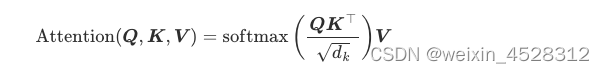
其中 Q, K, V 分别是 query、key、value 向量序列。如果忽略 softmax 激活函数，实际上它就是三个维数为 m x d_k, d_k x n, n x d_v 的矩阵相乘，得到一个维数为 m x d_v 的矩阵，也就是将维数为 m x d_k 的序列 Q 编码成了一个新的维数为 n x d_v 的序列。

这篇论文探索了使用逐点式计算的方案来替代 phi=saftmax函数的可能性。

ReLU注意力机制

在深度学习理论中，ReLU（rectified linear unit，线性整流函数）是指如下‘整流’变换：

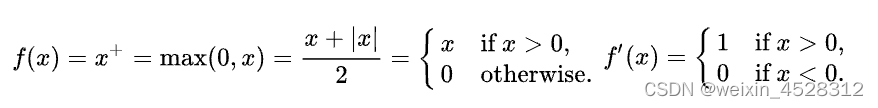
DeepMind团队观察到，可以利用简单的被序列长度 (L) 归一化的线性整流函数，L^(-1)ReLU，替代 softmax，可以产生更加快速有效的结果。他们称这种注意力为 ‘ReLU-attention' （线性整流函数注意力机制）。

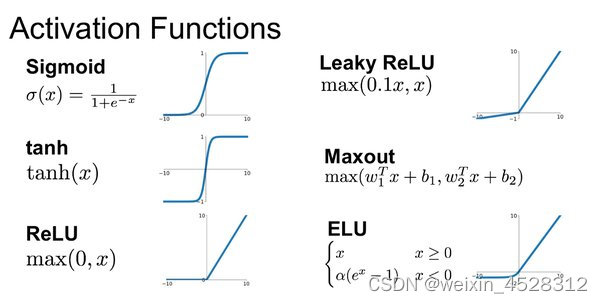
图3，各种不同转换函数的比较。softmax类似于左上的Sigmoid函数；ReLU对应于左下的曲线。

广义上来讲，我们可以定义一大类逐点注意力函数，phi=L^(-a)h，其中 a 在 [0,1] 之间取值，h 可以是 ReLU, ReLU**2, GeLU, softplus, identity, ReLU6 和 sigmoid 中的任何一种函数。

序列长度归一化

因为 Transformer 机制要求所有的注意力矩阵元素在某一指标（j）的求和等于1，这意味着注意力矩阵元素的平均量级应该是~1/L，或者说L^(-1)。其中 L 是序列的长度。因此，在上面方程（1）中的 phi 函数就可以是 phi~L^(-1)ReLU。

本文的结果显示，L^(-1) 的归一化对于模型的训练精度至关重要。然而，在以往类似的工作中，其他研究者并没有注意到这个归一化因子的重要性。

实验与结果

作者在不改变原模型参数的情况下，对BigVision库中的两个程序（ImageNet-21k and ImageNet-1k）进行了测试。作者对这两个模型分别进行了30和300个epoch的训练。

主要结果

图 4 的结果显示出，在 ImageNet-21k 训练方面，ReLU 注意力与 softmax 注意力有着类似的模型训练精度。但是，ReLU 注意力的一大优势是能在序列长度维度上实现并行化，其所需的收集操作比 softmax 注意力更少。

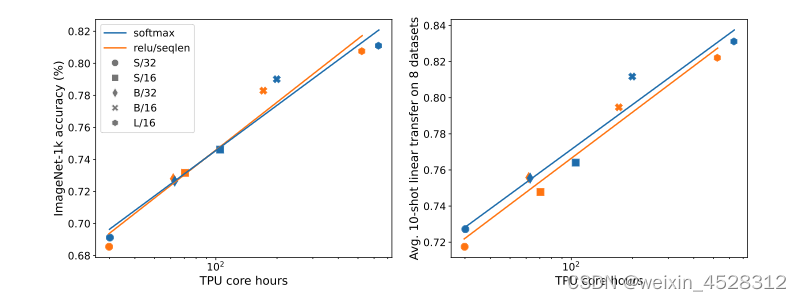
图 4：sofmax注意力和ReLU注意力机制的比较。

序列长度扩展的效果

图 5 对比了序列长度扩展方法与其它多种替代 softmax 的逐点式方案的结果。具体来说，就是用 relu、relu²、gelu、softplus、identity 等方法替代 softmax。X 轴是 α。Y 轴则是 S/32、S/16 和 S/8 视觉 Transformer 模型的准确度。最佳结果通常是在 α 接近 1 时得到。由于没有明确的最佳非线性，所以他们在主要实验中使用了 ReLU，因为它速度更快。

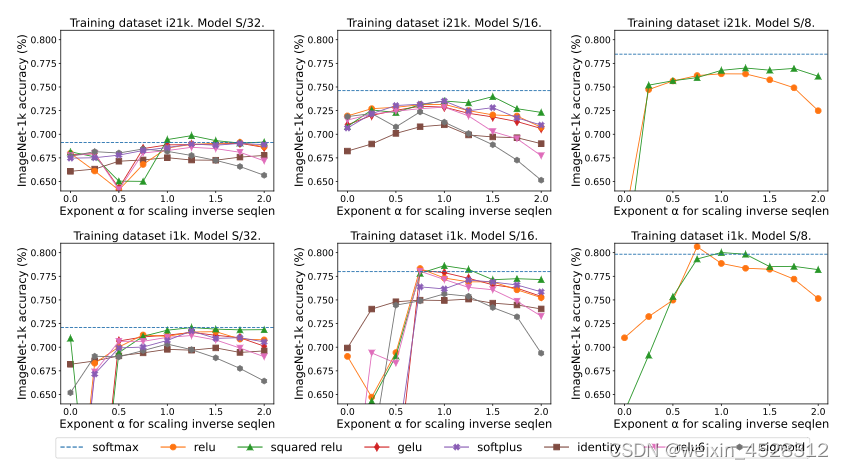
图5：用L^(−α)h 替换 softmax函数，其中 h ∈ {relu, relu2 , gelu, softplus, Identity, relu6, sigmoid},  L 是序列长度。 

qk-layernorm 的效果

此前的研究中，Dehghani等人提出一种叫做qk-归一化的训练机制。在该算法中，q 和 k 矩阵会通过 LayerNorm传递。本文的作者表示，默认使用 qk-layernorm 的原因是在扩展模型大小时有必要防止不稳定情况发生。图 6 展示了移除 qk-layernorm 的影响。这一结果表明 qk-layernorm 对这些模型的影响不大，但当模型规模变大时，情况可能会不一样。

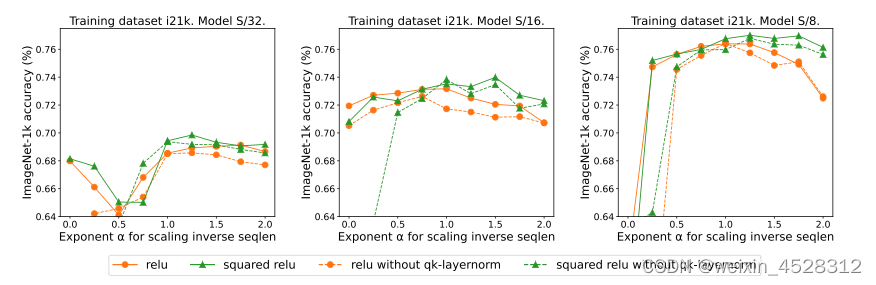
图 6：qk-layernorm对ReLU和ReLU**2的影响。

添加gate的效果

此前也有关于移除 softmax 但是添加一个门控单元（gated unit）的做法，但这种方法无法随序列长度而扩展。具体来说，在门控注意力单元中，会有一个额外的投影产生输出，该输出是在输出投影之前通过矩阵元素相乘得到的。图 7 探究了gate的存在是否可消除对序列长度扩展的需求。总体而言，本文作者观察到，不管有没有gate，通过序列长度扩展都可以得到最佳准确度。也要注意，对于使用 ReLU 的 S/8 模型，这种门控机制会将实验所需的核心时间增多大约 9.3%。

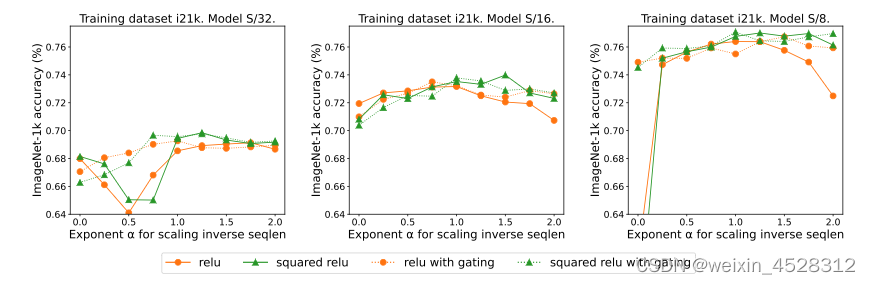
图 4：使用门控注意力单元对 ReLU 和 ReLU**2  注意力机制的影响，其中 L 是序列长度。

小结

Softmax函数是Transformer学习机制的一个核心函数。因为它涉及到指数求和运算，该函数不利于并行化计算。此前曾有研究人员试图利用ReLU或者ReLU**2来取代softmax，但是效果并不理想。

谷歌DeepMind团队的这份研究报告显示，ReLU加上序列长度归一化，可以取得和传统softmax近似的模型训练精度。但是ReLU注意力的速度更快，更有利于并行化运算。

尽管如此，正如作者所指出的，这篇报告留下了许多悬而未决的问题。 特别是，他们不确定为什么这个L^(-1)因子可以提高模型的训练性能，或者这个因子能否通过学习获得。很显然，可能有更好的激活函数等待我们去发现。

参考文献：

M Wortsman, J Lee, J Gilmer, S Kornblith, Google DeepMind, Replacing softmax with ReLU in Vision Transformers. arXiv:2309.08586v1 [cs.CV] 15 Sep 2023. https://arxiv.org/pdf/2309.08586.pdf