习题2-1 分析为什么平方损失函数不适用于分类问题，交叉熵损失函数不适用于回归问题

平方损失函数 平方损失函数（Quadratic Loss Function）经常用在预测标签𝑦为实数值的任务中

表达式为：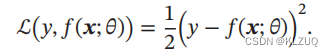

交叉熵损失函数   交叉熵损失函数 （ Cross-Entropy Loss Function） 一般用于分类问题

假设样本的标签 𝑦 ∈ {1, ⋯ , 𝐶} 为离散的类别，模型 𝑓(𝒙; 𝜃) ∈ [0, 1]𝐶 的输出为类别标签的条件概率分布，即

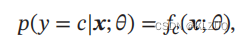
并满足

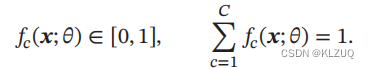
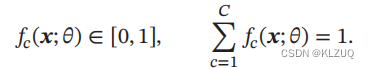
平方损失函数的主要思想是衡量预测值与真实值之间的差距，差距越小，损失越小。这在回归问题中很合适，因为回归问题的目标就是预测一个连续的值。然而，在分类问题中，标签通常是离散的，而不是连续的。比如，在一个二分类问题中，标签只有两种可能的值：“0”和“1”。在这种情况下，使用平方损失函数并不合适，因为它不能很好地处理离散标签。

 交叉熵损失函数用于衡量预测的概率分布与真实的标签分布之间的差距。在分类问题中，这是非常合适的，因为它可以使模型更加关注那些重要的类别。然而，在回归问题中，我们通常希望模型预测一个连续的值，而不是一个概率分布。使用交叉熵损失函数进行回归可能会导致模型过于关注预测的“概率分布”，而忽视了预测的精确值。这可能会导致回归模型的预测结果不如使用平方损失函数准确。

习题 2-12  对于一个三分类问题，数据集的真实标签和模型的预测标签如下：

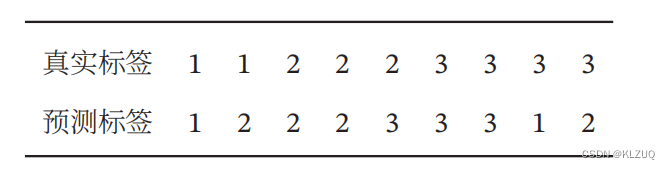
分别计算模型的精确率，回归率，F1值以及它们的宏平均和微平均

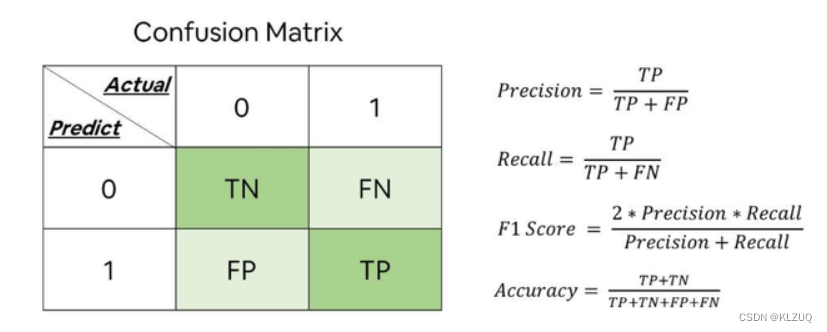
精确率 （ Precision ）， 也叫 精度 或 查准率 ，类别 𝑐 的查准率是所有预测为类别𝑐的样本中预测正确的比例：

样本中预测正确的比例：

宏平均和微平均 为了计算分类算法在所有类别上的总体精确率 、 召回率和 F1

值 ， 经常使用两种平均方法 ， 分别称为 宏平均 （ Macro Average ） 和 微平均 （ Micro Average） [ Yang , 1999 ]

宏平均是 每一类 的性能指标的算术平均值 ：

微平均是 每一个样本 的性能指标的算术平均值．对于单个样本而言，它的精 确率和召回率是相同的（ 要么都是 1 ， 要么都是 0 ）． 因此精确率的微平均和召回率的微平均是相同的． 同理 ， F1 值的微平均指标是相同的 ． 当不同类别的样本数量不均衡时， 使用宏平均会比微平均更合理些 ． 宏平均会更关注小类别上的评价指标

精确率：

召回率：

F值：

宏平均：

微平均：

本期使用公式编辑器：

公式识别 (simpletex.cn)