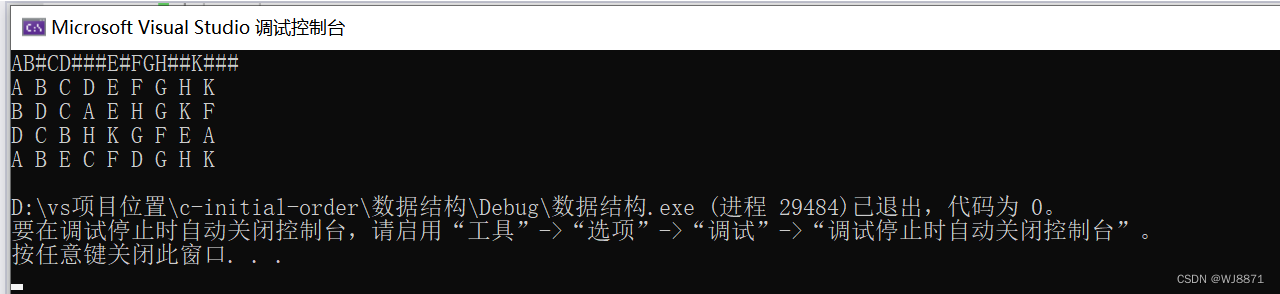
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<malloc.h>
#define N 100
typedef char data_t;

typedef struct tree
{
	data_t data;//存放本节点数据
	struct tree* l_child;//存放左孩子节点地址
	struct tree* r_child;//存放右孩子节点地址
}Tree;

Tree* Create_Tree()
{
	Tree* root;

	char ch;
	scanf("%c", &ch);//通过输入的ch是否为特殊符号来判断该节点是否有孩子节点

	if (ch == '#') {	//不存在孩子节点
		return NULL;
	}
	else {
		root = (Tree*)malloc(sizeof(Tree));
		if (NULL == root) {
			printf("创建失败\n");
			return NULL;
		}

		root->data = ch;
		root->l_child = Create_Tree();//存在左孩子节点，递归调用本函数，使得左孩子节点先被赋值

		root->r_child = Create_Tree();


		return root;
	}
}

void Preorder_Tree(Tree* root)
{
	if (NULL == root) {
		return;
	}

	printf("%c ", root->data);//输出当前节点的数据
	Preorder_Tree(root->l_child);//将子节点作为下一个根节点遍历左孩子数
	Preorder_Tree(root->r_child);//将子节点作为下一个根节点遍历左孩子数
	
}
void Mediate_Tree(Tree* root)
{
	if (NULL == root) {
		return;
	}

	Mediate_Tree(root->l_child);
	printf("%c ", root->data);
	Mediate_Tree(root->r_child);
	
}

void Post_Tree(Tree* root)
{
	if (NULL == root) {
		return;
	}

	Post_Tree(root->l_child);
	Post_Tree(root->r_child);
	printf("%c ", root->data);
	
}

void Level_Tree(Tree* tree)
{
	if (tree == NULL) {
		return;
	}

	Tree* pos[N];
	int front, rear;//队头指针和队尾指针，用于出队和入队操作

	rear = N;
	while (rear--) {
		pos[rear] = NULL;//全部置为空，方便后续判断
	}

	front = rear = 1;//此时为空队列，都指向第一个元素
	pos[front] = tree;
	rear++;//对尾指针偏移一位，用于存放新数据
	while (pos[front] != NULL) {
		printf("%c ", pos[front]->data);
		if (pos[front]->l_child != NULL) {
			pos[rear] = pos[front]->l_child;//左孩子节点入队
			rear++;
		}
		if (pos[front]->r_child != NULL) {
			pos[rear] = pos[front]->r_child;//右孩子节点入队
			rear++;//尾指针偏移
		}
		front++;//头指针偏移一位判断下一个元素		
	}
	
}

int main()
{

	Tree* root=Create_Tree();
	Preorder_Tree(root);
	printf("\n");

	Mediate_Tree(root);
	printf("\n");

	Post_Tree(root);
	printf("\n");

	Level_Tree(root);
	printf("\n");
	return 0;


}

运行结果如下：