反应函数

1 引言

谢老师的《经济博弈论》书中对反应函数并没有给出一般笼统的定义，而是将其应用与古诺模型并给出了相关解释：反应函数是指在无限策略的古诺博弈模型中，博弈方的策略有无限多种，因此各个博弈方的最佳对策也有无限种，它们之间往往构成一种连续函数的关系，把这个连续函数称为反应函数。
有趣的是百度百科对于反应函数的定义与谢老师书上的一致，但是在该词条正文中，还有一句话是：在经济学中，反应函数在博弈论古诺模型中有相应的应用，在假设竞争对手产生了给定产出水平的情况下，反应函数可以得出你的最佳产出水平。
这句话其实比较通俗易懂得解释了反应函数的定义，就是说：反应函数就是当一个企业做经营决策(如产量决策、价格决策等)时，对于给定的其他竞争企业的经营决策，所做出的反应,表明这一反应关系的函数。大白话就是，你做了决策后，我根据你的决策做出我的决策，那描述“根据你的决定，做出我的决定”的关系的函数，称为反应函数。

2 反应函数

根据你的先手，决定对我最有利的后手，是反应函数最关键的地方。我们以前一篇文章的连续产量古诺模型为例：
在上述两寡头古诺模型中,对厂商2的任意产量q2 ,厂商1的最佳对策产量q1，是下面最大化问题的解：
$$\underset{q_1}{\max }{\pi }_1=\underset{q_1}{\max }(-q_1^2-c{q}_1-q_1{q}_2+8q_1)$$
也就是给定$q_2$，求能让厂商1得到最优利润的$q_1$。

令${\pi }_1$对$q_1$求一阶导，并等于0，得到：
$$-2q_1-c-q_2+8=0$$
即：
$$q_1=\frac{8-c-q_2}{2}$$
令：
$$q_1=\frac{8-c-q_2}{2}=R_1(q_2)$$
得到的这个函数$R(q_2)$是对于厂商2的每一个可能产量，厂商1最佳产量的计算公式。这个函数称为厂商1对厂商⒉产量的“反应函数”(reaction function)。
同理,可求出厂商2对厂商1产量$q1$的反应函数为：
$$q_2=\frac{8-c-q_1}{2}=R_2(q_1)$$
显而易见，$R_1(q_2)$、$R_2(q_1)$这两个反应函数都是线性函数(linear function),我们在坐标平面上用两条直线表示出来，更好得进行研究。

3 图像

首先我们分别确定两个线性函数在坐标系上的两点，以数对$(q_1,q_2)$表示。对于$q_1=R_1(q_2)$，其经过$(\frac{8-c}{2},0)$、$(0,8-c)$两点；对于$q_2=R_2(q_1)$，其经过$(8-c,0)$、$(0,\frac{8-c}{2})$两点，如下图所示：

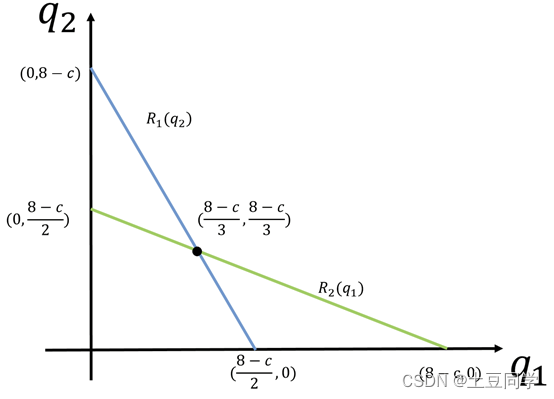
根据图像可以看出:

1. 当一方产量选择为0时,另一方的最佳反应为$\frac{8-c}{2}$,这正是上篇文章中提到的实现市场总利益最大的产量,这时候等于一个厂商垄断市场;
2. 当一方产量达到$8-c$时,另一方被迫生产0,因为后者坚持生产无利可图.

在两个反应函数对应的两条直线上,只有交点$(\frac{8-c}{3},\frac{8-c}{3})$代表的产量组合,才是由相互对对方的最佳反应构成的。
需要注意的是，$q_1=R_1(q_2)$上其他所有点$(q_1,q_2)$代表了只有$q_1$是对$q_2$的最佳反应, $q_2$不是对$q_1$的最佳反应；而$q_2=R_2(q_1)$上其他点代表了只有$q_2$是对$q_1$的最佳反应,$q_1$不是对$q_2$的最佳反应。因此，根据纳什均衡的定义,当$(q_1,q_2)=(\frac{8-c}{3},\frac{8-c}{3})$，即$q_1$、$q_2$相互是对于对方的最佳反应，是该博弈唯一的纳什均衡。这与上篇文章通过数理推导得到的结论一致。

4 结语

得益是策略多元连续函数的博弈,都可以求每个博弈方的反应函数，解出各博弈方反应函数的交点就是纳什均衡。这种用反应函数求纳什均衡的方法,称为“反应函数法”。