两种常见矩形框旋转方法推导及其C++实现

news2025/1/11 2:51:50

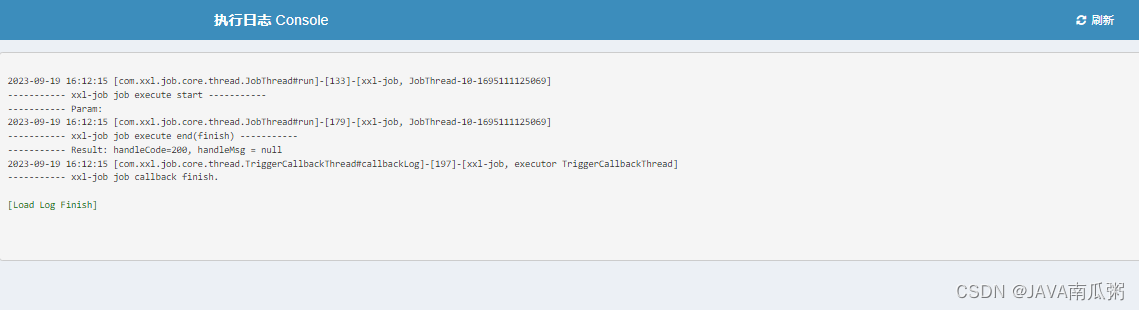
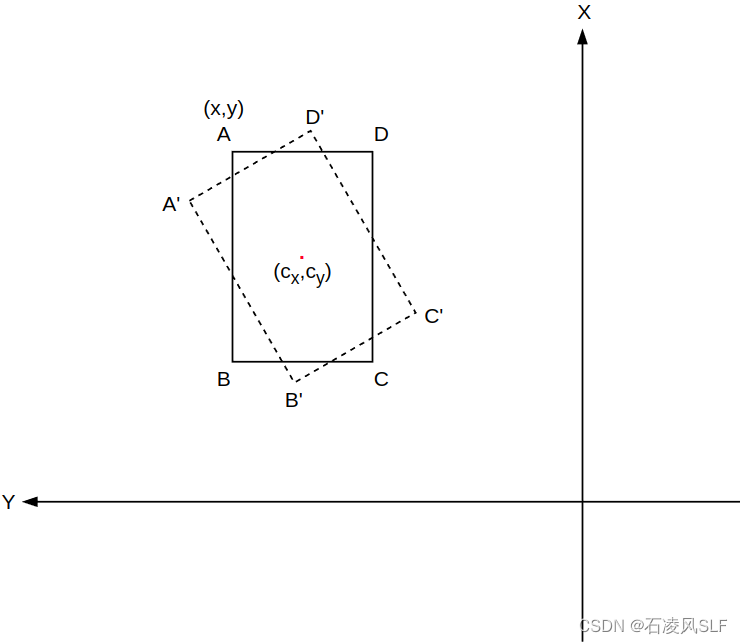
在已知矩形中心点、长宽和旋转角度（定义为矩形最长边与X轴正方向的夹角），如何确定矩形四个顶点的坐标，通常有以下两种处理方法。

法一：直接对顶点进行旋转

比如下图虚线框矩形是实线框矩形绕矩形中心点旋转后得到。在已知矩形中心点坐标和长宽的前提下，实线框四顶点坐标可直接换算得到。然后就是分析计算经旋转后的虚线框矩形的四顶点坐标。

由于是绕矩形中心点旋转，因此可以将坐标系原点平移到矩形中心点位置。然后将矩形框四顶点用极坐标表示，并转换成直角坐标。

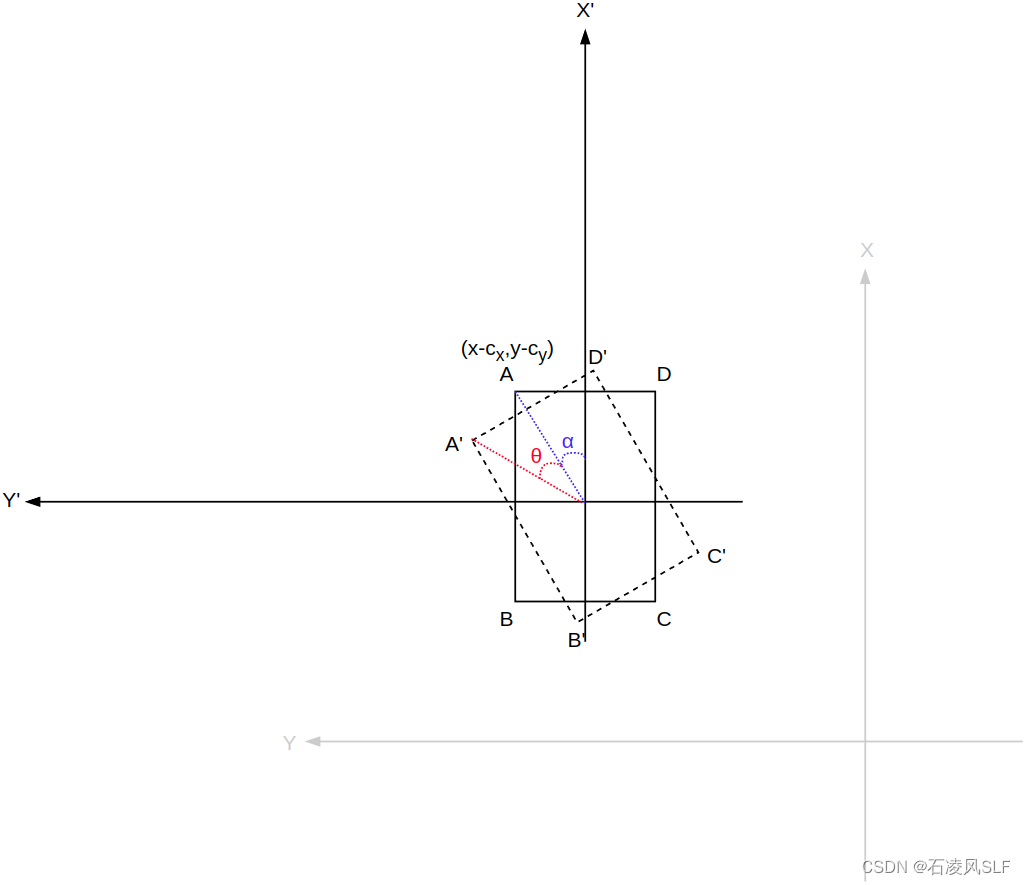
旋转前A顶点坐标：（其中 $r$ 表示矩形框四个顶点距离坐标原点的距离，α表示顶点与坐标原点连线与X轴的夹角）

$A=\left ( r\cdot \cos \alpha ,r\cdot \sin \alpha \right )=\left ( x-c_{x},y-c_{y} \right )$

则绕坐标原点旋转θ角度后A'顶点坐标：

$A'=\left ( r\cdot \cos \left ( \alpha+\theta \right ) ,r\cdot \sin \left ( \alpha+\theta \right ) \right )$

对A'顶点坐标按照三角函数的和差角公式展开：

$A'=\left ( r\cdot \cos \alpha \cdot \cos \theta -r\cdot \sin \alpha \cdot \sin \theta ,r\cdot \sin \alpha \cdot \cos \theta +r\cdot \sin \theta \cdot \cos \alpha \right )$

将A顶点坐标代入A'顶点坐标则有：

$A'=\left ( \left ( x-c_{x} \right ) \cdot \cos \theta -\left ( y-c_{y} \right ) \cdot \sin \theta ,\left ( y-c_{y} \right ) \cdot \cos \theta +\left ( x-c_{x} \right )\cdot \sin \theta \right )$

用矩阵形式表示：

$A'=\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix}\cdot \left ( \begin{bmatrix} x\\ y \end{bmatrix}-\begin{bmatrix} c_{x}\\ c_{y} \end{bmatrix} \right )$

由于坐标系原点被平移到矩形中心点位置，因此最终还需将A'顶点坐标平移回去：

$A'=\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix}\cdot \left ( \begin{bmatrix} x\\ y \end{bmatrix}-\begin{bmatrix} c_{x}\\ c_{y} \end{bmatrix} \right )+\begin{bmatrix} c_{x}\\ c_{y} \end{bmatrix}$

法二：根据三角形几何性质换算顶点坐标

针对四顶点分别绘制出下图所示辅助线，通过相似三角形不难得到下图中两相等辅助角。

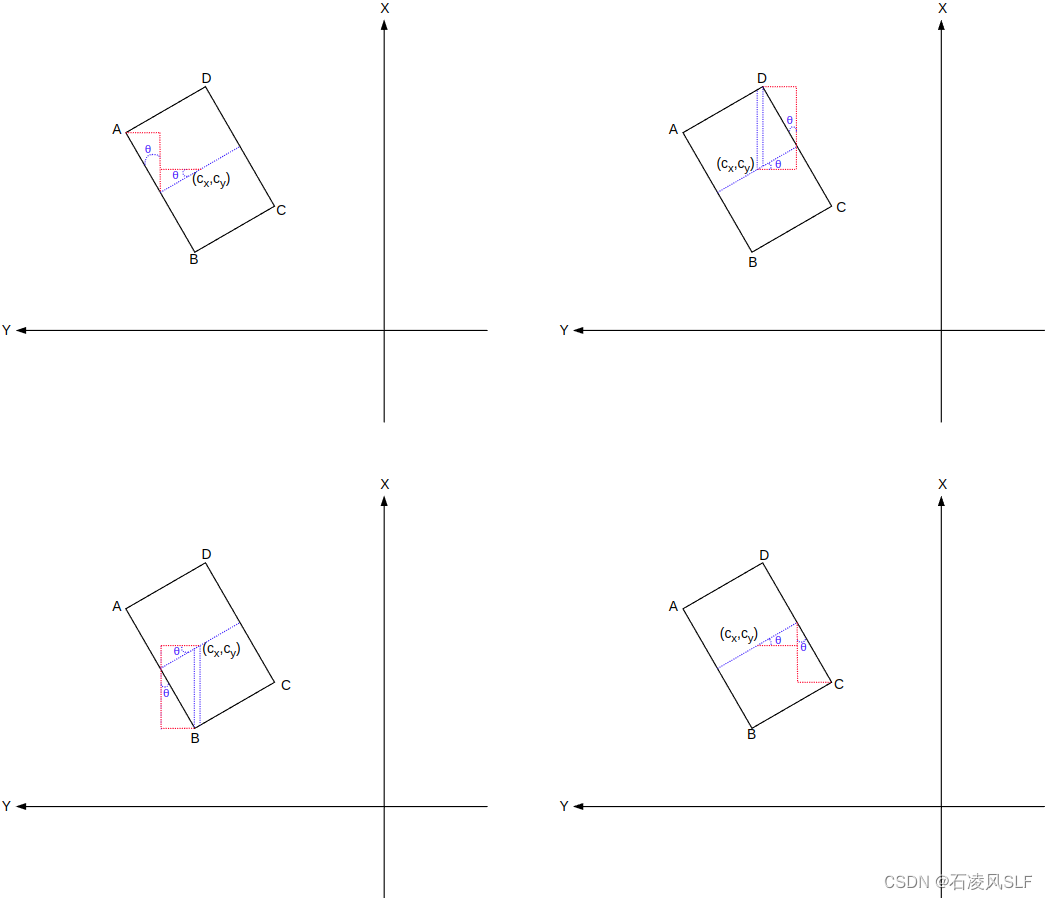
矩形四顶点坐标分别为：

$A:\left\{\begin{matrix} x=c_{x}+\frac{l}{2}\cdot \cos \theta-\frac{w}{2}\cdot \sin \theta \\ y=c_{y}+\frac{l}{2}\cdot \sin \theta+\frac{w}{2}\cdot \cos \theta \end{matrix}\right.$

$B:\left\{\begin{matrix} x=c_{x}-\frac{l}{2}\cdot \cos \theta-\frac{w}{2}\cdot \sin \theta \\ y=c_{y}-\frac{l}{2}\cdot \sin \theta+\frac{w}{2}\cdot \cos \theta \end{matrix}\right.$

$C:\left\{\begin{matrix} x=c_{x}-\frac{l}{2}\cdot \cos \theta+\frac{w}{2}\cdot \sin \theta \\ y=c_{y}-\frac{l}{2}\cdot \sin \theta-\frac{w}{2}\cdot \cos \theta \end{matrix}\right.$

$D:\left\{\begin{matrix} x=c_{x}+\frac{l}{2}\cdot \cos \theta+\frac{w}{2}\cdot \sin \theta \\ y=c_{y}+\frac{l}{2}\cdot \sin \theta-\frac{w}{2}\cdot \cos \theta \end{matrix}\right.$

由于A与C、B与D分别是关于 $\left ( c_{x},c_{y} \right )$ 的对称点，所以各项正负号相反。

C++代码实现

#include <iostream>
#include <cmath>
#include <vector>

// #include <Eigen/Core>
#include <eigen3/Eigen/Core>

#define MATH_PI 3.14159265358979323846264338327950288419716939937510L

template <typename T>
struct Point2D {
  T x = 0;
  T y = 0;
};
typedef Point2D<float> Point2DF;
typedef Point2D<double> Point2DD;

typedef struct {
    Point2DF center;
    float length;
    float width;
    float theta; //rad, (-pi,pi]
} ST_BOX_INFO;

typedef struct {
    Point2DF a;
    Point2DF b;
    Point2DF c;
    Point2DF d;
} ST_BOX_FOUR_VERTICES;

void RotateBoxVerticesMethod1(const ST_BOX_INFO& origin_box, ST_BOX_FOUR_VERTICES& rotated_box);
void RotateBoxVerticesMethod2(const ST_BOX_INFO& origin_box, ST_BOX_FOUR_VERTICES& rotated_box);

int main(void) {
    ST_BOX_INFO origin_box;
    origin_box.center.x = 4;
    origin_box.center.y = 3;
    origin_box.length = 4;
    origin_box.width = 2;
    origin_box.theta = 0.5 * MATH_PI;
    // origin_box.theta = 0.5 * 0.5 * MATH_PI;

    ST_BOX_FOUR_VERTICES rotated_box1, rotated_box2;
    RotateBoxVerticesMethod1(origin_box, rotated_box1);
    RotateBoxVerticesMethod2(origin_box, rotated_box2);

    return 0;
}

void RotateBoxVerticesMethod1(const ST_BOX_INFO& origin_box, ST_BOX_FOUR_VERTICES& rotated_box) {
    Eigen::MatrixXd R = Eigen::MatrixXd::Zero(8, 8);
    Eigen::VectorXd t(8);
    Eigen::VectorXd vertices(8);

    const auto l_half = 0.5 * origin_box.length;
    const auto w_half = 0.5 * origin_box.width;
    auto theta = origin_box.theta;
    if (1.0e-6 > (MATH_PI - std::fabs(theta))) {
        theta = 0.0;
    } else if (1.0e-6 > std::fabs((0.5 * MATH_PI) - std::fabs(theta))) {
        ;
    } else if ((0.5 * MATH_PI) < theta) {
        theta = theta - MATH_PI;
    } else if ((-0.5 * MATH_PI) > theta) {
        theta = theta + MATH_PI;
    }

    rotated_box.a.x = origin_box.center.x + l_half;
    rotated_box.a.y = origin_box.center.y + w_half;
    rotated_box.b.x = origin_box.center.x - l_half;
    rotated_box.b.y = origin_box.center.y + w_half;
    rotated_box.c.x = origin_box.center.x - l_half;
    rotated_box.c.y = origin_box.center.y - w_half;
    rotated_box.d.x = origin_box.center.x + l_half;
    rotated_box.d.y = origin_box.center.y - w_half;
    std::cout << "before rotated: (" << rotated_box.a.x << ',' << rotated_box.a.y << ')'
             << '(' << rotated_box.b.x << ',' << rotated_box.b.y << ')'
             << '(' << rotated_box.c.x << ',' << rotated_box.c.y << ')'
             << '(' << rotated_box.d.x << ',' << rotated_box.d.y << ')' << std::endl;

    R(0, 0) = R(1, 1) = R(2, 2) = R(3, 3) = R(4, 4) = R(5, 5) = R(6, 6) = R(7, 7) = std::cos(theta);
    R(1, 0) = R(3, 2) = R(5, 4) = R(7, 6) = std::sin(theta);
    R(0, 1) = R(2, 3) = R(4, 5) = R(6, 7) = -R(1, 0);

    t << origin_box.center.x, origin_box.center.y, origin_box.center.x, origin_box.center.y,
        origin_box.center.x, origin_box.center.y, origin_box.center.x, origin_box.center.y;

    vertices << rotated_box.a.x, rotated_box.a.y,
                rotated_box.b.x, rotated_box.b.y,
                rotated_box.c.x, rotated_box.c.y,
                rotated_box.d.x, rotated_box.d.y;

    const Eigen::VectorXd rslt = R * (vertices - t) + t;

    rotated_box.a.x = rslt(0);
    rotated_box.a.y = rslt(1);
    rotated_box.b.x = rslt(2);
    rotated_box.b.y = rslt(3);
    rotated_box.c.x = rslt(4);
    rotated_box.c.y = rslt(5);
    rotated_box.d.x = rslt(6);
    rotated_box.d.y = rslt(7);
    std::cout << "after rotated: (" << rotated_box.a.x << ',' << rotated_box.a.y << ')'
             << '(' << rotated_box.b.x << ',' << rotated_box.b.y << ')'
             << '(' << rotated_box.c.x << ',' << rotated_box.c.y << ')'
             << '(' << rotated_box.d.x << ',' << rotated_box.d.y << ')' << std::endl;
}

void RotateBoxVerticesMethod2(const ST_BOX_INFO& origin_box, ST_BOX_FOUR_VERTICES& rotated_box) {
    auto theta = origin_box.theta;
    if (1.0e-6 > (MATH_PI - std::fabs(theta))) {
        theta = 0.0;
    } else if (1.0e-6 > std::fabs((0.5 * MATH_PI) - std::fabs(theta))) {
        ;
    } else if ((0.5 * MATH_PI) < theta) {
        theta = theta - MATH_PI;
    } else if ((-0.5 * MATH_PI) > theta) {
        theta = theta + MATH_PI;
    }

    Eigen::Vector2d direction(std::cos(theta), std::sin(theta));
    Eigen::Vector2d orthog_dir(-direction.y(), direction.x());
    Eigen::Vector2d delta_x = 0.5 * origin_box.length * direction;
    Eigen::Vector2d delta_y = 0.5 * origin_box.width * orthog_dir;
    Eigen::Vector2d center = Eigen::Vector2d(origin_box.center.x, origin_box.center.y);
    std::vector<Eigen::Vector2d> vertices(4);
    vertices[0] = center + (delta_x + delta_y);
    vertices[1] = center + (-delta_x + delta_y);
    vertices[2] = center + (-delta_x - delta_y);
    vertices[3] = center + (delta_x - delta_y);
    
    rotated_box.a.x = vertices[0](0);
    rotated_box.a.y = vertices[0](1);
    rotated_box.b.x = vertices[1](0);
    rotated_box.b.y = vertices[1](1);
    rotated_box.c.x = vertices[2](0);
    rotated_box.c.y = vertices[2](1);
    rotated_box.d.x = vertices[3](0);
    rotated_box.d.y = vertices[3](1);
    std::cout << "after rotated: (" << rotated_box.a.x << ',' << rotated_box.a.y << ')'
             << '(' << rotated_box.b.x << ',' << rotated_box.b.y << ')'
             << '(' << rotated_box.c.x << ',' << rotated_box.c.y << ')'
             << '(' << rotated_box.d.x << ',' << rotated_box.d.y << ')' << std::endl;
}

若是要计算三维长方体的的八个顶点（已知中心点、长宽高和旋转角度，且pitch、roll角恒为0°），则用以上同样的方法先计算底部长方形的四顶点坐标，然后再将长方体的高累加到四顶点坐标对应轴上，即可得到顶部长方形四顶点的坐标。

其它方法可在评论区留言补充。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1037619.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！