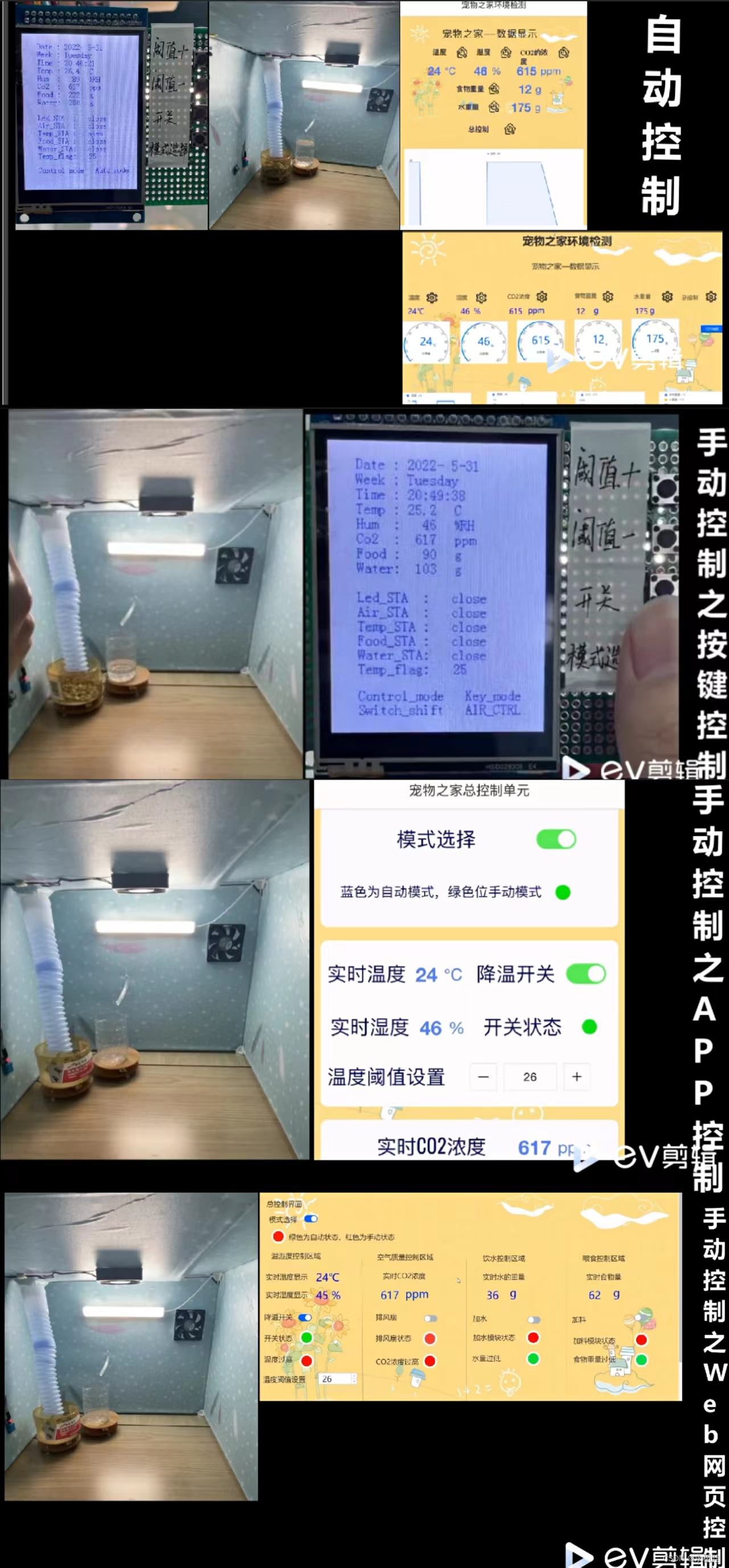
题目
T(T<=10)组样例,每次给出一个n(2<=n<=1e18),
询问多少对,满足
答案对998244353取模,保证n-1不是998244353倍数
思路来源
OEIS、SSerxhs、官方题解
2023 ICPC 网络赛 第一场简要题解 - 知乎
题解
官方题解还没有补,OEIS打了个表然后就通过了
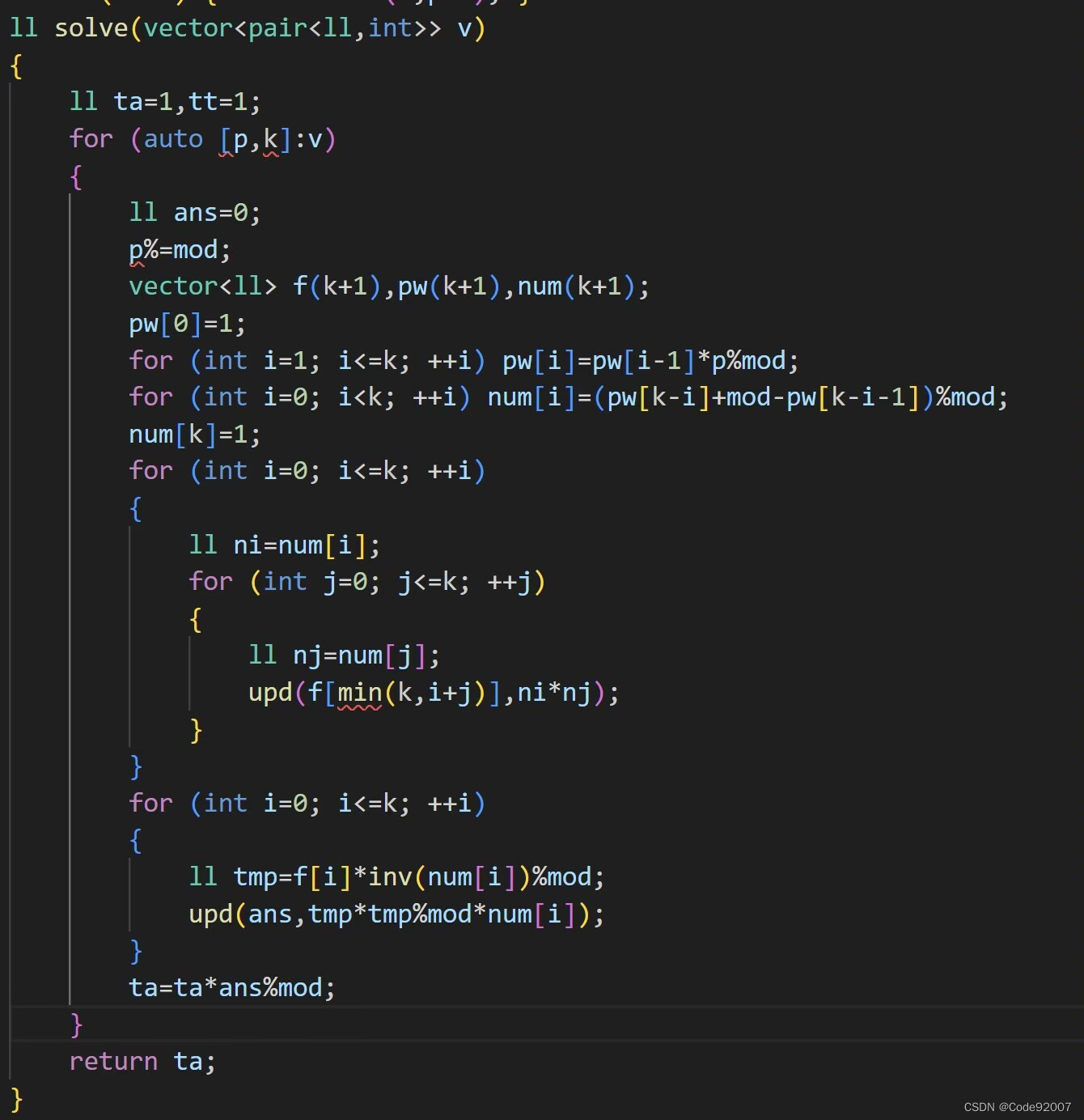
这里给一下SSerxhs教的做法吧(图源:我、tanao学弟)
SSerxhs代码
我的理解
首先,证一下这个和是等价的,其中bi为满足
的(x,y)的对数
关于这部分,题解里给的中国剩余定理的构造,也很巧妙

剩下的部分就很神奇了,首先需要注意到各个素因子的贡献是独立的,可以连积

对于求某个素因子的幂次的贡献时,用到了解的分布是均匀的性质

代码1(OEIS)
#include<bits/stdc++.h>
using namespace std;
#define In inline
typedef long long ll;
typedef double db;
const int INF = 0x3f3f3f3f;
const db eps = 1e-8;
map<ll,ll>ans;
inline ll read()
{
ll ans = 0;
char ch = getchar(), last = ' ';
while(!isdigit(ch)) {last = ch; ch = getchar();}
while(isdigit(ch)) {ans = (ans << 1) + (ans << 3) + ch - '0'; ch = getchar();}
if(last == '-') ans = -ans;
return ans;
}
inline void write(ll x)
{
if(x < 0) x = -x, putchar('-');
if(x >= 10) write(x / 10);
putchar(x % 10 + '0');
}
ll n;
In ll mul(ll a, ll b, ll mod)
{
ll d = (long double)a / mod * b + 1e-8;
ll r = a * b - d * mod;
return r < 0 ? r + mod : r;
}
In ll quickpow(ll a, ll b, ll mod)
{
ll ret = 1;
for(; b; b >>= 1, a = mul(a, a, mod))
if(b & 1) ret = mul(ret, a, mod);
return ret;
}
In bool test(ll a, ll d, ll n)
{
ll t = quickpow(a, d, n);
if(t == 1) return 1;
while(d != n - 1 && t != n - 1 && t != 1) t = mul(t, t, n), d <<= 1;
return t == n - 1;
}
int a[] = {2, 3, 5, 7, 11};
In bool miller_rabin(ll n)
{
if(n == 1) return 0;
for(int i = 0; i < 5; ++i)
{
if(n == a[i]) return 1;
if(!(n % a[i])) return 0;
}
ll d = n - 1;
while(!(d & 1)) d >>= 1;
for(int i = 1; i <= 5; ++i)
{
ll a = rand() % (n - 2) + 2;
if(!test(a, d, n)) return 0;
}
return 1;
}
In ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
In ll f(ll x, ll a, ll mod) {return (mul(x, x, mod) + a) % mod;}
const int M = (1 << 7) - 1;
ll pollard_rho(ll n)
{
for(int i = 0; i < 5; ++i) if(n % a[i] == 0) return a[i];
ll x = rand(), y = x, t = 1, a = rand() % (n - 2) + 2;
for(int k = 2;; k <<= 1, y = x)
{
ll q = 1;
for(int i = 1; i <= k; ++i)
{
x = f(x, a, n);
q = mul(q, abs(x - y), n);
if(!(i & M))
{
t = gcd(q, n);
if(t > 1) break;
}
}
if(t > 1 || (t = gcd(q, n)) > 1) break;
}
return t;
}
In void find(ll x)
{
if(x == 1 ) return;
if(miller_rabin(x)) {ans[x]++;return;}
ll p = x;
while(p == x) p = pollard_rho(x);
while(x % p == 0) x/=p;
find(p); find(x);
}
const ll mod=998244353;
ll modpow(ll x,ll n){
x%=mod;
if(!x)return 0;
ll res=1;
for(;n;n>>=1,x=1ll*x*x%mod){
if(n&1)res=1ll*res*x%mod;
}
return res;
}
ll cal(ll p,ll e){
//printf("p:%lld e:%lld\n",p,e);
return (modpow(p,e+1)+modpow(p,e)-1+mod)%mod*modpow(p,2*e-1)%mod;
}
int main()
{
srand(time(0));
int T = read();
while(T--)
{
ans.clear();
n = read();
ll m=n-1;
find(m);
ll phi=m%mod,res=1;
for(auto &v:ans){
ll p=v.first,e=0;
while(m%p==0)m/=p,e++;
res=res*cal(p,e)%mod;
}
res=(res+phi*phi%mod)%mod;
printf("%lld\n",res);
}
return 0;
}代码2(SSerxhs代码)
#include<bits/stdc++.h>
using namespace std;
#define In inline
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
const int INF = 0x3f3f3f3f;
const db eps = 1e-8;
map<ll,int>ans;
vector<P>ans2;
inline ll read()
{
ll ans = 0;
char ch = getchar(), last = ' ';
while(!isdigit(ch)) {last = ch; ch = getchar();}
while(isdigit(ch)) {ans = (ans << 1) + (ans << 3) + ch - '0'; ch = getchar();}
if(last == '-') ans = -ans;
return ans;
}
inline void write(ll x)
{
if(x < 0) x = -x, putchar('-');
if(x >= 10) write(x / 10);
putchar(x % 10 + '0');
}
ll n;
In ll mul(ll a, ll b, ll mod)
{
ll d = (long double)a / mod * b + 1e-8;
ll r = a * b - d * mod;
return r < 0 ? r + mod : r;
}
In ll quickpow(ll a, ll b, ll mod)
{
ll ret = 1;
for(; b; b >>= 1, a = mul(a, a, mod))
if(b & 1) ret = mul(ret, a, mod);
return ret;
}
In bool test(ll a, ll d, ll n)
{
ll t = quickpow(a, d, n);
if(t == 1) return 1;
while(d != n - 1 && t != n - 1 && t != 1) t = mul(t, t, n), d <<= 1;
return t == n - 1;
}
int a[] = {2, 3, 5, 7, 11};
In bool miller_rabin(ll n)
{
if(n == 1) return 0;
for(int i = 0; i < 5; ++i)
{
if(n == a[i]) return 1;
if(!(n % a[i])) return 0;
}
ll d = n - 1;
while(!(d & 1)) d >>= 1;
for(int i = 1; i <= 5; ++i)
{
ll a = rand() % (n - 2) + 2;
if(!test(a, d, n)) return 0;
}
return 1;
}
In ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
In ll f(ll x, ll a, ll mod) {return (mul(x, x, mod) + a) % mod;}
const int M = (1 << 7) - 1;
ll pollard_rho(ll n)
{
for(int i = 0; i < 5; ++i) if(n % a[i] == 0) return a[i];
ll x = rand(), y = x, t = 1, a = rand() % (n - 2) + 2;
for(int k = 2;; k <<= 1, y = x)
{
ll q = 1;
for(int i = 1; i <= k; ++i)
{
x = f(x, a, n);
q = mul(q, abs(x - y), n);
if(!(i & M))
{
t = gcd(q, n);
if(t > 1) break;
}
}
if(t > 1 || (t = gcd(q, n)) > 1) break;
}
return t;
}
In void find(ll x)
{
if(x == 1 ) return;
if(miller_rabin(x)) {ans[x]++;return;}
ll p = x;
while(p == x) p = pollard_rho(x);
while(x % p == 0) x/=p;
find(p); find(x);
}
const ll mod=998244353;
ll modpow(ll x,ll n){
x%=mod;
if(!x)return 0;
ll res=1;
for(;n;n>>=1,x=1ll*x*x%mod){
if(n&1)res=1ll*res*x%mod;
}
return res;
}
ll cal(ll p,ll e){
//printf("p:%lld e:%lld\n",p,e);
return (modpow(p,e+1)+modpow(p,e)-1+mod)%mod*modpow(p,2*e-1)%mod;
}
ll sol(){
ll ta=1;//tt=1;
for(auto &x:ans2){
ll p=x.first,ans=0;
int k=x.second;
p%=mod;
vector<ll> f(k+1),pw(k+1),num(k+1);
pw[0]=1;
rep(i,1,k)pw[i]=pw[i-1]*p%mod;
rep(i,0,k-1)num[i]=(pw[k-i]+mod-pw[k-i-1])%mod;
num[k]=1;
rep(i,0,k){
ll ni=num[i];
rep(j,0,k){
ll nj=num[j];
f[min(k,i+j)]=(f[min(k,i+j)]+ni*nj%mod)%mod;
}
}
rep(i,0,k){
ll tmp=f[i]*modpow(num[i],mod-2)%mod;
ans=(ans+tmp*tmp%mod*num[i]%mod)%mod;
}
ta=ta*ans%mod;
}
return ta;
}
int main()
{
srand(time(0));
int T = read();
while(T--)
{
ans.clear();
ans2.clear();
n = read();
ll m=n-1;
find(m);
//ll phi=m%mod,res=1;
for(auto &v:ans){
ll p=v.first,e=0;
while(m%p==0)m/=p,e++;
ans2.push_back(P(p,e));
//res=res*cal(p,e)%mod;
}
m=(n-1)%mod;
ll res=sol();
res=(res+m*m%mod)%mod;
printf("%lld\n",res);
//res=(res+phi*phi%mod)%mod;
//printf("%lld\n",res);
}
return 0;
}