什么树
树是 n(n>=0)个有限集。n=0是空树,在n>1的非空树中有且仅有一个根节点作为树根,其他结构分散在根节点下形成一个个子树。各个子树互不相交。在实际的编码环节中,我们可以用链表和数组来模拟树结构。
为什么需要树结构
我们知道数组结构查询速度快,但增删慢;链表结构增删快,但查询慢。那么,有没有一种数据结构可以两者兼得,在查询快的基础上增删也快呢。答案是 >> 树结构。
什么是二叉树
二叉树是一种特殊的树结构,换句话说就是在普通树转换而来。定义为:二叉树只有一个根节点,二叉树子树都只有两个节点,必须满足左节点小于父节点,右节点大于父节点,而且子节点左边最大值不能大于该节点,子节点右边的最小值不能小于该节点。
为什么要研究二叉树
因为很多实际问题抽象出来就是二叉树的形式,而且普通树很容易抓换成二叉树;另一方面二叉树的数据结构和算法都较为简单,非常便于我们用于实际模拟树结构。
二叉树的存储方式
1、顺序储存
一般用数组模拟顺序储存,用数组下标来区分父子节点层级关系。
二叉树索引满足规定:
父索引 = (子索引 -1)/2
左子索引 = 2父索引+1
右子索引 = 2父索引+2
2、链式储存
一般用链表标识,链表每个节点中包含当前节点数据、左子节点、右子节点、有些还包含是否删除标识。为什么有些包含是否删除标识,因为二叉树链表的删除非常复杂。如果涉及到被删除节点有两个子节点就需要用右子节点或者右子节点最左节点进行替换,该操作还是有些复杂。
删除节点如果存在左右子节点的情况:

小试牛刀
我们用链表来模拟二叉树数据结构
1、创建二叉树工具类提供增删查中序打印方法
/**
* 二叉树
* @author senfel
* @version 1.0
* @date 2022/12/20 11:15
*/
@Data
@Slf4j
public class BinaryTree {
@Data
private class Node{
/**
* 数据
*/
private int key;
/**
* 左节点
*/
private Node leftNode;
/**
* 右节点
*/
private Node rightNode;
public Node() {
}
public Node(int key, Node leftNode, Node rightNode) {
this.key = key;
this.leftNode = leftNode;
this.rightNode = rightNode;
}
}
/**
* 根节点
*/
private Node root;
/**
* 查找
* @param key
* @author senfel
* @date 2022/12/20 11:20
* @return com.example.datademo.data.BinaryTree.Node
*/
public Node find(int key){
Node current = root;
while (current != null){
if(key < current.getKey()){
current = current.getLeftNode();
}else if(key > current.getKey()){
current = current.getRightNode();
}else{
return current;
}
}
return null;
}
/**
* 新增
* @param key
* @author senfel
* @date 2022/12/20 11:27
* @return java.lang.Boolean
*/
public Boolean add(int key){
//封装node
Node node = new Node(key, null, null);
//插入节点
if(Objects.isNull(root)){
root = node;
}else{
Node current = root;
Node parentNode = null;
while (current != null){
if(key > current.getKey()){
//当前值大于节点值 找右子节点
parentNode = current;
current = current.getRightNode();
if(Objects.isNull(current)){
//右子节点不存在,直接写入
parentNode.rightNode = node;
return true;
}
}else if(key < current.getKey()) {
//当前值小于节点值 找左子节点
parentNode = current;
current = current.getLeftNode();
if (Objects.isNull(current)) {
//左子节点为空 直接写入
parentNode.leftNode = node;
return true;
}
}else {
//当前值等于当前节点不插入直接默认返回true
return true;
}
}
}
return false;
}
/**
* 删除节点
* @param key
* @author senfel
* @date 2022/12/20 13:49
* @return java.lang.Boolean
*/
public Boolean delete(int key){
//找到需要删除的节点
Node waitNode = root;
Node parentNode = root;
Boolean isLeftNode = false;
while (waitNode != null && waitNode.getKey() != key){
if(key > waitNode.getKey()){
//被删除数据大于当前节点 取右子节点
isLeftNode = false;
parentNode = waitNode;
waitNode = waitNode.getRightNode();
}else if(key < waitNode.getKey()){
//被删除数据小于当前节点 取左子节点
isLeftNode = true;
parentNode = waitNode;
waitNode = waitNode.getLeftNode();
}
if(Objects.isNull(waitNode)){
return false;
}
}
//如果当前节点没有左右子节点 直接删除即可
if(waitNode.getLeftNode() == null && waitNode.getRightNode() == null){
if(waitNode == root){
//被删除节点就是根节点 根节点直接制空
this.root = null;
return true;
}
if(isLeftNode){
//被删除节点是父节点的左子节点 将父节点左子节点置空即可
parentNode.setLeftNode(null);
return true;
}else{
//将父节点右子节点置空即可
parentNode.setRightNode(null);
}
}else if(waitNode.getLeftNode() != null && waitNode.getRightNode() == null){
//左子节点不为空 右子节点为空
if(waitNode == root){
//被删除节点就是根节点 将被删除节点左子节点放在根节点位置
this.root = parentNode.getLeftNode();
return true;
}
if(isLeftNode){
//被删除节点是父节点的左子节点
parentNode.setLeftNode(waitNode.getLeftNode());
return true;
}else{
parentNode.setRightNode(waitNode.getLeftNode());
return true;
}
}else if(waitNode.getLeftNode() == null && waitNode.getRightNode() != null){
//被删除节点左节点为空 右节点不为空
if(waitNode == root){
//将右节点升级为根节点
this.root = waitNode.getRightNode();
return true;
}
if(isLeftNode){
//被删除节点是父节点的左节点 将节点的右节点升级为父节点左节点
parentNode.setLeftNode(waitNode.getRightNode());
return true;
}else{
parentNode.setRightNode(waitNode.getRightNode());
return true;
}
}else{
//左右子节点都不为空
//1、先要获取替换节点,一般为被删除节点右节点,如果该节点存在左子节点则需要找到最小的左子节点
Node updateNode = getUpdateNode(waitNode);
if(updateNode == null){
return false;
}
if(waitNode == root){
this.root = updateNode;
updateNode.setLeftNode(waitNode.getLeftNode());
return true;
}
if(isLeftNode){
parentNode.setLeftNode(updateNode);
updateNode.setLeftNode(waitNode.getLeftNode());
return true;
}else{
parentNode.setRightNode(updateNode);
updateNode.setLeftNode(waitNode.getLeftNode());
return true;
}
}
return false;
}
/**
* 获取替换节点
* @param waitNode
* @author senfel
* @date 2022/12/20 14:15
* @return Node
*/
private Node getUpdateNode(Node waitNode) {
if(waitNode == null){
return null;
}
Node parentNode = waitNode;
Node updateNode = waitNode;
Node current = waitNode.getRightNode();
while (current != null){
parentNode = updateNode;
updateNode = current;
current = current.getLeftNode();
}
if(updateNode != waitNode.getRightNode()){
//被替换节点不是右子节点需要移动位置
//1、将被替换节点的右节点放置在其父节点的左节点上
parentNode.setLeftNode(updateNode.getRightNode());
//2、将被替换节点的右节点重置为被删除节点的右节点
updateNode.setRightNode(waitNode.getRightNode());
}
return updateNode;
}
/**
* 中序打印二叉树数据
* @param node
* @author senfel
* @date 2022/12/20 15:31
* @return void
*/
public void centerRead(Node node,StringBuffer str){
if(node != null){
centerRead(node.getLeftNode(),str);
str.append(node.getKey()+" ");
centerRead(node.getRightNode(),str);
}
}
}
2、提供测试方法
public static void main(String[] args) {
BinaryTree binaryTree = new BinaryTree();
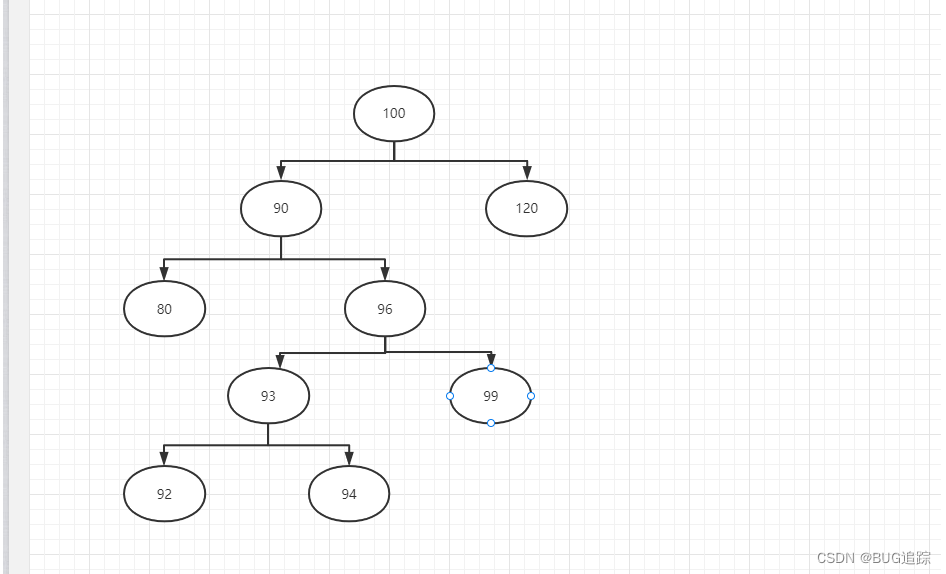
binaryTree.add(100);
binaryTree.add(90);
binaryTree.add(120);
binaryTree.add(80);
binaryTree.add(96);
binaryTree.add(93);
binaryTree.add(99);
binaryTree.add(92);
binaryTree.add(94);
StringBuffer str = new StringBuffer();
binaryTree.centerRead(binaryTree.root,str);
log.error("\n二叉树插入数据后的中序获取结构为:"+str.toString());
binaryTree.delete(90);
str = new StringBuffer();
binaryTree.centerRead(binaryTree.root,str);
log.error("\n二叉树删除90元素数据后的中序获取结构为:"+str.toString());
}
3、查看测试结果
二叉树插入数据后的中序获取结构为:80 90 92 93 94 96 99 100 120
二叉树删除90元素数据后的中序获取结构为:80 92 93 94 96 99 100 120