代码随想录
什么是贪心
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
这么说有点抽象,来举一个例子:
例如,有一堆钞票,你可以拿走十张,如果想达到最大的金额,你要怎么拿?
指定每次拿最大的,最终结果就是拿走最大数额的钱。
每次拿最大的就是局部最优,最后拿走最大数额的钱就是推出全局最优。
再举一个例子如果是 有一堆盒子,你有一个背包体积为n,如何把背包尽可能装满,如果还每次选最大的盒子,就不行了。这时候就需要动态规划。动态规划的问题在下一个系列会详细讲解。
什么时候用贪心
贪心算法、动态规划、机器学习都属于优化算法。当题目要求最优解的时候基本上都是贪心算法或者动态规划
贪心算法并没有固定的套路。
所以唯一的难点就是如何通过局部最优,推出整体最优。
那么如何能看出局部最优是否能推出整体最优呢?有没有什么固定策略或者套路呢?
不好意思,也没有! 靠自己手动模拟,如果模拟可行,就可以试一试贪心策略,如果不可行,可能需要动态规划。
有同学问了如何验证可不可以用贪心算法呢?
最好用的策略就是举反例,如果想不到反例,那么就试一试贪心吧。
可有有同学认为手动模拟,举例子得出的结论不靠谱,想要严格的数学证明。
一般数学证明有如下两种方法:
- 数学归纳法
- 反证法
看教课书上讲解贪心可以是一堆公式,估计大家连看都不想看,所以数学证明就不在我要讲解的范围内了,大家感兴趣可以自行查找资料。
面试中基本不会让面试者现场证明贪心的合理性,代码写出来跑过测试用例即可,或者自己能自圆其说理由就行了。
举一个不太恰当的例子:我要用一下1+1 = 2,但我要先证明1+1 为什么等于2。严谨是严谨了,但没必要。
虽然这个例子很极端,但可以表达这么个意思:刷题或者面试的时候,手动模拟一下感觉可以局部最优推出整体最优,而且想不到反例,那么就试一试贪心。
贪心一般解题步骤
贪心算法一般分为如下四步:
- 将问题分解为若干个子问题
- 找出适合的贪心策略
- 求解每一个子问题的最优解
- 将局部最优解堆叠成全局最优解
这个四步其实过于理论化了,我们平时在做贪心类的题目 很难去按照这四步去思考,真是有点“鸡肋”。
做题的时候,只要想清楚 局部最优 是什么,如果推导出全局最优,其实就够了。
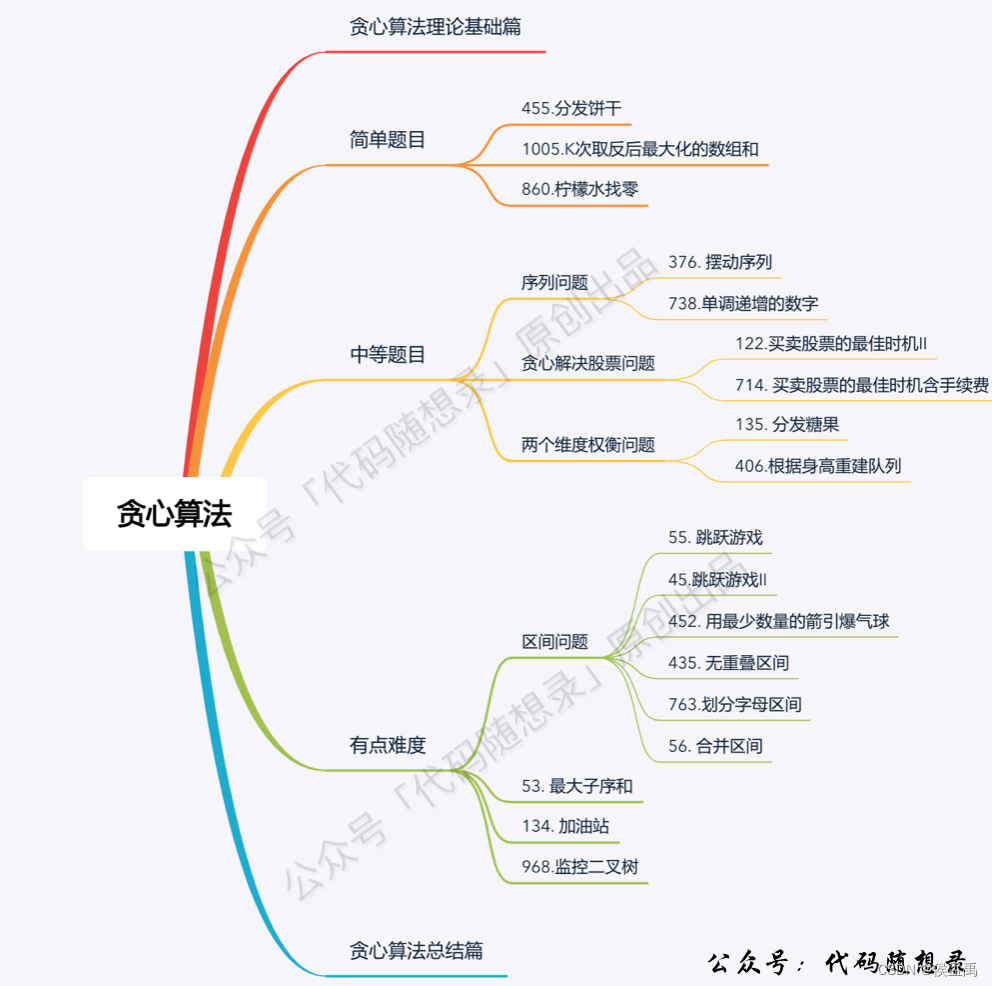
题目
455.分发饼干
455. 分发饼干_侯孟禹的博客-CSDN博客
53. 最大子序和
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
思路:1.因为求最大和,第一个数就是正数才能成为优解,所以当第一个数是负数的时候就跳过
2.求和时,一旦当前和为负数则直接放弃(新加上的数肯定是负数),从下一个数作为第一个数重新开始。
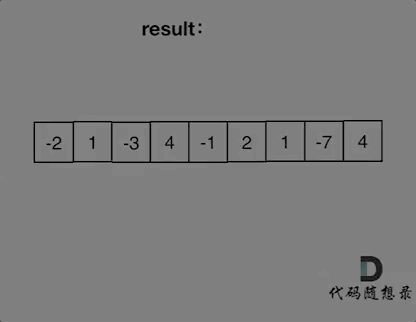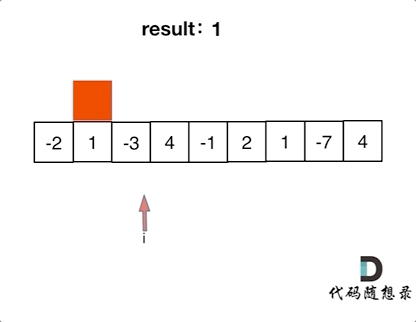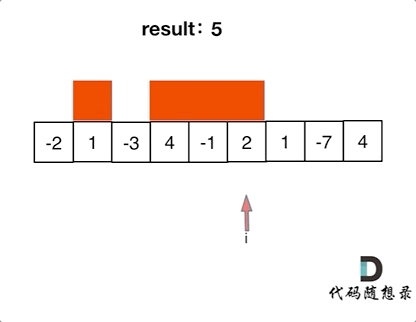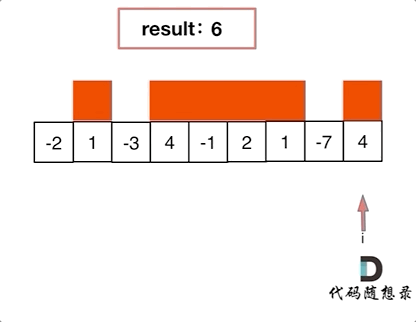
代码:
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int result = INT32_MIN;//不能设成0,否则序列[-1]会返回空,正确返回-1
int count = 0;
for (int i = 0; i < nums.size(); i++) {
count += nums[i];
if (count > result) { // 取区间累计的最大值(相当于不断确定最大子序终止位置)
result = count;
}
//这一句保证第一个数为正;同时也保证当前和为负时从下一个元素重新开始
if (count <= 0) count = 0; // 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和
}
return result;
}
};本题动态规划解法:代码随想录
122.买卖股票的最佳时机 II
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
思路:
如果想到其实最终利润是可以分解的,那么本题就很容易了!
如何分解呢?
假如第 0 天买入,第 3 天卖出,那么利润为:prices[3] - prices[0]。
相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。
此时就是把利润分解为每天为单位的维度,而不是从 0 天到第 3 天整体去考虑!
那么根据 prices 可以得到每天的利润序列:(prices[i] - prices[i - 1]).....(prices[1] - prices[0])。
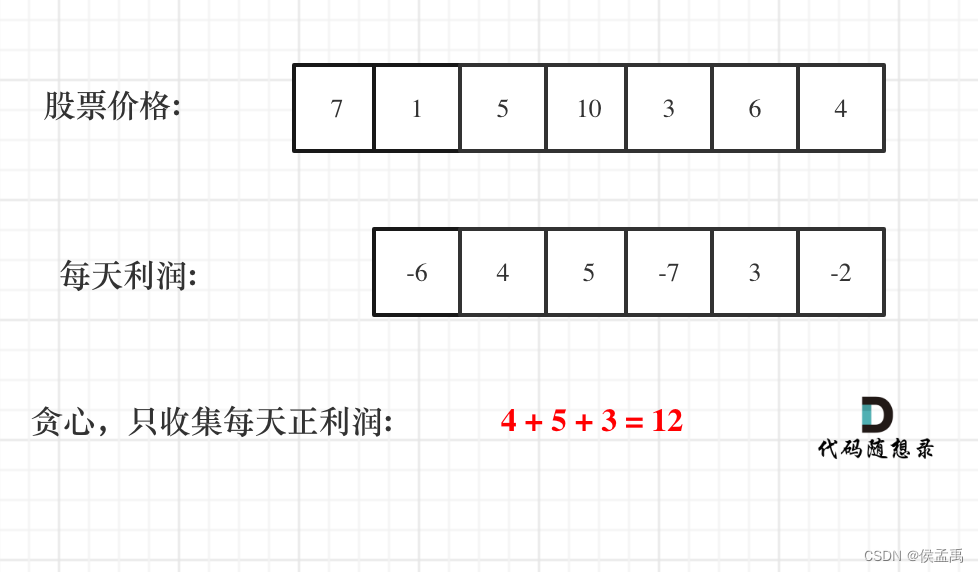
class Solution {
public:
int maxProfit(vector<int>& prices) {
int result = 0;
for (int i = 1; i < prices.size(); i++) {
result += max(prices[i] - prices[i - 1], 0);
}
return result;
}
};55. 跳跃游戏
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
我的想法:
第一版:从后往前推,sum计算从后往前的和,nums[len-2]>1;nums[len-2] + nums[len-3]>2;
代码:
class Solution {
public:
bool canJump(vector<int>& nums) {
if(nums.size() == 1) return true;
if(nums[0] == 0) return false;
int index = nums.size() - 2;
int sum = 0;
int count = 1;
for(int i = index; i >= 0; i--)
{
sum += nums[i];
if(sum < count)
{
return false;
}
count++;
}
return true;
}
};问题:[2,0,0]这样是过不了的
第二版