目录
前言
二叉树的链式存储结构
二叉树的遍历
1.前序遍历
2.中序遍历
3.后序遍历
二叉树的创建
创建一个新节点的函数接口
1.创建二叉树返回根节点
2.已有根节点,创建二叉树
3.已有数据,创建二叉树
前言
在此之前我们学习了二叉树的定义和储存方式,还学了一种特殊的二叉树---堆,那今天我们就正式开始去学习二叉树了,是通过链式结构储存的二叉树,下面我会详细讲解二叉树的创建和遍历方法。
相关链接
二叉树的基础知识点:数据结构-----树和二叉树的定义与性质_Gretel Tade的博客-CSDN博客
堆的相关方法代码实现:数据结构-----堆(完全二叉树)_Gretel Tade的博客-CSDN博客
二叉树的链式存储结构
#include<stdio.h>
#include<stdlib.h>
typedef char ElemType;
typedef struct binarytreenode {
ElemType data; //数据域
struct binarytreenode* left; //左指针
struct binarytreenode* right; //右指针
}BTnode;二叉树的遍历
这里就会有人问了,咦二叉树都没创建呢,就开始学遍历?别急,下面听我慢慢说,二叉树的创建是要利用的遍历的,这么说吧,遍历是贯穿整个二叉树的基础,没有遍历,就不会有二叉树。二叉树的遍历分三种:前序遍历、中序遍历、后序遍历,下面我们接着看。
1.前序遍历
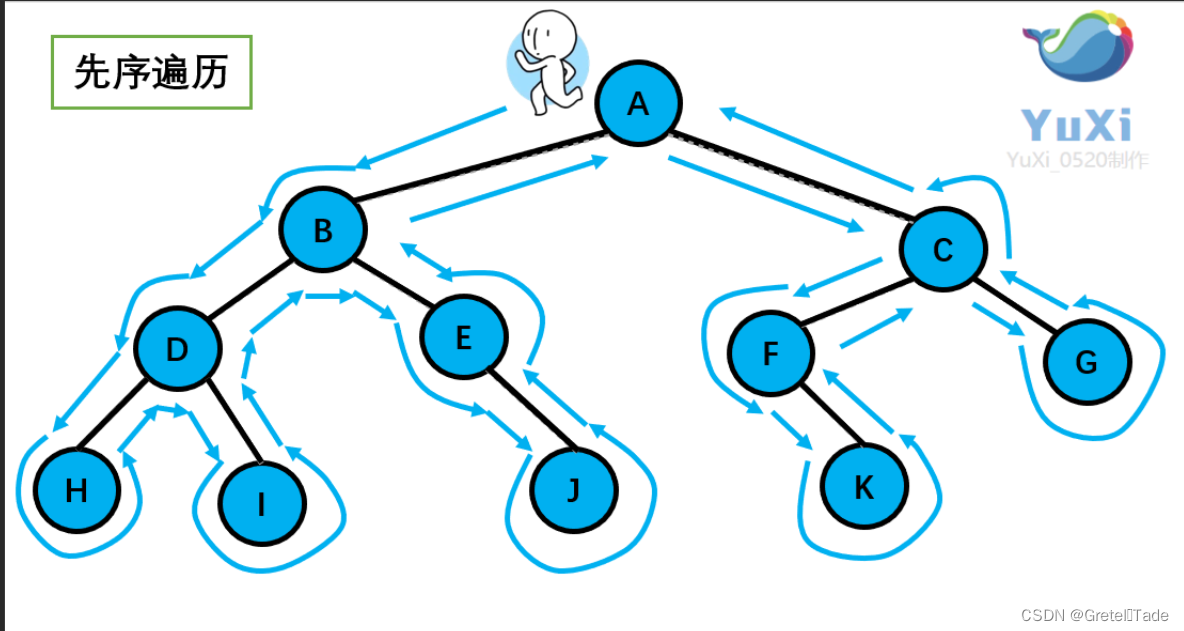
在一个二叉树中,前序遍历就是按照二叉树的外围跑一圈,所以从根节点开始,然后到左节点,跑完全部的左节点,就进入到右节点,最后回到根部节点。如下图所示:
前序遍历的顺序为:根左右
前序遍历结果为: A B D H I E J C F K G
 动图演示:
动图演示:

代码实现
//1.二叉树的前序遍历
void Btree_prev(BTnode* T) { //T 是这个树的根节点
if (!T) {
return;
}
printf("%c ", T->data); //先输出遍历结果
Btree_prev(T->left); //左边节点进入递归
Btree_prev(T->right); //右边节进入递归
}2.中序遍历
中序遍历可以看作是,这个二叉树上的每一个节点垂直落下来,最后排成一排就是遍历完成的结果,如下图所示:
中序遍历的顺序为:左根右
中序遍历结果:H D I B E J A F K C G
 代码实现
代码实现
//2.二叉树的中序遍历
void Btree_mid(BTnode* T) { //T 是这个树的根节点
if (!T) {
return;
}
Btree_prev(T->left);
printf("%c ", T->data);
Btree_prev(T->right);
}3.后序遍历
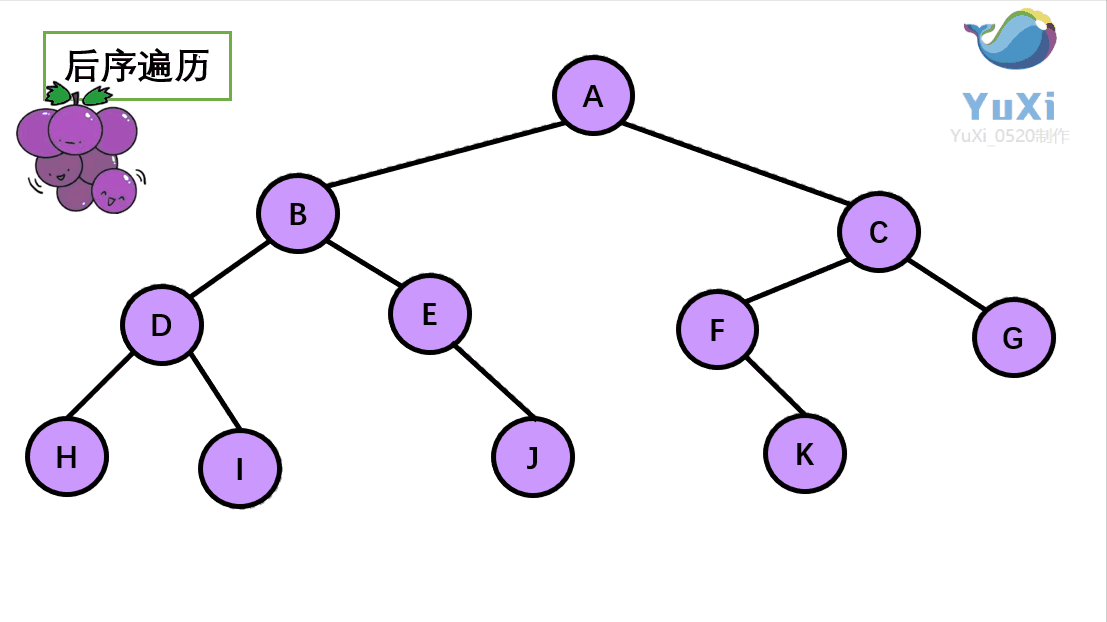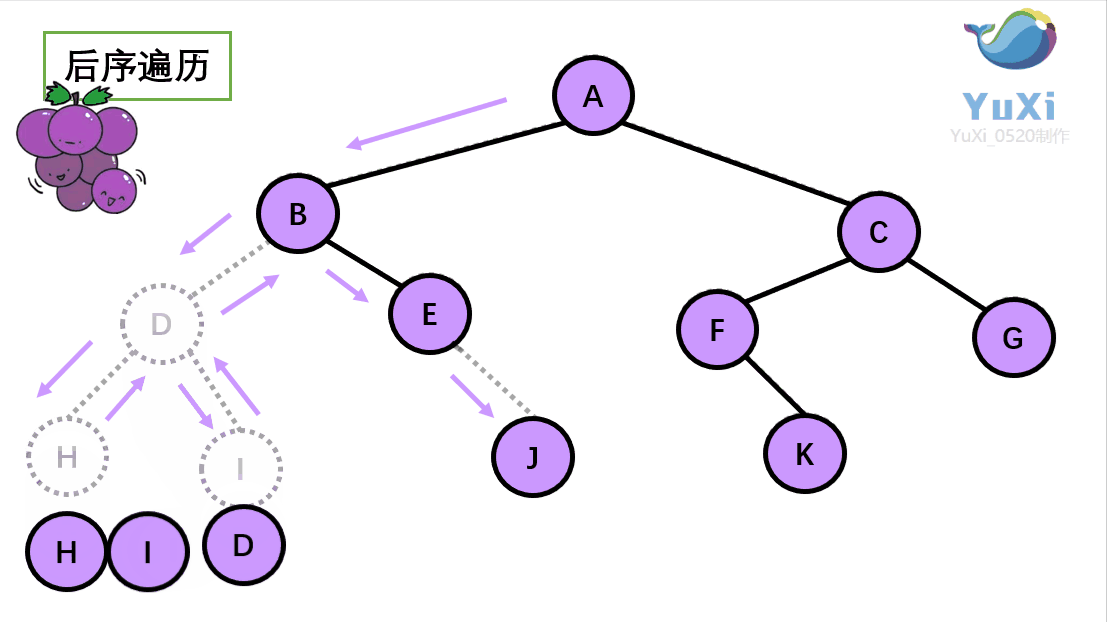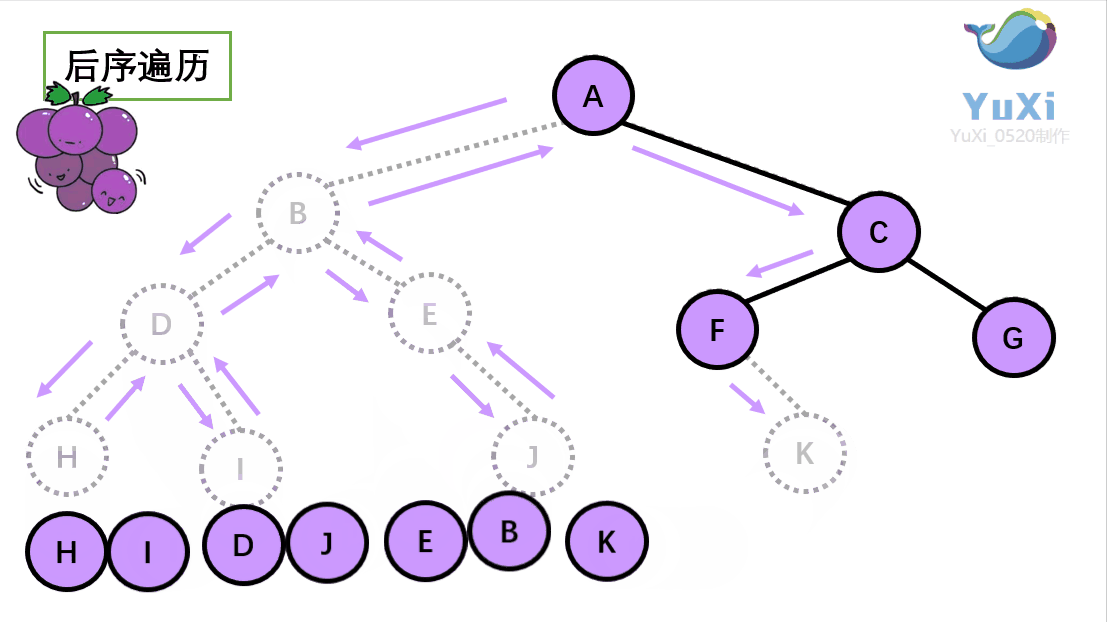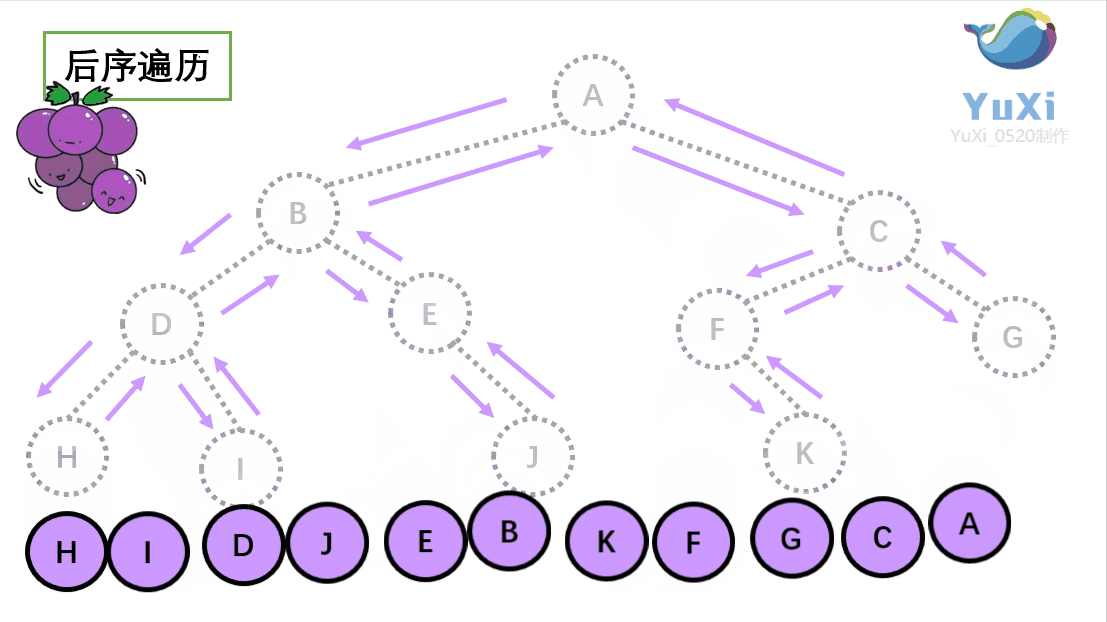
后序遍历可以看作是一个摘葡萄的过程,先是把下面的葡萄摘完,然后再去摘上面的葡萄,也就是把子节点遍历完成了之后,最后去遍历根节点。如下图所示:
后序遍历的顺序为:左右根
后序遍历的结果:H I D J E B K F G C A
代码实现:
//3.后续遍历
void Btree_final(BTnode* T) { //T 是这个树的根节点
if (!T) {
return;
}
Btree_final(T->left);
Btree_final(T->right);
printf("%c ", T->data);
}二叉树的创建
先学会了二叉树的遍历,我们才可以去接着学习怎么来创建一个二叉树。创建二叉树是边遍历边创建的,在创建的过程中遍历,在遍历的过程中创建。二叉树的创建可以通过前面的三种遍历方式去创建,前序遍历、中序遍历、后序遍历都可以去创建一个二叉树,只是长相不太相同,这里我主要去通过前序遍历来创建二叉树,如果你们想通过其他两种方法只需要把代码稍微修改一下就可以实现了,下面我会详细讲解创建二叉树的常见三种写法。
概要说明:
在创建一个二叉树时,我获取到的字符序列是 ABD#E###CF### ,其中#是表示空节点的,字母是表示有数据的节点 那么这个二叉树前序遍历创建后的样子应该如下所示:
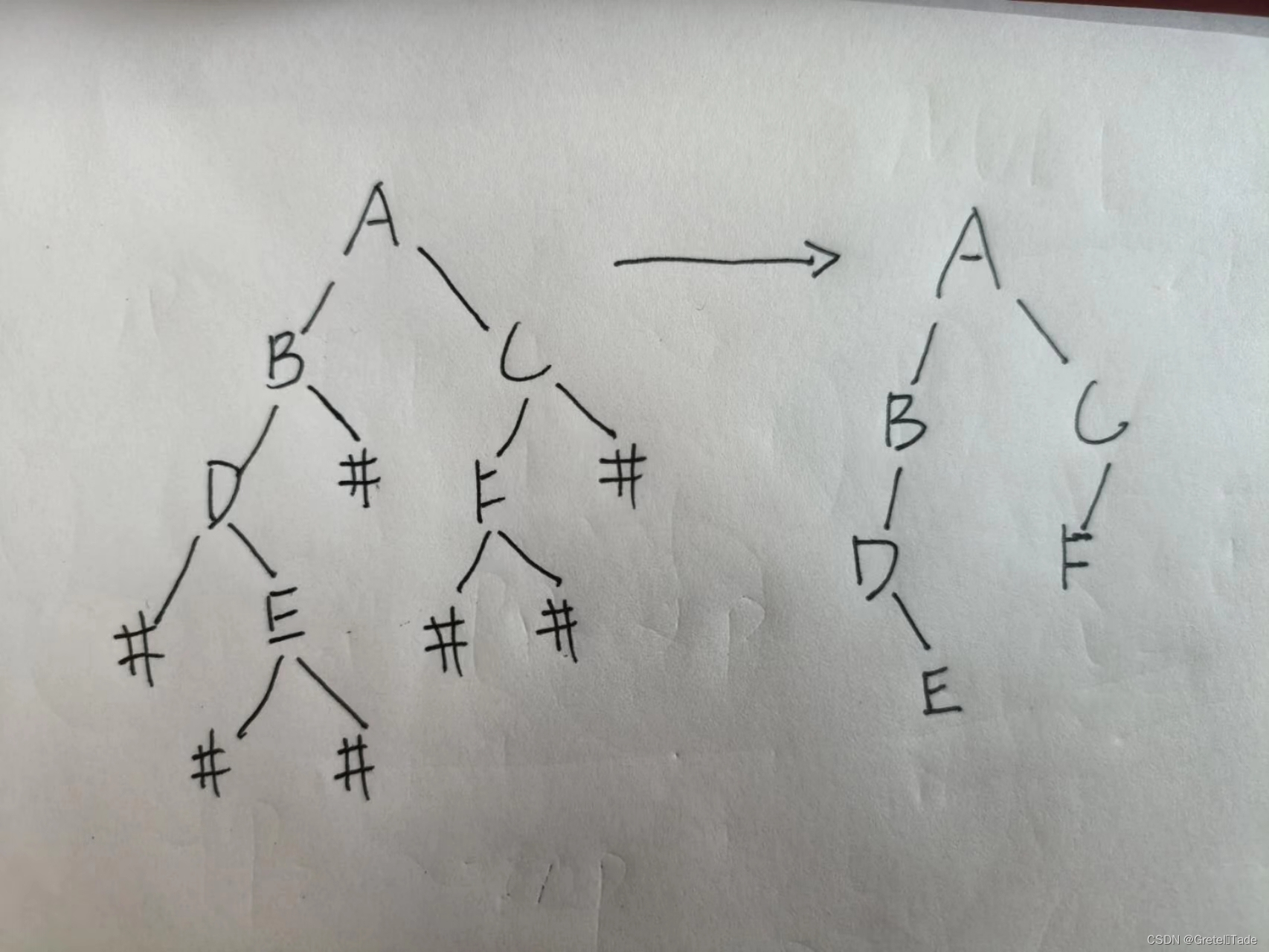
创建一个新节点的函数接口
//创建一个新节点函数接口
BTnode* Create_node(ElemType data) {
BTnode* new_node = (BTnode*)malloc(sizeof(BTnode));
if (!new_node) {
printf("ERROR\n");
exit(-1);
}
//依次赋值初始化
new_node->data = data;
new_node->left = NULL;
new_node->right = NULL;
return new_node;
}下面我就开始介绍创建二叉树的三种常见写法。
1.创建二叉树返回根节点
//创建二叉树返回根节点
BTnode* Create_btree_2() {
char ch;
ch = getchar();
BTnode* root = NULL;
while (ch == ' ')//输入空格无效,重新输入
{
printf("请重新输入\n");
scanf("%c", &ch);
}
if (ch != '#')
{
root = Create_node(ch);
root->left = Create_btree_2(); //左节点递归创建
root->right = Create_btree_2(); //右节点递归创建
}
return root;
}2.已有根节点,创建二叉树
//传入根节点,然后进行创建
void Create_btree_3(BTnode** T) {
char ch;
scanf("%c",&ch);
while(ch==' ') //输入空格无效,重新输入
{
printf("请重新输入\n");
scanf("%c", &ch);
}
if (ch == '#')
(*T) = NULL;
else {
(*T) = Create_node(ch);
Create_btree_3(&(*T)->left);
Create_btree_3(&(*T)->right);
}
}3.已有数据,创建二叉树
对比上面前两种写法不同,这个是已有数据的情况下,通过这个数据来去创建这个二叉树,而上面两种方法是边输入边创建二叉树。
//00_1已有数据,然后创建二叉树,返回根节点
BTnode* Create_btree_1(ElemType *&data){ //&data对变量的引用
BTnode* node=NULL;
if (*data!='#' && data!= NULL) {
node = Create_node(*data);
node->left = Create_btree_1(++data);
node->right = Create_btree_1(++data );
}
return node;
}注意:这里要用到对变量的引用(取别名)来创建,否则会出现错误
好了,以上就是本期的全部内容了,下一期我们接着学习二叉树的相关操作方法,下次见咯!
分享一张壁纸: