💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Simulink仿真、Matlab代码、文献
💥1 概述
文献:

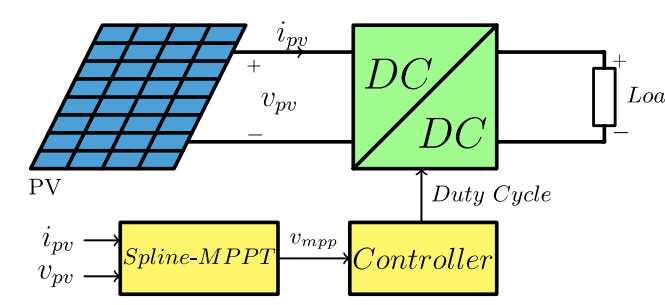
光伏 (PV) 系统中使用的不同最大功率点跟踪 (MPPT) 技术根据简单性、速度和准确性等多个标准进行评估。这些标准之间存在权衡,通常以牺牲速度和简单性为代价来实现更高的精度。本文旨在介绍样条-MPPT技术作为一种快速、准确、简单的方法,用于在光伏组串特性失真的均匀辐照度和部分阴影条件下(PSC)下找到光伏系统的最大功率点。所提出的方法基于三次样条插值,该插值定义了几个采样点的近似函数。文献中提出了几种基于插值的方法,以找到均匀辐照度下的MPP。然而,它们无法在部分阴影条件下找到全局最大功率点(GMPP)。样条-MPPT技术仅使用少量电流和电压样本来估计系统的MPP,并在环境条件保持不变的情况下保持该点。仿真结果证明了所提方法的优越性。
在过去的几十年里,温室气体排放量急剧增加,根据预测,其不断增长的速度将在未来几年继续下去。温室气体的增加导致全球变暖,对地球产生许多深远的影响[1],[2]。燃烧化石燃料发电是造成这一问题的主要原因之一。因此,有必要用适当的替代品代替化石燃料,因为如果不这样做,肯定会产生可怕的后果。光伏能源系统提供无污染、可持续和安全的电力,显示出成为化石燃料的便捷替代品的巨大潜力。由于光伏技术的众多进步,光伏组件的效率大幅提高,而近年来其价格有所下降[3],[4]。尽管光伏系统在某些地区是价格最低的选择,但在其他一些地区,风电场和天然气发电厂比光伏系统更实惠[1],[5]。然后,尚未进行进一步的研究以提高光伏系统的渗透率。太阳能系统的经济性与从光伏组件中提取的功率量密切相关。此外,在光伏系统中,由于P-V曲线的非线性行为,只有一个最佳工作点,即最大功率点(MPP)。MPP在P-V曲线上的位置在很大程度上取决于环境条件,例如辐照度和温度。此外,在部分阴影条件(PSC)下,由于云,树木和建筑物的阴影,串联串中的不同模块受到不相等的辐照度,P-V曲线变得失真。在这种情况下,P-V曲线上会出现几个局部最大功率点(LMPP)和一个全局最大功率点(GMPP),导致收集最大可用能量的过程变得复杂。
传统的MPPT方法,如扰动和观察(P&O),爬山(HC)和增量电导(INC)在部分阴影条件下无法找到GMPP,因为它们可能被困在局部最大功率点之一中。跟踪速度慢是这些方法在PSC下的另一个缺点。但是,这些方法与其他方法一起使用以查找GMPP。例如,0.8V超频[6]中提出的方法使用开路电压(OCV)方法的概念,通过假设峰值位于0.8开路电压V处来找到峰值(LMPP和GMPP)的近似位置超频.到达一个峰的估计位置后,该方法切换到P&O方法以达到峰的最大点。对其他峰重复此过程,直到找到GMPP。[7] 中的作者使用类似的方法并结合 0.8V超频方法与公司。这两项研究假设,在从一个峰值到另一个峰值向GMPP移动的过程中,峰值的幅度增加。换句话说,峰值越接近GMPP,它的幅度就越高。因此,当它们到达一个较低星等的峰时,它们会停止扫描该方向的其他峰。然而,在实践中,峰值并不总是按GMPP的升序排列[8],因此在某些情况下,这些方法可能会忽略GMPP。此外,使用两种不同的方法会导致跟踪过程缓慢。[9]中提出的方法在第一步中使用全局MPPT程序,通过该过程将几个电压样本施加到PV模块上。然后,检测具有最高功率的样品,并使用P&O细化GMPP的位置。整个过程每15分钟重复一次,以找到可能由大气变化引起的新GMPP。这是减轻大气变化影响的唯一策略,该方法无法立即响应变化。
基于人工神经网络(ANN)和模糊逻辑控制(FLC)的软计算技术在部分着色条件下表现不佳[10]。然而,已经提出了ANN和FLC与各种其他方法的组合来提高其性能[11]。显然,将ANN和FLC与其他方法一起使用会增加跟踪过程的复杂性。进化优化方法,如粒子群优化(PSO)[12],人工蜂群(ABC)[13],灰狼优化(GWO)[14],差分进化(DE)[15]和蚁群优化(ACO)[16]是用于查找GMPP的其他流行方法。 需要相对较高的迭代次数来收敛、对初始设计的依赖性和实现复杂性是这些方法的普遍缺点。
科学中使用了各种数据拟合和近似方法来定义各种现象的函数[17],[18]。对于一组给定的采样点,近似方法定义了一个函数,该函数正确表示采样点的行为。曲线拟合和插值是两种最常见的近似方法,在一些论文中使用,以找到光伏系统的最大功率点。[19]–[21]的作者使用不同的曲线拟合方法来查找MPP。[19]中提出的方法使用曲线拟合法和六阶多项式来估计多晶硅电池的P-V曲线。虽然它能准确地找到MPP,但它使用递归最小二乘法和牛顿-拉夫森方法,这些方法相当复杂和耗时。[20]中引入的基于曲线拟合的方法使用大量的采样点和复杂的过程,这使得它不太适合MPPT应用。在[21]中,该算法使用6个点通过有点复杂的过程来估计I-V曲线,而其提取的功率始终小于简单的P&O方法。[22]中提出的分析方法通过估计I-V曲线来找到MPP。不幸的是,与传统方法相比,这种方法产生的能量更少。在持续的环境变化过程中缺乏跟踪策略是该方法的另一个弱点。此外,[19]–[22]中提出的所有方法都无法在部分阴影条件下找到全局最大功率点。[23] 和 [24] 中提出的方法是 [25] 和 [26] 的主要参考,使用二次插值法估计 MPP。由于二次插值不够精确,无法近似P-V曲线,因此该方法必须使用多次迭代和占空比过程才能获得适当的结果。此外,该方法仅在均匀辐照度下有效,不能解决部分阴影条件下的最大功率点跟踪问题。[27]中提出的方法采用曲线拟合法在局部阴影条件下检测GMPP。除了耗时的过程外,它还仅限于两个辐照度水平。但是,在现实世界中,阴影模式比假设的模式复杂得多。[28]中的分析方法也旨在发现部分阴影条件下的GMPP。该方法通过从曲线中抽取少量样本,将I-V曲线划分为几个较小的子区域。然后,它估计每个次区域的曲线,以保留当之无愧的次区域并丢弃其他次区域。该方法重复此过程,直到达到GMPP。不幸的是,作者没有提供有关其方法效率的任何信息。在[29]中,作者使用组合方法来查找光伏组件的MPPT。第一步,该方法使用三阶多项式插值法确定MPP在I-V曲线上的大致位置,然后使用PSO找到最大功率点的确切位置。然而,作者没有解释他们选择样本点的策略。不准确的插值,加上不正确的采样点,导致完全错误的初级估计。此外,使用两种不同的方法增加了MPPT技术的复杂性。
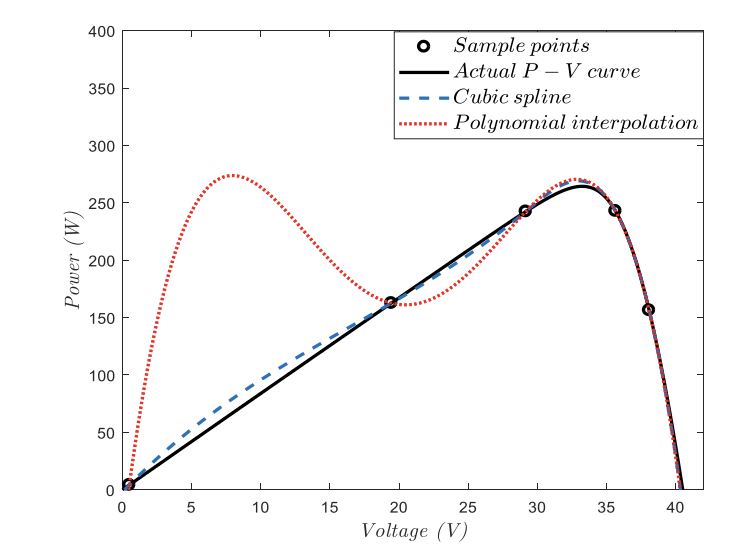
在多项式插值中,估计函数通过所有采样点;因此,该方法得到的P-V曲线仅在采样点附近准确。另一方面,为了向电网提供辅助服务,应准确估计光伏组件的整体P-V特性。增加采样点可以导致多项式的次数更高,从而可以在P-V曲线的整个域上产生更精确的近似。另一方面,它也可能是估计函数中不希望的高振幅振荡的来源。
本文旨在利用样条-MPPT方法求出均匀辐照度和局部阴影条件下的最大功率点。基于三次样条插值的样条-MPPT作为一种高效的MPPT方法具有一些优点,使其更适合于最大功率点跟踪。这种插值方法通过一个简单的过程定义了分段三度平滑函数。样条-MPPT使用少量采样点来查找最大功率的电压,并保持在该电压下而不会在其周围波动。第二部分将回顾三次样条插值的基本概念。第三和第四部分描述了均匀辐照度和局部阴影条件下的样条-MPPT方法。该方法在第五部分中进行了验证。最后,给出了结论。
📚2 运行结果

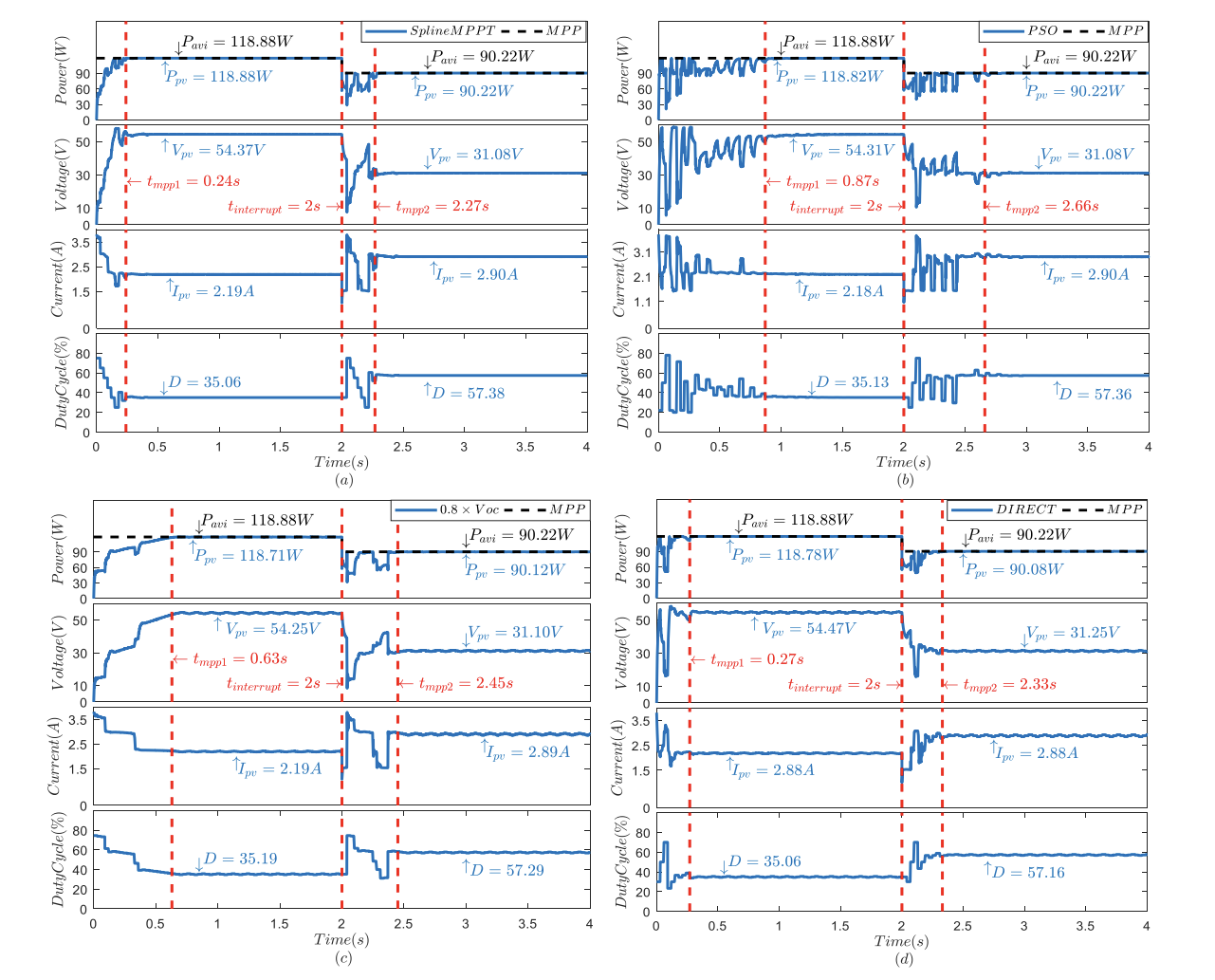
版本Matlab2020a
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。