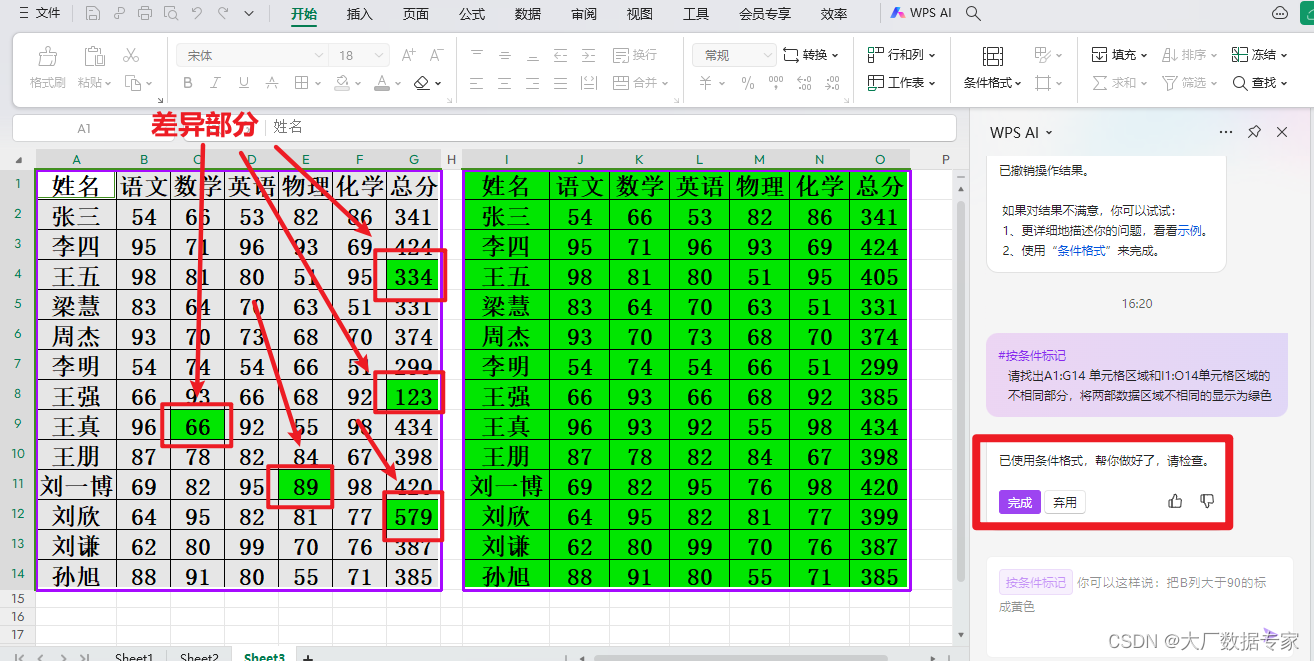
一般像素坐标系转相机坐标系都是默认相机是水平的,没有考虑相机有俯仰角的情况,大致的过程是:像素坐标系统-->图像坐标系-->相机坐标系 ->世界坐标系或雷达坐标系:
像素坐标系
像素坐标系(u,v)是以pixel为单位的离散图像坐标,原点在图片的左上角
图像坐标系
图像坐标系(x,y)是以米或毫米为单位(真实的物理尺寸)的连续图像坐标,以图片对角线交点作为基准原点
相机坐标系
相机坐标系(Xc,Yc,Zc)原点在相机的光心上,Z轴与相机光轴平行,即相机的镜头拍摄方向
世界坐标系
世界坐标系(Xw,Yw,Zw)是标示目标物体空间位置的参考系,可根据需要自由设置原点位置
雷达坐标系
雷达坐标系通常是以前进方向为x轴正向,左侧为y轴正向,向上为z轴正向
像素坐标系和图像坐标系的关系
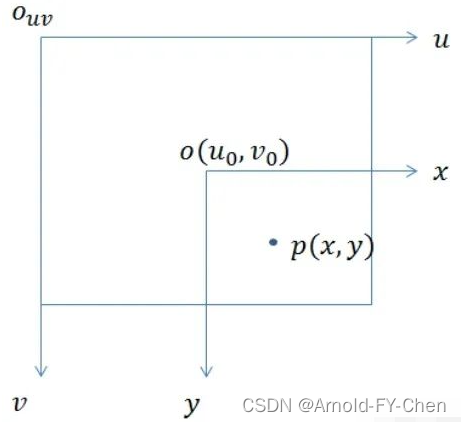

其中,dx指一个像素代表的物理尺寸上的宽度,与x同单位,x/dx表示像素点在x轴方向偏离图像坐标系中心多少个像素,同样y/dy表示像素点在y轴方向偏离图像坐标系中心多少个像素,(u0,v0)是图像平面中心,是图像坐标系的原点。
图像坐标系和相机坐标系的关系
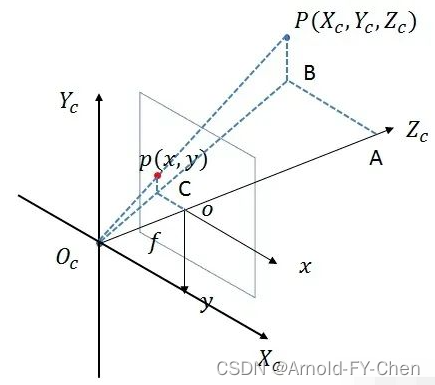
根据相似三角形边长等比原理可推导出相机坐标系下的空间物理点P(Xc,Yc,Zc)在图像坐标系下的投影点p(x,y)之间的关系:
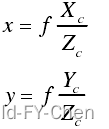
世界坐标系或雷达坐标系和相机坐标系的关系
世界坐标系或雷达坐标系和相机坐标系之都是空间3D坐标系,因此他们之间只需要通过旋转和平移来转换,例如相机坐标系和世界坐标系之间的转换可以表示成:
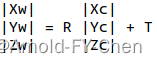
其中旋转可能分别需要拆解为分别绕x、y、z轴旋转来完成(也可能只需要其中一部分就完成了旋转,根据实际需要定):
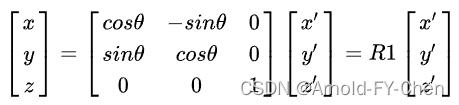
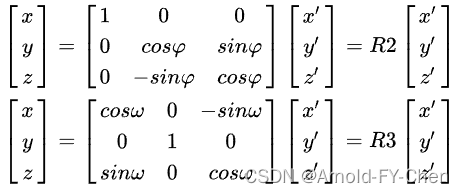
假如分别绕x、y、z轴旋转都需要,则最终的旋转矩阵R = R1*R2*R3,维度为3x3。T为平移矩阵,维度为3x1。用齐次坐标表示相机坐标系和世界坐标系之间的关系为:
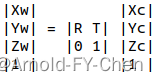
上述转换方法对相机坐标系转雷达坐标系同样适用。
如果是将世界坐标系转相机坐标系,上面的旋转矩阵为逆矩阵,平移矩阵里各元素取相反值而已。
当相机有俯仰角时,像素坐标系转世界坐标系或雷达坐标系,关键在于测出相机俯仰角然后将坐标乘以旋转矩阵转换到相机为水平时的坐标系下去,可参见这篇博文:相机安装位置之相对于地面的俯仰角的标定_相机俯仰角_AndyCheng_hgcc的博客-CSDN博客
如果对精度要求不高,且有相机坐标系或雷达坐标系下的可视化效果看转换后的效果,可以直接调节图像坐标系下的坐标值,因为当相机有俯仰角时,物体在图像上的成像像素点和相机水平时的对应成像像素点比发生了向上或向下的偏移,在转换为图像坐标系之前试着对物体的每个成像像素点减去或加上这些偏移量,可以看到,图像上的物体点投到到雷达坐标系下后能比较准确地和物体在3D空间中的位置贴合。