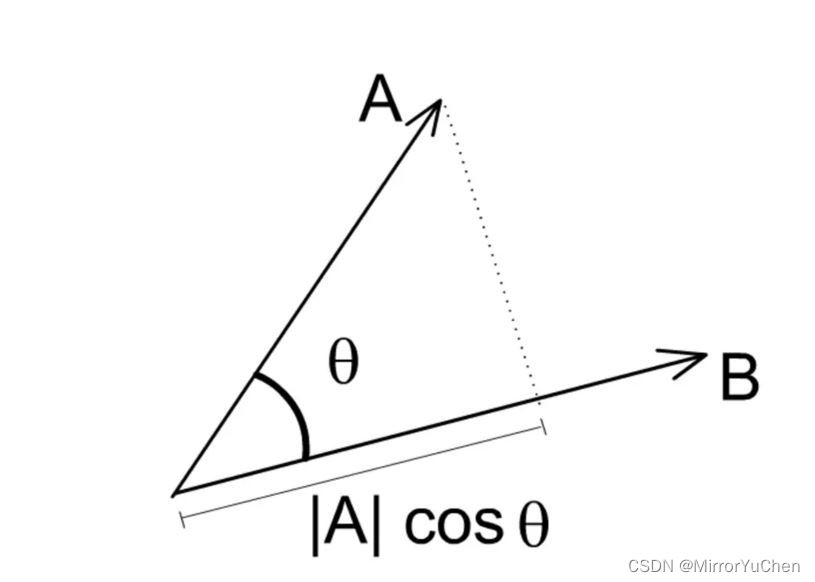
1.点乘
A ⃗ ⋅ B ⃗ = ∣ A ⃗ ∣ ∣ B ⃗ ∣ c o s ⟨ A ⃗ , B ⃗ ⟩ \vec{A} \cdot \vec{B} = \left | \vec{A} \right | \left | \vec{B} \right | cos\left \langle \vec{A}, \vec{B} \right \rangle A⋅B= A B cos⟨A,B⟩
- 对应几何意义:向量
A
⃗
\vec{A}
A在向量
B
⃗
\vec{B}
B方向上投影与
∣
B
⃗
∣
\left | \vec{B} \right |
B
的乘积,反应两个向量在方向上的相似度,结果越大越相似;
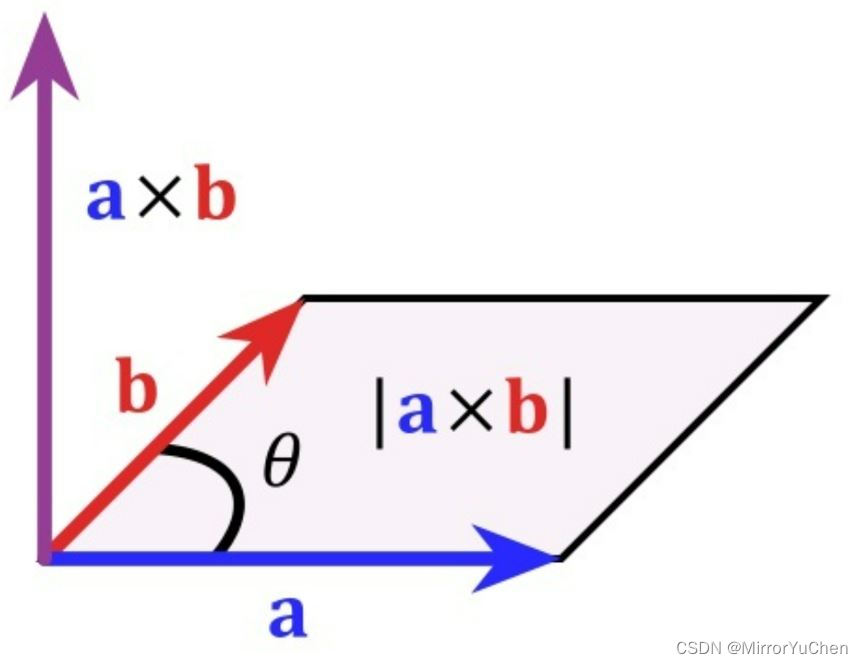
2.叉乘
A ⃗ × B ⃗ = ∣ A ⃗ ∣ ∣ B ⃗ ∣ s i n ⟨ A ⃗ , B ⃗ ⟩ n ⃗ \vec{A} \times \vec{B} = \left | \vec{A} \right | \left | \vec{B} \right | sin\left \langle \vec{A}, \vec{B} \right \rangle \vec{n} A×B= A B sin⟨A,B⟩n
- 其中 n ⃗ \vec{n} n为 A ⃗ \vec{A} A与 B ⃗ \vec{B} B所构成平面的单位向量。
- 对应几何意义:若以
A
⃗
\vec{A}
A和
B
⃗
\vec{B}
B为边构成一个平行四边形,那么这两个向量外积的模长与这个平行四边形的面积相等;
3.罗德里格斯公式的特殊情形
-
如图所示,假设向量 k ⃗ \vec{k} k为与Z轴重合的单位向量,向量 v ⃗ \vec{v} v与X轴重合,向量 v ⃗ \vec{v} v绕向量 k ⃗ \vec{k} k旋转 θ \theta θ角度后,得到向量 v ⃗ r o t \vec{v}_{rot} vrot:
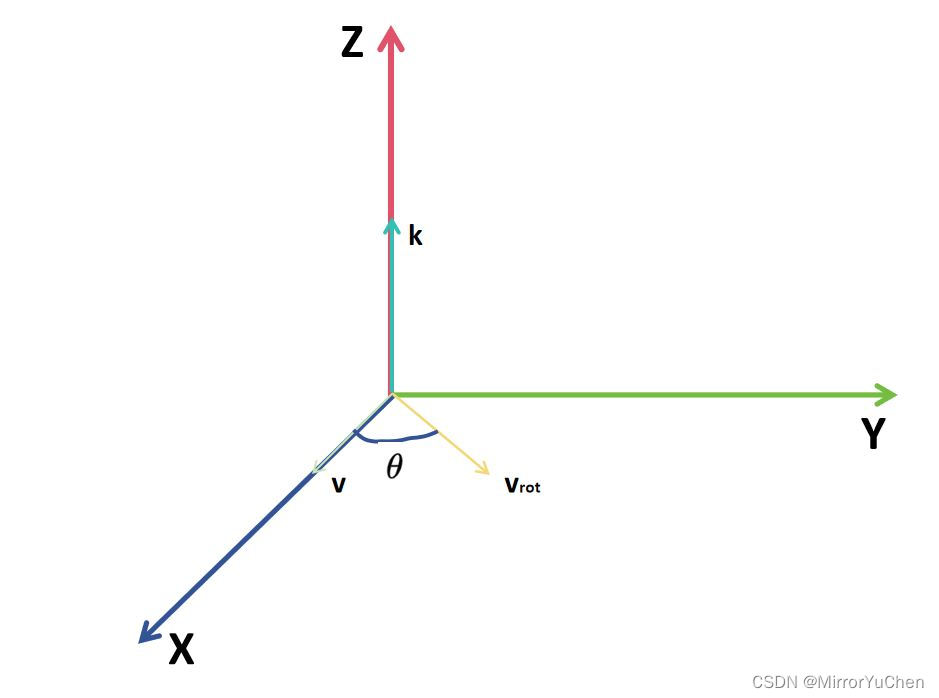
-
那么,Y轴方向的单位向量为:
Y ⃗ = k ⃗ × v ⃗ ∣ k ⃗ × v ⃗ ∣ \vec{Y} = \frac{\vec{k}\times \vec{v}}{|\vec{k}\times \vec{v}|} Y=∣k×v∣k×v -
而向量 k ⃗ \vec{k} k和向量 v ⃗ \vec{v} v垂直,并且向量 k ⃗ \vec{k} k为单位向量,则:
Y ⃗ = k ⃗ × v ⃗ ∣ k ⃗ × v ⃗ ∣ = k ⃗ × v ⃗ ∣ k ⃗ ∣ ∣ v ⃗ ∣ s i n ⟨ k ⃗ , v ⃗ ⟩ = k ⃗ × v ⃗ ∣ v ⃗ ∣ \vec{Y} = \frac{\vec{k}\times \vec{v}}{|\vec{k}\times \vec{v}|} = \frac{\vec{k}\times \vec{v}}{|\vec{k}| | \vec{v}| sin\left \langle \vec{k}, \vec{v} \right \rangle} = \frac{\vec{k}\times \vec{v}}{|\vec{v}|} Y=∣k×v∣k×v=∣k∣∣v∣sin⟨k,v⟩k×v=∣v∣k×v -
那么旋转后的向量 v r o t v_{rot} vrot为:
v ⃗ r o t = ∣ v ⃗ r o t ∣ c o s θ v ⃗ ∣ v ⃗ ∣ + ∣ v ⃗ r o t ∣ s i n θ Y ⃗ ∣ Y ⃗ ∣ \vec{v}_{rot} = |\vec{v}_{rot}|cos\theta \frac{\vec{v}}{|\vec{v}|} + |\vec{v}_{rot}|sin\theta \frac{\vec{Y}}{|\vec{Y}|} vrot=∣vrot∣cosθ∣v∣v+∣vrot∣sinθ∣Y∣Y -
由于旋转不会改变向量模长,所以 ∣ v ⃗ ∣ = ∣ v ⃗ r o t ∣ |\vec{v}| = |\vec{v}_{rot}| ∣v∣=∣vrot∣,向量 Y ⃗ \vec{Y} Y为归一化后的单位向量,所以:
v ⃗ r o t = c o s θ v ⃗ + s i n θ ( k ⃗ × v ⃗ ) \vec{v}_{rot} = cos\theta \vec{v} + sin\theta (\vec{k} \times \vec{v}) vrot=cosθv+sinθ(k×v)
4.罗德里格斯公式的一般形式
-
如图所示,向量 v ⃗ \vec{v} v绕向量 k ⃗ \vec{k} k旋转 θ \theta θ角度得到向量 v ⃗ r o t \vec{v}_{rot} vrot,其中,向量 k ⃗ \vec{k} k为单位向量:
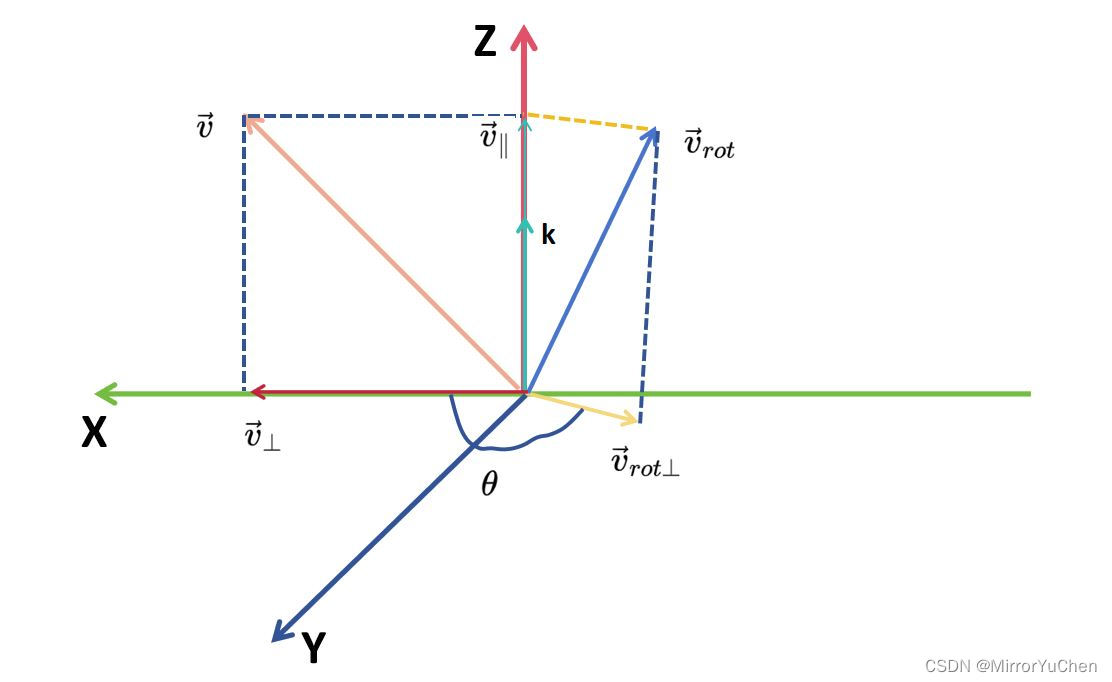
-
向量 v ⃗ \vec{v} v可以表示成如下形式:
v ⃗ = v ⃗ ∥ + v ⃗ ⊥ v ⃗ r o t = v ⃗ ∥ + v ⃗ r o t ⊥ \vec{v} = \vec{v}_{\parallel } + \vec{v}_{\perp } \\ \vec{v}_{rot} = \vec{v}_{\parallel} + \vec{v}_{rot\perp } v=v∥+v⊥vrot=v∥+vrot⊥ -
由于向量 k ⃗ \vec{k} k为单位向量,有:
v ⃗ ∥ = ∣ v ⃗ ∣ c o s ⟨ v ⃗ , k ⃗ ⟩ k ⃗ ∣ k ⃗ ∣ = ∣ v ⃗ ∣ v ⃗ ⋅ k ⃗ ∣ v ⃗ ∣ ∣ k ⃗ ∣ k ⃗ ∣ k ⃗ ∣ = v ⃗ ⋅ k ⃗ ⋅ k ⃗ \vec{v}_{\parallel } = |\vec{v}|cos\left \langle \vec{v}, \vec{k} \right \rangle \frac{\vec{k}}{|\vec{k}|} = |\vec{v}| \frac{\vec{v} \cdot \vec{k}}{|\vec{v}||\vec{k}|}\frac{\vec{k}}{|\vec{k}|} = \vec{v} \cdot \vec{k} \cdot \vec{k} v∥=∣v∣cos⟨v,k⟩∣k∣k=∣v∣∣v∣∣k∣v⋅k∣k∣k=v⋅k⋅k -
那么向量 v ⃗ \vec{v} v在垂直方向分量为:
v ⃗ ⊥ = v ⃗ − v ⃗ ∥ = v ⃗ − v ⃗ ⋅ k ⃗ ⋅ k ⃗ \vec{v}_{\perp } = \vec{v} - \vec{v}_{\parallel } = \vec{v} - \vec{v} \cdot \vec{k} \cdot \vec{k} v⊥=v−v∥=v−v⋅k⋅k -
将 v ⃗ ⊥ \vec{v}_{\perp } v⊥绕向量 k ⃗ \vec{k} k旋转 θ \theta θ角度到向量 v ⃗ r o t ⊥ \vec{v}_{rot\perp } vrot⊥等价于上面罗德里格斯公式的特殊情形,直接代入公式有:
v ⃗ r o t ⊥ = c o s θ v ⃗ ⊥ + s i n θ ( k ⃗ × v ⃗ ⊥ ) = c o s θ ( v ⃗ − v ⃗ ⋅ k ⃗ ⋅ k ⃗ ) + s i n θ ( k ⃗ × v ⃗ ⊥ ) \vec{v}_{rot\perp } = cos\theta \vec{v}_{\perp } + sin\theta (\vec{k} \times \vec{v}_{\perp }) = cos\theta (\vec{v} - \vec{v} \cdot \vec{k} \cdot \vec{k}) + sin\theta (\vec{k} \times \vec{v}_{\perp }) vrot⊥=cosθv⊥+sinθ(k×v⊥)=cosθ(v−v⋅k⋅k)+sinθ(k×v⊥) -
所以,旋转后向量 v ⃗ r o t \vec{v}_{rot} vrot为:
v ⃗ r o t = v ⃗ ⋅ k ⃗ ⋅ k ⃗ + c o s θ ( v ⃗ − v ⃗ ⋅ k ⃗ ⋅ k ⃗ ) + s i n θ ( k ⃗ × v ⃗ ⊥ ) = c o s θ v ⃗ + ( 1 − c o s θ ) v ⃗ ⋅ k ⃗ ⋅ k ⃗ + s i n θ ( k ⃗ × v ⃗ ⊥ ) \vec{v}_{rot} = \vec{v} \cdot \vec{k} \cdot \vec{k} + cos\theta (\vec{v} - \vec{v} \cdot \vec{k} \cdot \vec{k}) + sin\theta (\vec{k} \times \vec{v}_{\perp }) \\ = cos\theta \vec{v} + (1 - cos\theta)\vec{v} \cdot \vec{k} \cdot \vec{k} + sin\theta(\vec{k} \times \vec{v}_{\perp }) vrot=v⋅k⋅k+cosθ(v−v⋅k⋅k)+sinθ(k×v⊥)=cosθv+(1−cosθ)v⋅k⋅k+sinθ(k×v⊥) -
由叉乘的几何意义可知, k ⃗ × v ⃗ ⊥ \vec{k} \times \vec{v}_{\perp } k×v⊥和 k ⃗ × v ⃗ \vec{k} \times \vec{v} k×v方向相同,都是向量 v ⃗ , k ⃗ \vec{v},\vec{k} v,k平面法向量方向,也即是图中Y轴方向,二者大小为:
k ⃗ × v ⃗ ⊥ = ∣ k ⃗ ∣ ∗ ∣ v ⃗ ⊥ ∣ n ⃗ k ⃗ × v ⃗ = ∣ k ⃗ ∣ ∗ ( ∣ v ⃗ ∣ s i n ⟨ k ⃗ , v ⃗ ⟩ ) n ⃗ = ∣ k ⃗ ∣ ∗ ∣ v ⃗ ⊥ ∣ n ⃗ = k ⃗ × v ⃗ ⊥ \vec{k} \times \vec{v}_{\perp } = |\vec{k}|*|\vec{v}_{\perp }| \vec{n}\\ \vec{k} \times \vec{v} = |\vec{k}|*(|\vec{v}|sin\left \langle \vec{k}, \vec{v} \right \rangle) \vec{n} \\ = |\vec{k}|*|\vec{v}_{\perp }| \vec{n} \\ = \vec{k} \times \vec{v}_{\perp } k×v⊥=∣k∣∗∣v⊥∣nk×v=∣k∣∗(∣v∣sin⟨k,v⟩)n=∣k∣∗∣v⊥∣n=k×v⊥ -
因此,得到罗德里格斯公式的一般形式:
v ⃗ r o t = c o s θ v ⃗ + ( 1 − c o s θ ) v ⃗ ⋅ k ⃗ ⋅ k ⃗ + s i n θ ( k ⃗ × v ⃗ ) \vec{v}_{rot} = cos\theta \vec{v} + (1 - cos\theta)\vec{v} \cdot \vec{k} \cdot \vec{k} + sin\theta(\vec{k} \times \vec{v}) vrot=cosθv+(1−cosθ)v⋅k⋅k+sinθ(k×v)
5.罗德里格斯公式的矩阵形式
- 将旋转表示成一个矩阵
R
R
R的形式,即:
v ⃗ r o t = R . v ⃗ \vec{v}_{rot} = R.\vec{v} vrot=R.v
-(1) v ⃗ ⋅ k ⃗ ⋅ k ⃗ \vec{v} \cdot \vec{k} \cdot \vec{k} v⋅k⋅k
v ⃗ ⋅ k ⃗ ⋅ k ⃗ = ( v ⃗ ⋅ k ⃗ ) ⋅ k ⃗ = k ⃗ ( v ⃗ ⋅ k ⃗ ) = k ⃗ ( k ⃗ T ⋅ v ⃗ ) = k ⃗ ( k ⃗ T ⋅ v ⃗ ) = ( k ⃗ k ⃗ T ) v ⃗ \vec{v} \cdot \vec{k} \cdot \vec{k} \\ = (\vec{v} \cdot \vec{k}) \cdot \vec{k} \\ = \vec{k}(\vec{v} \cdot \vec{k}) \\ = \vec{k}(\vec{k}^{T}\cdot \vec{v}) \\ = \vec{k}(\vec{k}^{T}\cdot \vec{v}) \\ = (\vec{k} \vec{k}^{T}) \vec{v} v⋅k⋅k=(v⋅k)⋅k=k(v⋅k)=k(kT⋅v)=k(kT⋅v)=(kkT)v - (2)
k
⃗
×
v
⃗
\vec{k} \times \vec{v}
k×v
k ⃗ × v ⃗ = k ⃗ ∧ v ⃗ \vec{k} \times \vec{v} = \vec{k}\wedge \vec{v} k×v=k∧v - 代入得到:
R = c o s θ I + ( 1 − c o s θ ) k ⃗ k ⃗ T + s i n θ k ⃗ ∧ R = cos\theta I + (1-cos\theta)\vec{k}\vec{k}^{T} + sin\theta\vec{k}\wedge R=cosθI+(1−cosθ)kkT+sinθk∧ - 由于
t
r
(
I
)
=
3
,
t
r
(
k
⃗
k
⃗
T
)
=
∣
∣
k
⃗
∣
∣
=
1
,
t
r
(
k
⃗
∧
)
=
0
tr(I) = 3,tr(\vec{k}\vec{k}^{T})=||\vec{k}|| = 1,tr({\vec{k}\wedge})=0
tr(I)=3,tr(kkT)=∣∣k∣∣=1,tr(k∧)=0,那么:
t r ( R ) = 3 c o s θ + ( 1 − c o s θ ) = 2 c o s θ + 1 θ = a r c c o s ( t r ( R ) − 1 2 ) tr(R)=3cos\theta +(1-cos\theta) = 2cos\theta + 1 \\ \theta = arccos(\frac{tr(R)-1}{2}) tr(R)=3cosθ+(1−cosθ)=2cosθ+1θ=arccos(2tr(R)−1)
6.参考资料
- [1] 罗德里格斯公式推导
- [2] 向量点乘和叉乘的意义