给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

示例 1：

输入：root = [1,null,3,2,4,null,5,6]
输出：3

示例 2：

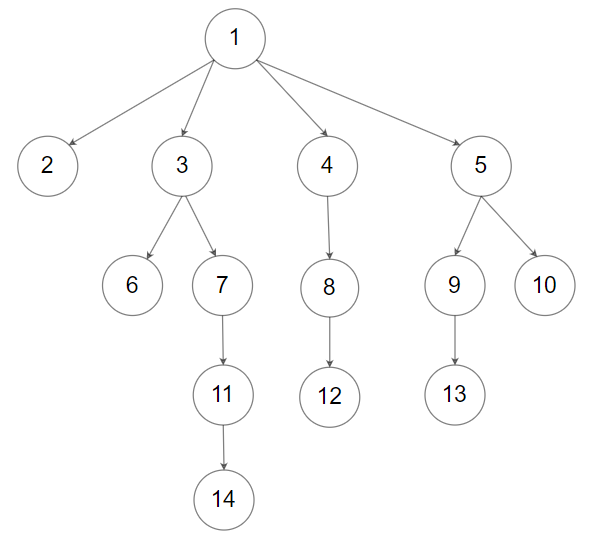
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：5

class Solution {
public:
    int maxDepth(Node* root) {
        //层序遍历
        queue<Node*>que;
        int count = 0;
        if(!root) return count;
        que.push(root);
        while(!que.empty()){
            int num =  que.size();
            count++;
            while(num--){
                Node* node = que.front();
                que.pop();
                for(int i = 0;i < node->children.size();i++){
                    if(node->children[i])que.push(node->children[i]);
                } 
            }
        }
        return count;
    }
};

//dfs
class Solution {
public:
    int dfs(Node* root){
        if(!root) return 0;
        int res = 0;
        for(int i = 0;i < root->children.size();i++){
            res = max(res,dfs(root->children[i]));
        }
        return res+1;
    }
    int maxDepth(Node* root) {
        //dfs
        return dfs(root);
    }
};