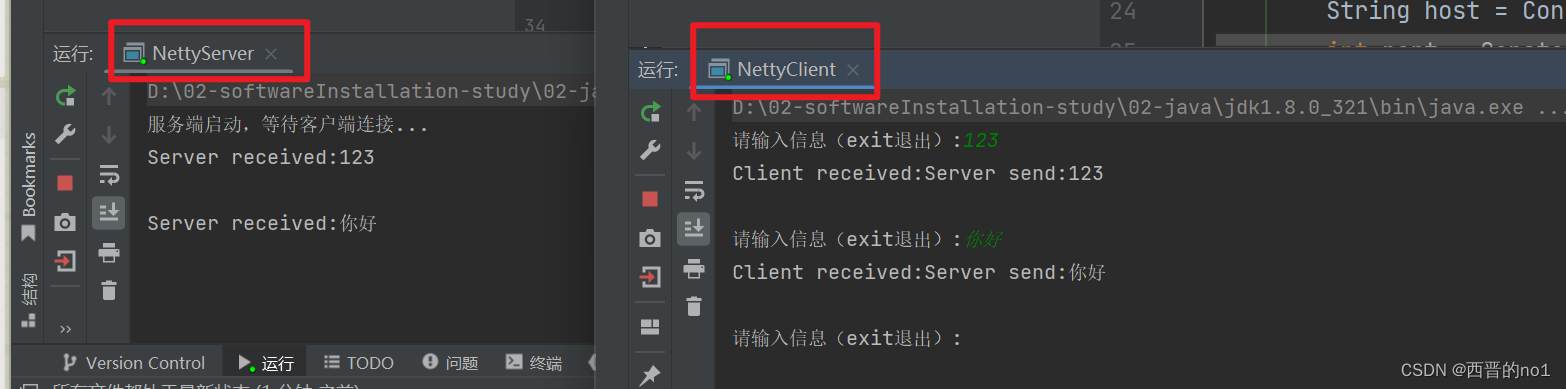
Jmeter多用户并发测试

第1步， 在安装目录下的bin文件夹下打开Jmeter，如下图

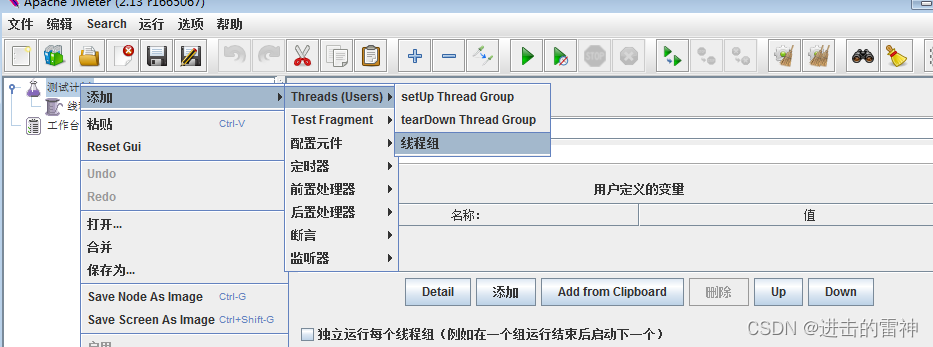
第2步，新建一个线程组

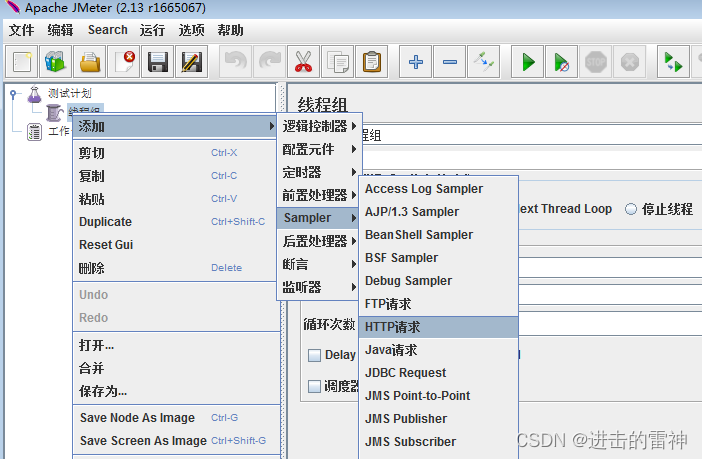
第3步，新建一个HTTP请求，这里给这个请求重命名为getMsgSum

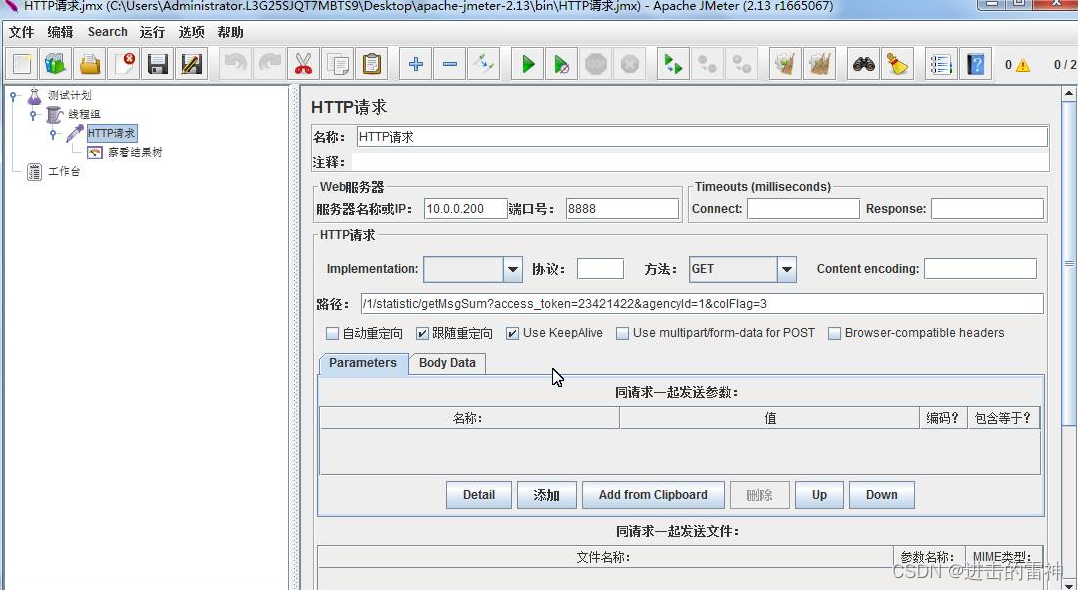
设置HTTP请求的IP端口，以及路径等

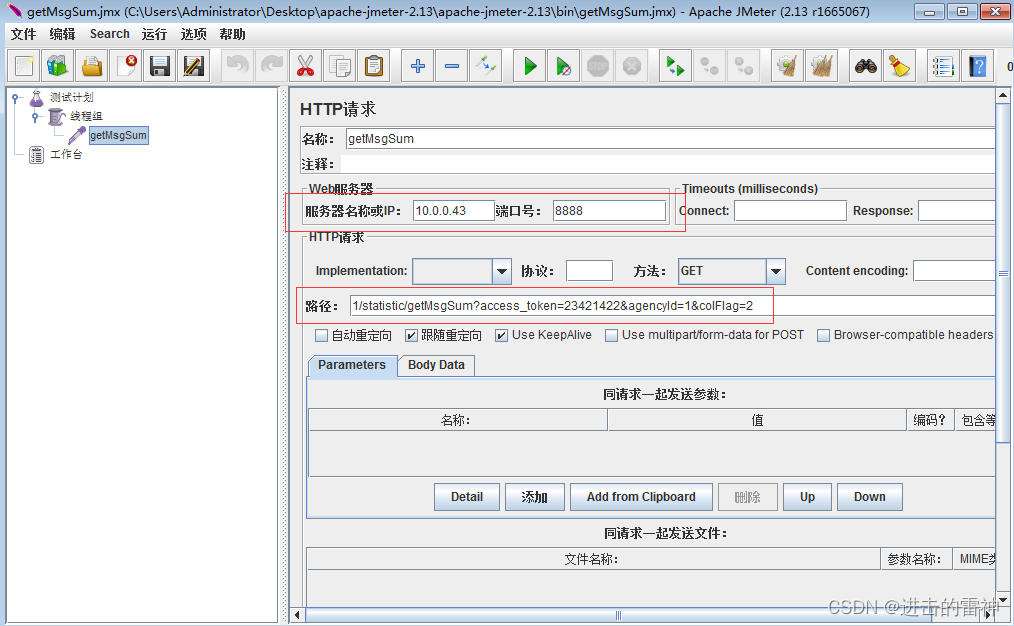
第4步，给请求参数化，这里选择agencyId参数化，首先在本地创建一个文件，这里创建了一个命名为param.txt的文件，编辑该文件输入参数化值，如下图

 

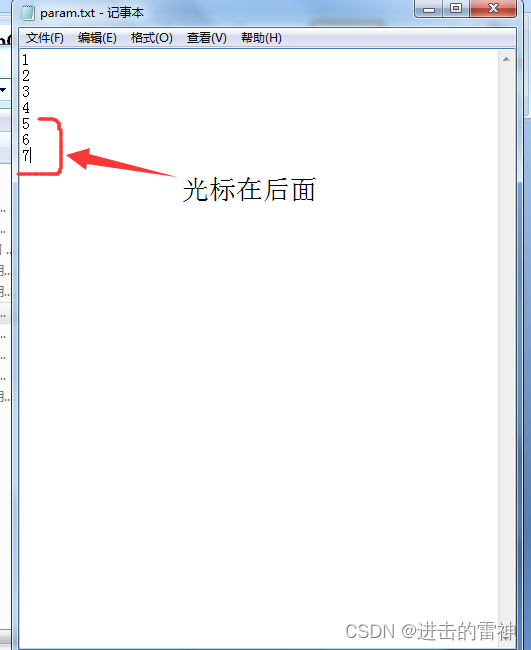
创建一个CSV Data Set Config, 并配置如下图

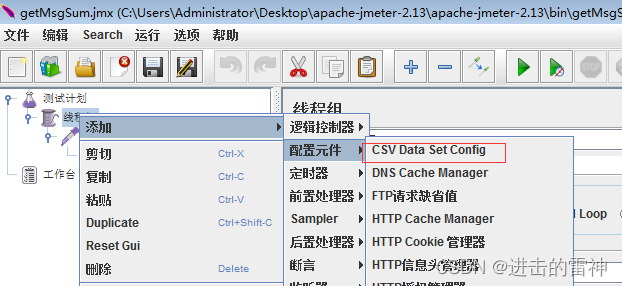
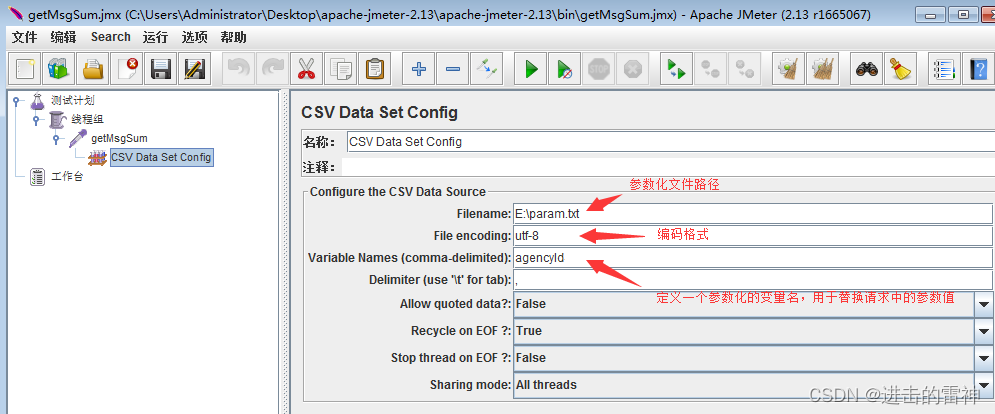
将agencyId=1 的1替换为${agencyId}，这里要注意，不能漏掉 $ 符号

第5步设置线程组中的参数，为了实现多用户并发测试

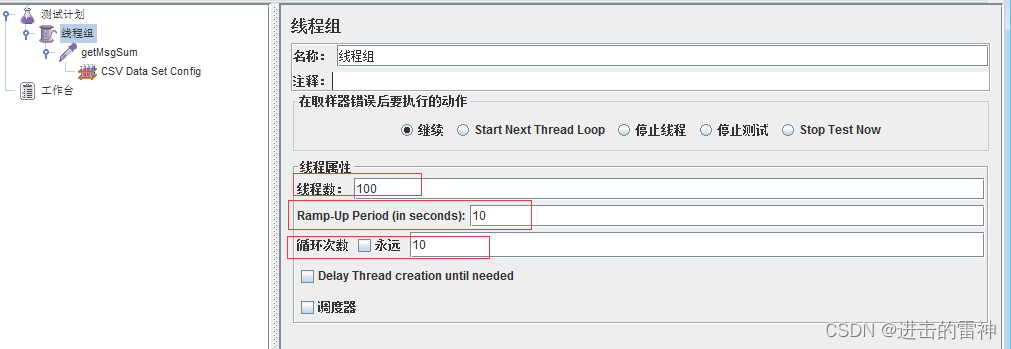
线程数: 一个用户占一个线程， 100个线程就是模拟100个用户

Ramp-Up Period(in seconds): 设置线程需要多长时间全部启动。如果线程数为100 ，准备时长为10 ，那么需要1秒钟启动10个线程。也就是每秒钟启动10个线程。

循环次数: 每个线程发送请求的次数。如果线程数为100 ，循环次数为10 ，那么每个线程发送10次请求。总请求数为100*10=1000 。如果勾选了“永远”，那么所有线程会一直发送请求，直到选择停止运行脚本。

设置启动时间：

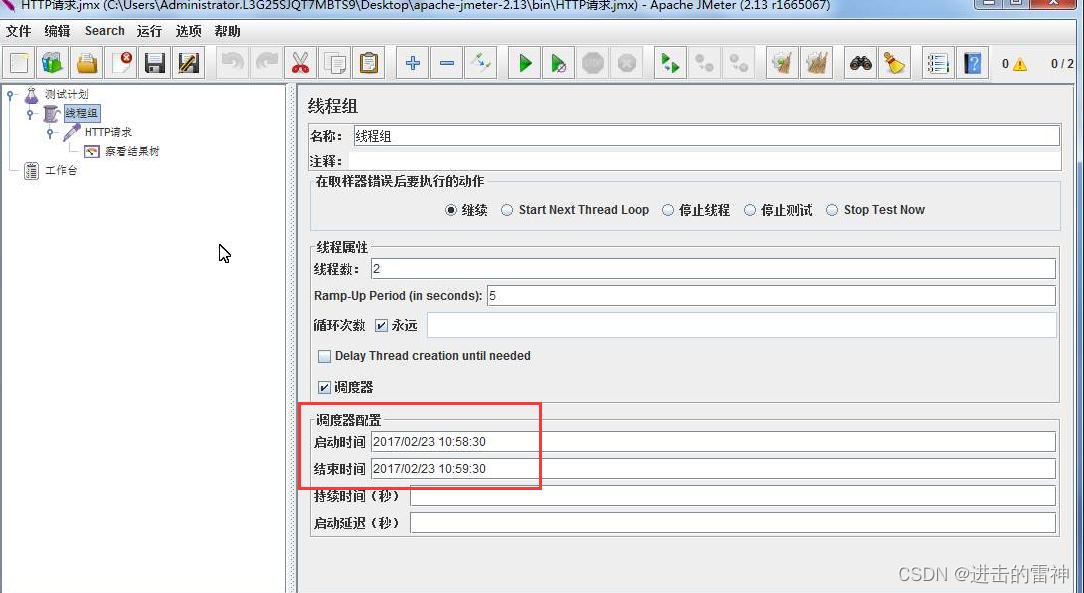
第6步，添加查看结果树和聚合报告

第7步，查看聚合报告，收集接口性能测试结果

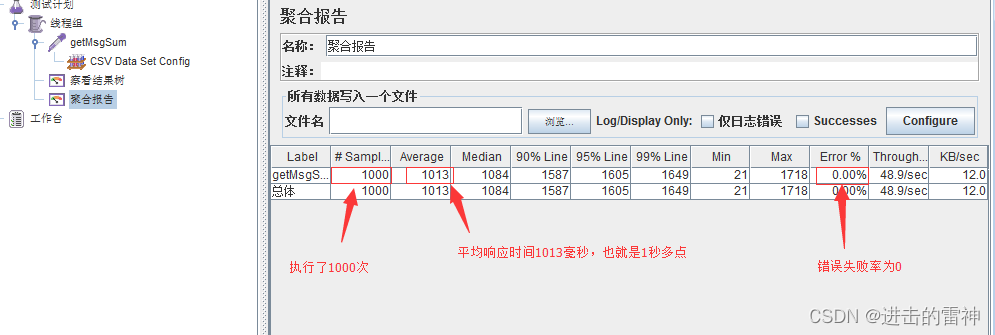
第8步，添加图形结果，收集接口性能测试曲线图

图略