目录

第一题

题目来源

题目内容

解决方法

方法一：双指针

方法二：递归

方式三：迭代

方法四：优先队列

第二题

题目来源

题目内容

解决方法

方法一：贪心算法

方法二：数学方法

方法三：递归算法

第三题

题目来源

题目内容

解决方法

方法一：回溯法

方法二：动态规划

方法三：栈

方法四：暴力法

---

第一题

题目来源

21. 合并两个有序链表 - 力扣（LeetCode）

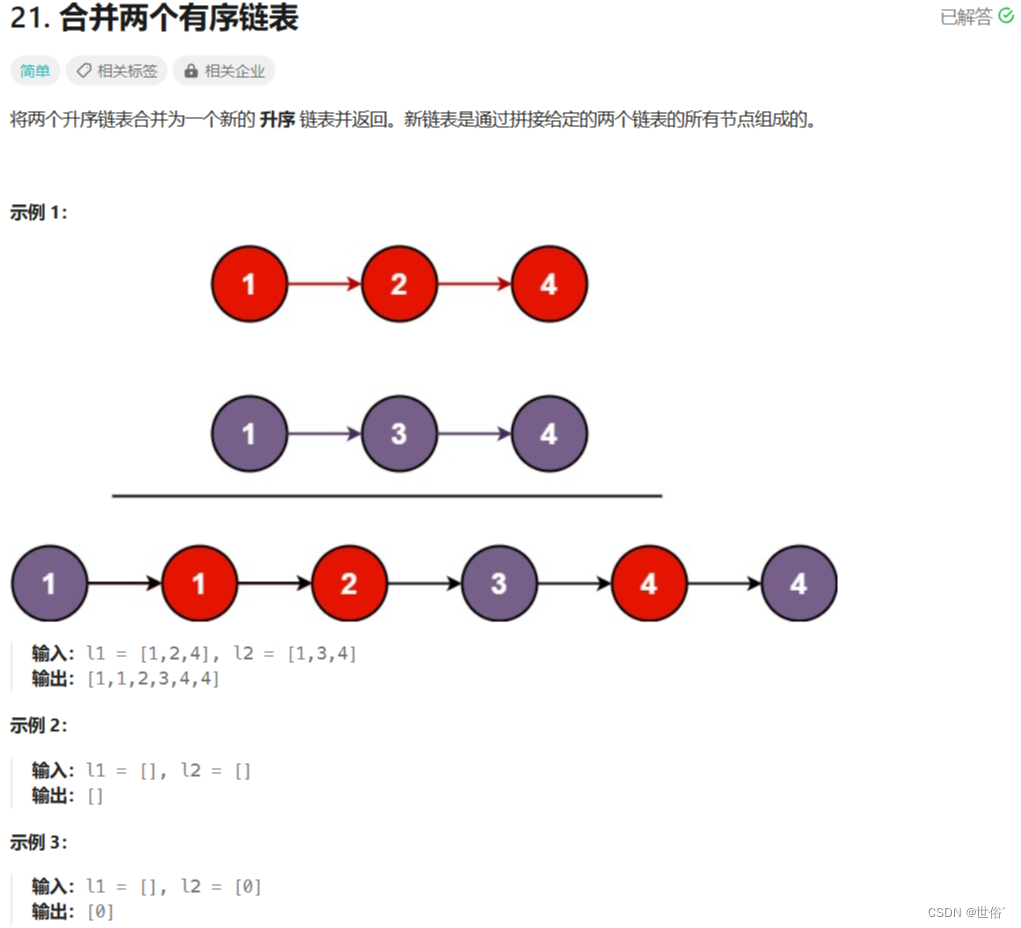
题目内容

解决方法

方法一：双指针

由于题目要求合并两个升序链表，并且新链表也要按照升序排列，因此我们可以使用双指针的方法，依次比较两个链表的结点值大小，将较小的结点接在新链表的最后面。

具体来讲，在遍历两个链表的过程中，我们可以维护一个指针cur，它指向新链表的当前最后一个结点。对于每个结点值比较小的链表，我们就将它的结点接在cur结点的后面，并将cur指针后移，继续比较。当其中一个链表为空时，说明没有可以比较的结点了，我们将另一个链表的剩余结点全部接在新链表的最后面。最后返回新链表的第一个有效结点即可。

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(-1); // 新链表的虚拟头结点
        ListNode cur = dummy; // cur指向当前新链表的最后一个结点

        while (l1 != null && l2 != null) {
            if (l1.val <= l2.val) { // l1结点的值比较小
                cur.next = l1; // 将l1的结点接在当前新链表的最后一个结点后面
                l1 = l1.next; // 指针后移
            } else { // l2结点的值比较小
                cur.next = l2; // 将l2的结点接在当前新链表的最后一个结点后面
                l2 = l2.next; // 指针后移
            }
            cur = cur.next; // 指针后移
        }

        // l1或者l2还有剩余结点，将它们全部接到新链表的最后一个结点后面
        if (l1 != null) {
            cur.next = l1;
        } else if (l2 != null) {
            cur.next = l2;
        }

        return dummy.next; // 返回新链表的第一个有效结点
    }
}

复杂度分析：

• 在这个解法中，我们需要遍历两个链表并依次比较结点值，然后将小的结点接在新链表的最后面。因此，时间复杂度是O(m+n)，其中m和n分别是两个链表的长度。
• 空间复杂度是O(1)，因为只需要常数级别的额外空间来存储指针变量。

需要注意的是：这里的时间复杂度是线性的，而不是二次的，因为我们每次都只移动一个链表的指针，而不是将所有结点都拷贝到新链表中。因此，这个解法是非常高效的。

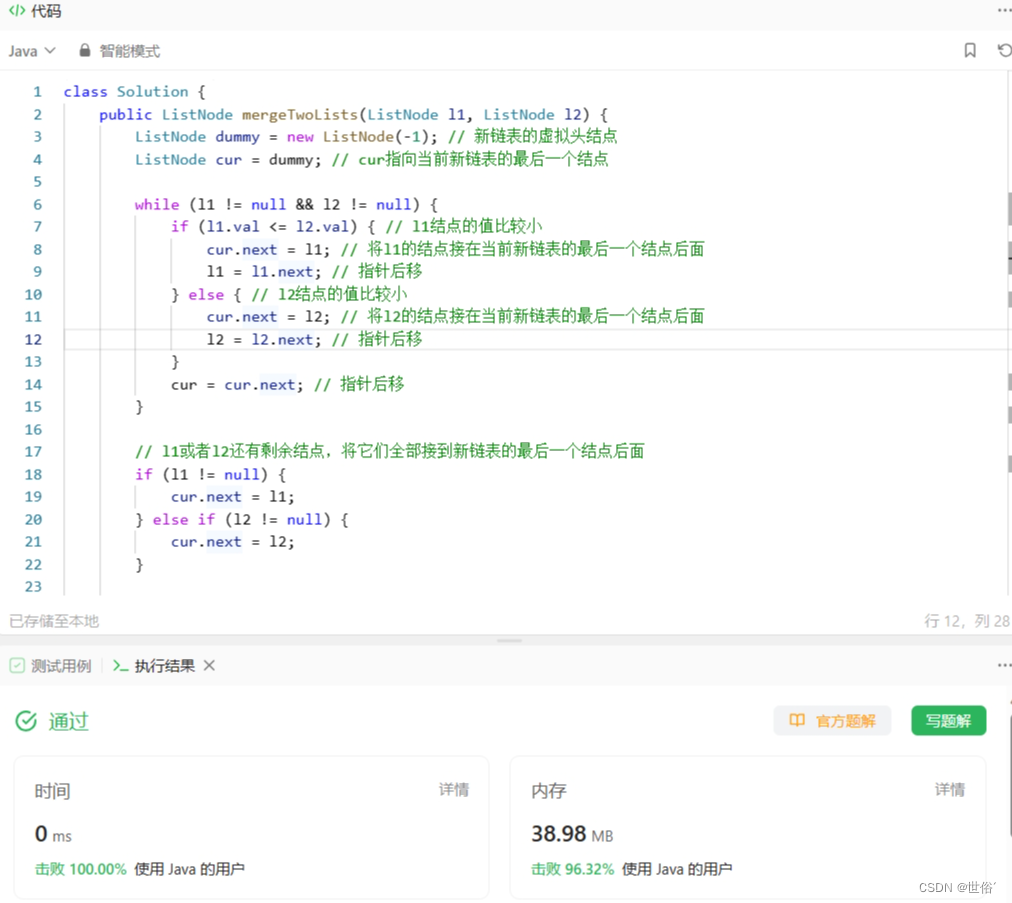
LeetCode运行结果：

方法二：递归

除了使用双指针比较的方法外，还可以考虑使用递归实现合并两个升序链表的操作。

递归的思路是，对于两个链表l1和l2，我们比较它们的头结点的值，将较小的头结点作为新链表的头结点，并递归地处理剩余的结点，直到其中一个链表为空。然后，将另一个链表的剩余部分直接接到新链表的末尾。

具体来说，我们定义一个递归函数mergeLists(l1, l2)来处理两个链表的合并操作：

• 如果其中一个链表为空，说明已经没有可以合并的结点了，直接返回另一个非空的链表。
• 否则，比较两个链表的头结点值，将较小的头结点作为新链表的头结点，然后递归地调用mergeLists()函数来处理剩余的结点，并将返回的结果接在新链表的头结点后面。

递归终止条件是当两个链表都为空时，返回空链表。

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        // 递归终止条件：其中一个链表为空
        if (l1 == null || l2 == null) {
            return l1 != null ? l1 : l2; 
        }
        // 比较两个链表的头结点值
        else if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2); // 递归处理剩余结点
            return l1;// 返回新链表的头结点
        }
        else {
            l2.next = mergeTwoLists(l1, l2.next);// 递归处理剩余结点
            return l2;// 返回新链表的头结点
        }
    }
}

复杂度分析：

时间复杂度分析：

• 每次递归调用都会处理其中一个链表的头节点，并将问题规模缩减为规模较小的子问题。
• 在每次递归调用中，我们只处理一个节点，而且每个节点至多只会被访问一次。
• 因此，递归方法的总时间复杂度是O(m+n)，其中m和n分别是两个链表的长度。

空间复杂度分析：

• 递归方法的空间复杂度取决于递归调用的深度。
• 在最坏情况下，如果链表l1和l2的长度之和为m+n，并且所有的节点都是递归调用栈中的活动状态，则递归的最大深度为m+n。
• 因此，递归方法的总空间复杂度是O(m+n)。

总结：递归方法的时间复杂度是O(m+n)，空间复杂度是O(m+n)。

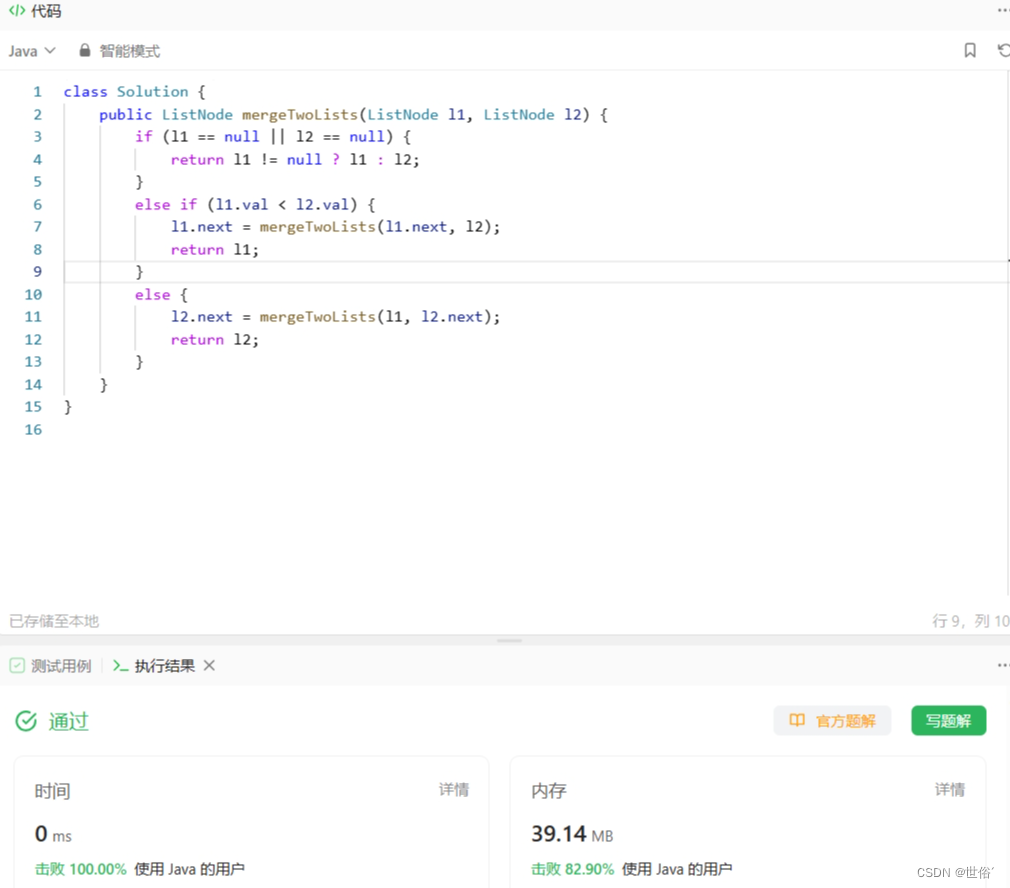
LeetCode运行结果：

方式三：迭代

除了使用递归和双指针的方法外，还可以使用迭代的方式来合并两个升序链表。

迭代的思路是，我们创建一个新的链表，用来存储合并后的结果。然后我们使用两个指针分别指向两个链表的头节点，比较两个节点的值，将较小的节点添加到新链表中，并将相应的指针后移一位，直到其中一个链表遍历完毕。最后，将剩余部分的链表直接接到新链表的末尾。

具体来说，我们定义三个指针：dummy指向新链表的头节点，curr指向新链表的当前节点，p1和p2分别指向两个链表的当前节点。初始时，将dummy和curr都指向一个虚拟的头节点，p1指向链表l1的头节点，p2指向链表l2的头节点。

然后，我们进行循环比较操作：

• 如果p1指向的节点的值小于等于p2指向的节点的值，将p1指向的节点接入新链表，p1后移一位；
• 否则，将p2指向的节点接入新链表，p2后移一位。

每次操作完成后，curr指针和被接入节点都后移一位。

循环终止时，其中一个链表已经遍历完毕。如果另一个链表还有剩余节点，则将剩余部分直接接入新链表的末尾。

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(0); // 虚拟头节点
        ListNode curr = dummy; // 当前节点
        ListNode p1 = l1; // 链表l1的当前节点
        ListNode p2 = l2; // 链表l2的当前节点
        
        // 循环比较操作
        while (p1 != null && p2 != null) {
            if (p1.val <= p2.val) {
                curr.next = p1;
                p1 = p1.next;
            } else {
                curr.next = p2;
                p2 = p2.next;
            }
            curr = curr.next;
        }
        
        // 将剩余部分直接接入新链表的末尾
        curr.next = (p1 != null) ? p1 : p2;
        
        return dummy.next; // 返回新链表的头节点
    }
}

复杂度分析：

• 使用迭代方法合并两个升序链表的时间复杂度是O(m+n)，其中m和n分别是两个链表的长度。这是因为我们需要遍历两个链表中的所有节点，并比较节点的值。
• 空间复杂度是O(1)，因为我们只使用了常数级别的额外空间来存储指针和临时变量，不随输入规模的增加而增加。

总结：迭代方法的时间复杂度是O(m+n)，空间复杂度是O(1)。与递归方法相比，迭代方法具有相同的时间复杂度，但空间复杂度更低。

LeetCode运行结果：

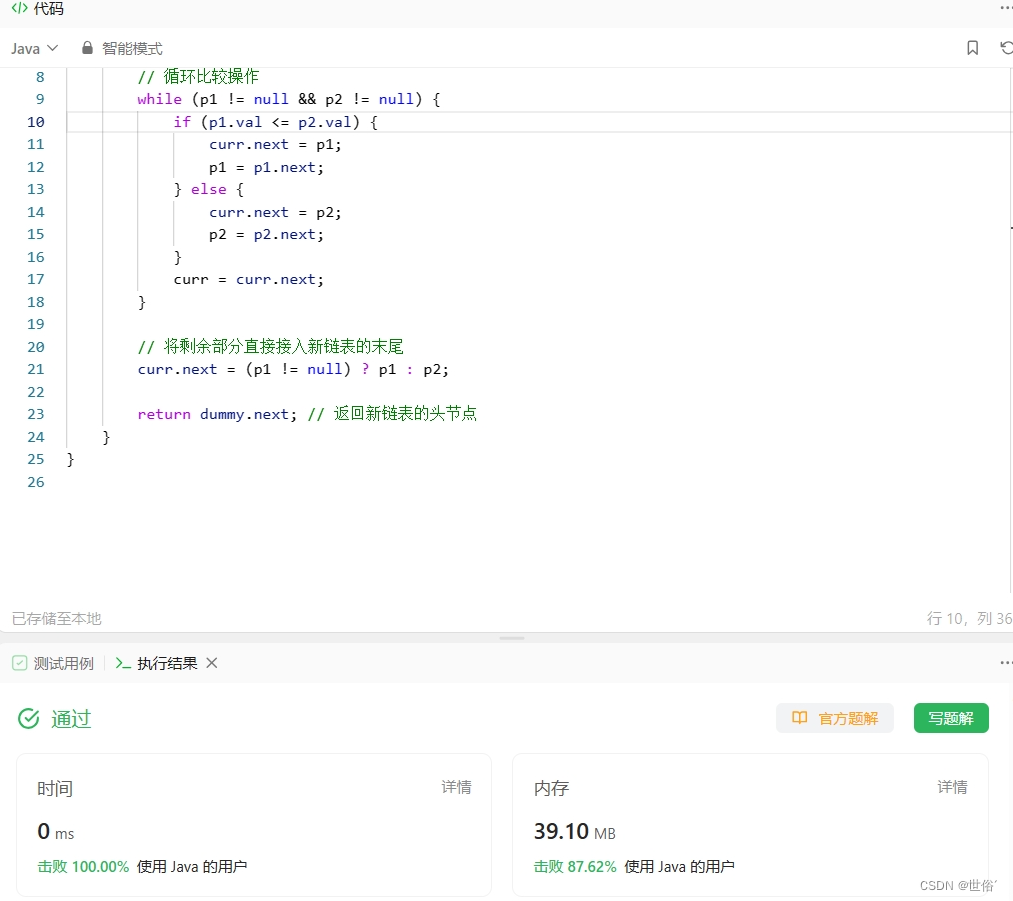
方法四：优先队列

除了递归和迭代方法外，还有一种另类思路，可以使用优先队列（Priority Queue）来实现合并两个升序链表。

具体操作如下：

1. 创建一个空的优先队列，设置比较器为链表节点值的大小，即小根堆；
2. 将两个链表的所有节点依次加入优先队列中；
3. 从优先队列中不断取出最小值（即堆顶元素），将其接入新链表；
4. 重复步骤3，直到优先队列为空。

这种思路在理论上是可行的，因为小根堆可以始终保证堆顶元素是当前所有元素的最小值。而对于每个链表中的节点，只需要依次入堆一次，出堆一次，时间复杂度都是O(log(m+n))，由于共有m+n个节点，因此总时间复杂度是O((m+n)log(m+n))。

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        PriorityQueue<ListNode> pq = new PriorityQueue<>((a, b) -> a.val - b.val);
        ListNode dummy = new ListNode(0), curr = dummy;
        
        // 将两个链表的所有节点依次加入优先队列中
        if (l1 != null) pq.offer(l1);
        if (l2 != null) pq.offer(l2);
        
        while (!pq.isEmpty()) {
            ListNode node = pq.poll(); // 取出最小值
            curr.next = node; // 加入新链表
            curr = curr.next; // 当前节点后移
            
            if (node.next != null) {
                pq.offer(node.next); // 将该元素所属的链表中的下一个节点入堆
            }
        }
        
        return dummy.next; // 返回新链表的头节点
    }
}

复杂度分析：

• 使用优先队列方法合并两个升序链表的时间复杂度是O((m+n)log(m+n))，其中m和n分别是两个链表的长度。这是因为我们需要将所有节点依次加入优先队列中，每次插入操作的时间复杂度是O(log(m+n))，而插入操作需要执行m+n次。
• 空间复杂度是O(m+n)，因为优先队列需要存储所有节点，最坏情况下有m+n个节点。

总结：使用优先队列的方法可以实现合并两个升序链表，但时间复杂度较高，为O((m+n)log(m+n))，空间复杂度为O(m+n)。这种方法在实践中并不是最优解，相比之下，递归和迭代方法更为简洁、高效。

LeetCode运行结果：

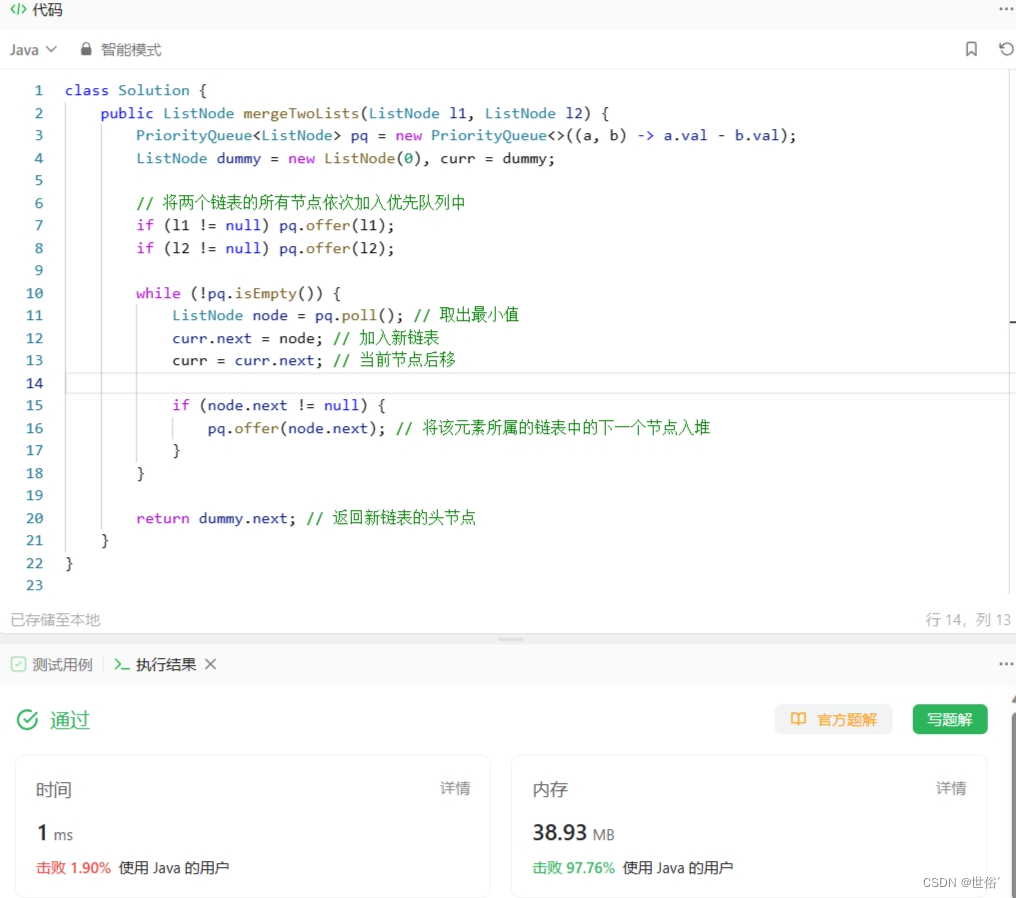
第二题

题目来源

LCP 06. 拿硬币 - 力扣（LeetCode）

题目内容

解决方法

方法一：贪心算法

我们可以通过贪心算法来解决这个问题。

具体步骤如下：

1、遍历数组 coins，对于每一堆力扣币：

• 如果该堆力扣币数量是偶数，则只需要拿 coins[i] / 2 次；
• 如果该堆力扣币数量是奇数，则需要拿 (coins[i] / 2) + 1 次。

2、将每一堆力扣币所需的次数累加，得到总的最少次数。

class Solution {
    public int minCount(int[] coins) {
        int count = 0;
        for (int i = 0; i < coins.length; i++) {
            if (coins[i] % 2 == 0) {
                count += coins[i] / 2;
            } else {
                count += coins[i] / 2 + 1;
            }
        }
        return count;
    }
}

复杂度分析：

• 这种方法的时间复杂度为 O(n)，其中 n 是数组 coins 的长度。
• 由于每堆力扣币只需要计算一次，因此空间复杂度是 O(1)。

注意：这种贪心算法仅适用于给定的限制条件，即力扣币数量较小。如果力扣币数量较大，或者限制条件有所改变，可能需要使用其他算法来解决。

LeetCode运行结果：

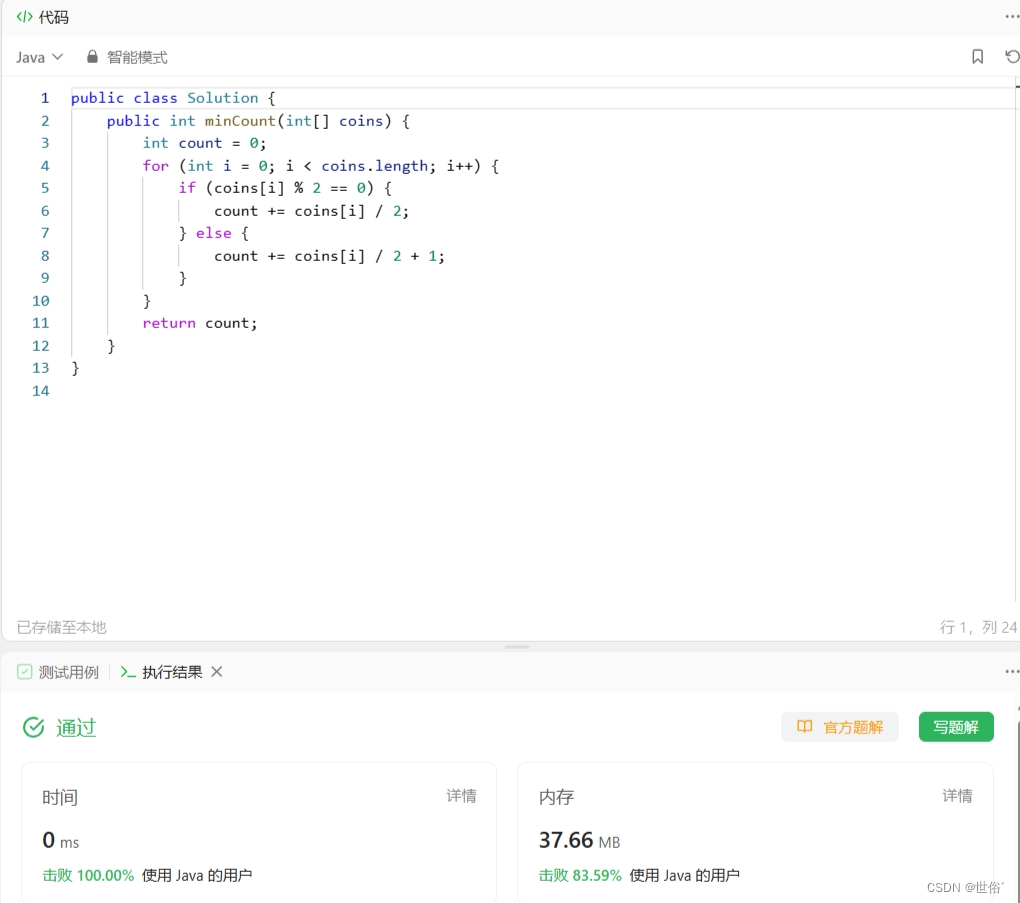
方法二：数学方法

还可以考虑利用数学方法来解决这个问题。

观察到题目中只有两种操作：拿取一枚力扣币（计数为1）和拿取两枚力扣币（计数为2）。我们可以将每堆力扣币按拿取两枚力扣币的方式进行分组，即将余数为0的力扣币堆直接计数为拿取两枚力扣币的次数。然后，再统计余数为1的力扣币堆，每堆需要额外拿取一枚力扣币，将其计数为拿取两枚力扣币的次数，并将拿取一枚力扣币的次数加1。通过这种方法，可以直接得到最少的拿取次数。

class Solution {
    public int minCount(int[] coins) {
        int count = 0;
        
        for (int i = 0; i < coins.length; i++) {
            count += coins[i] / 2; // 余数为0的力扣币堆直接计数为拿取两枚力扣币的次数
            if (coins[i] % 2 != 0) {
                count++; // 余数为1的力扣币堆需要额外拿取一枚力扣币
            }
        }
        
        return count;
    }
}

复杂度分析：

• 时间复杂度：该算法只需要遍历力扣币数组一次，时间复杂度为 O(N)，其中 N 是力扣币的数量。
• 空间复杂度：该算法只使用了常量级的额外空间，空间复杂度为 O(1)。

因此，使用数学方法解决该问题的算法复杂度较低，是一种高效的解决方案。

LeetCode运行结果：

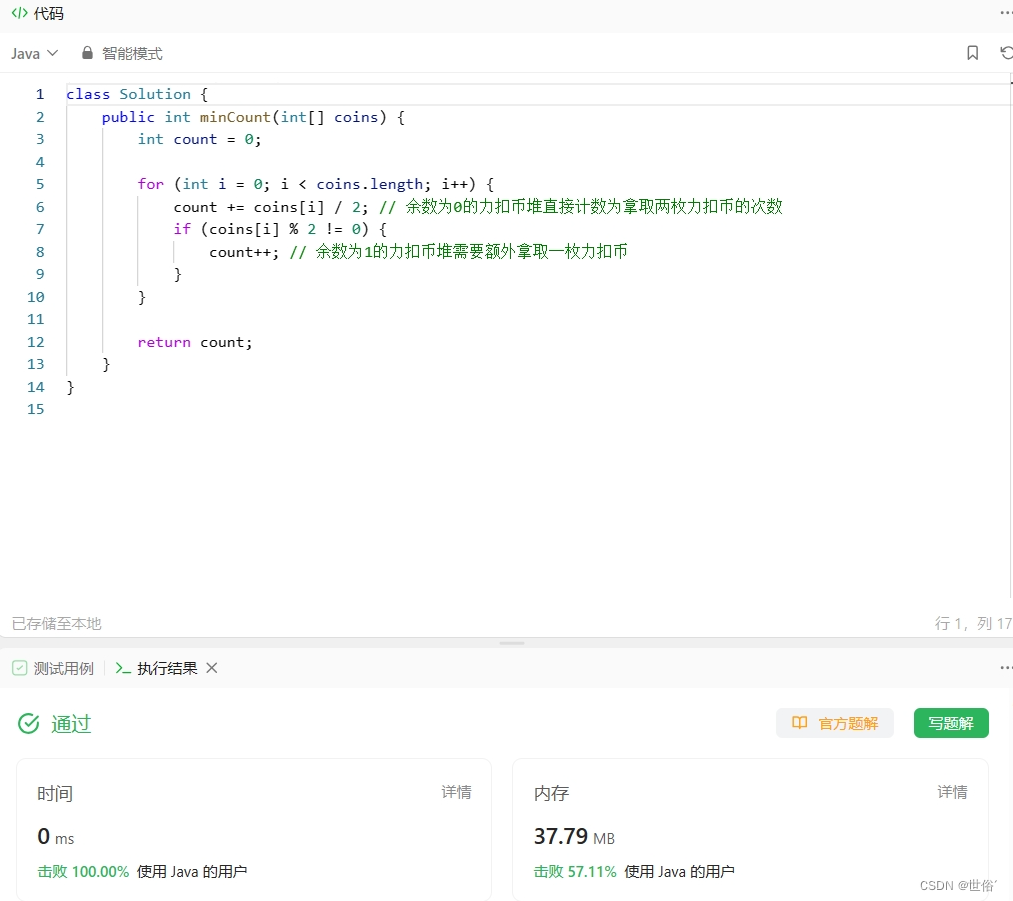
方法三：递归算法

public class Solution {
    public int minCount(int[] coins) {
        int count = 0;
        for (int coin : coins) {
            count += getCoinCount(coin);
        }
        return count;
    }

    private int getCoinCount(int coinNum) {
        if (coinNum == 0) {
            return 0;
        }
        if (coinNum <= 2) {
            return 1; // 如果只有1或2个力扣币，则最少拿取1次
        }
        if (coinNum % 2 == 0) {
            return coinNum / 2; // 如果力扣币数能够被2整除，尽量拿取2枚力扣币
        } else {
            return (coinNum / 2) + 1; // 如果力扣币数不能被2整除，则需要额外拿取1枚力扣币
        }
    }
}

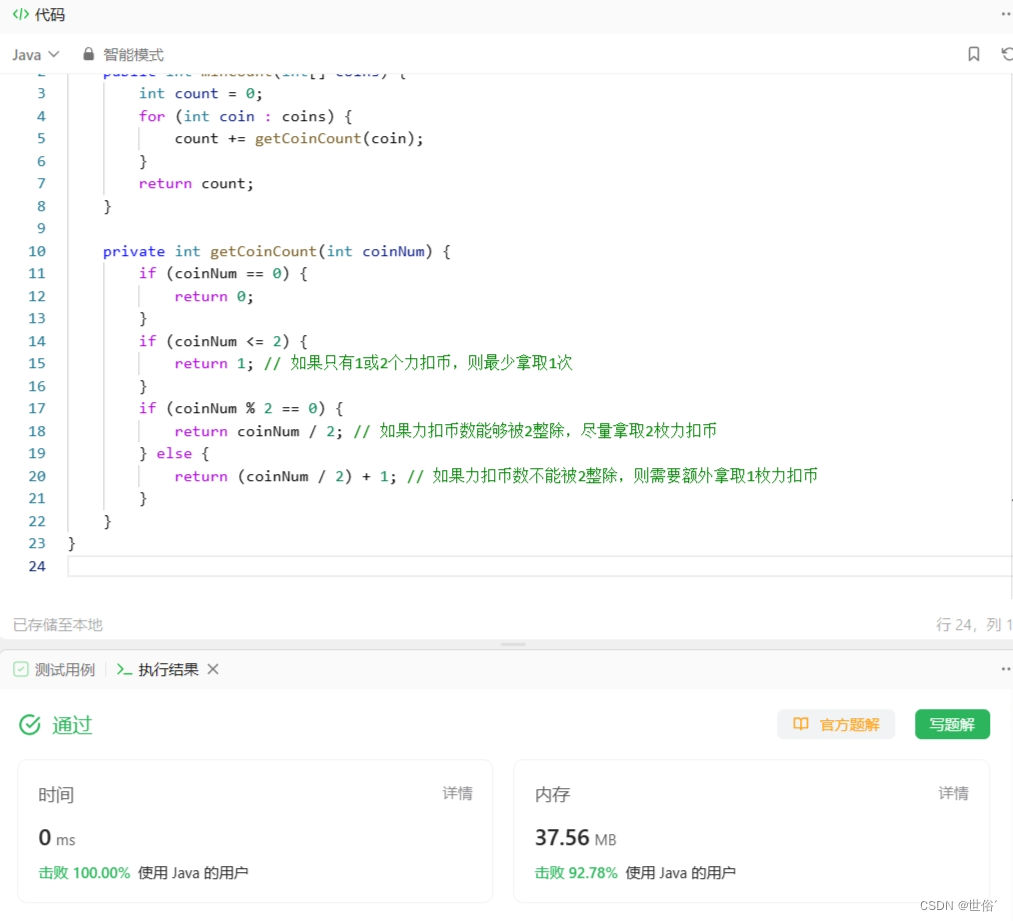
这个代码实现使用了递归的思路，每次递归的时候判断剩余的力扣币数量，并根据剩余数量选择拿取1枚力扣币或2枚力扣币。在递归过程中计算拿取次数直到剩余的力扣币数量为0为止。

详细地说，如果剩余的力扣币数量为0，则返回0；如果剩余的力扣币数量只有1或2个，则返回1；如果剩余的力扣币数量可以被2整除，则尽量拿取2枚力扣币；否则，就要额外拿取1枚力扣币。

复杂度分析：

• 该递归算法的时间复杂度为指数级别，具体地说是 O(2^N)，其中 N 是力扣币的数量。
• 空间复杂度为 O(N)，用于存储递归栈中的信息。

虽然在时间复杂度方面不如其他算法效率高，但是它实现简单易懂，应对一些简单的场景也是完全可以的。

LeetCode运行结果：

第三题

题目来源

22. 括号生成 - 力扣（LeetCode）

题目内容

解决方法

方法一：回溯法

要生成有效的括号组合，可以使用回溯法来解决这个问题。在回溯过程中，需要维护左括号和右括号的数量，并根据一定的条件进行剪枝。

import java.util.ArrayList;
import java.util.List;

public class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> result = new ArrayList<>();
        backtrack(result, "", 0, 0, n);
        return result;
    }

    private void backtrack(List<String> result, String current, int leftCount, int rightCount, int n) {
        if (current.length() == n * 2) {
            result.add(current);
            return;
        }

        if (leftCount < n) {
            backtrack(result, current + "(", leftCount + 1, rightCount, n);
        }

        if (rightCount < leftCount) {
            backtrack(result, current + ")", leftCount, rightCount + 1, n);
        }
    }
}

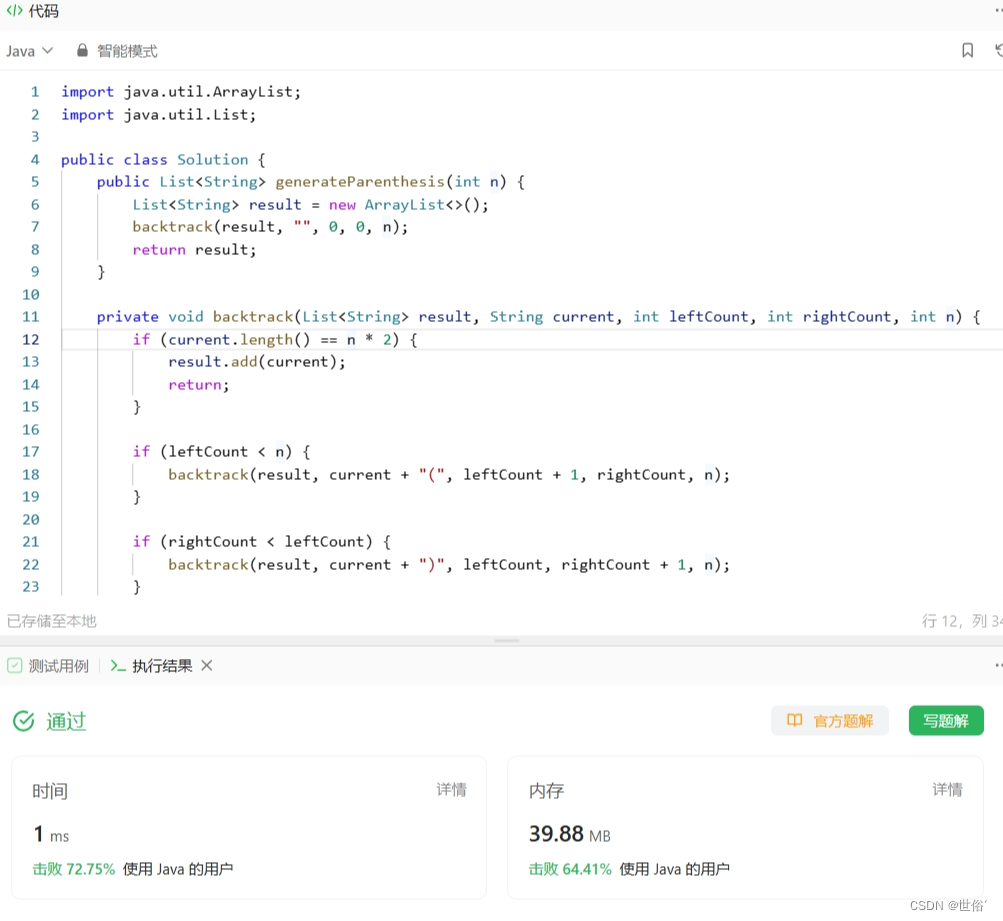
在这个代码中，generateParenthesis 方法接收一个整数 n，代表括号的对数，返回一个包含所有可能的且有效的括号组合的列表。backtrack 方法用于进行回溯。它维护了一个当前的字符串 current，其中 leftCount 和 rightCount 分别表示当前已使用的左括号和右括号的数量。n 则表示要生成的括号对数。在回溯过程中，如果当前字符串的长度达到了 n*2，就代表已经生成了一个有效的括号组合，将其添加到结果列表中。然后，通过递归调用 backtrack 方法，分别尝试放置左括号和右括号。在放置左括号时，需要判断已使用的左括号数量是否小于 n，如果是，则可以继续放置左括号。在放置右括号时，需要判断已使用的右括号数量是否小于左括号数量，如果是，则可以继续放置右括号。通过不断进行递归调用和回溯，最终可以得到所有可能的且有效的括号组合。

复杂度分析：

时间复杂度：

• 回溯算法的时间复杂度一般是指数级别的。
• 在每个位置上，我们有两种选择：放置左括号或放置右括号。
• 递归的深度是 2n，因为在一个有效的括号组合中，左括号和右括号的数量都是 n。
• 每个递归层级的操作是常数时间。
• 因此，总时间复杂度为 O(2^2n)，即指数级别。

空间复杂度：

• 在回溯算法中，需要维护一个字符串 current 存储当前的括号组合，字符串的长度最大为 2n。
• 使用递归调用时会出现最多 2n 个递归层级。
• 因此，总空间复杂度为 O(2n)，即线性级别。

综上所述，生成有效括号组合的函数的时间复杂度为指数级别的 O(2^2n)，空间复杂度为线性级别的 O(2n)。

LeetCode运行结果：

方法二：动态规划

除了回溯法外，还可以使用动态规划来生成有效括号组合。

import java.util.ArrayList;
import java.util.List;

public class Solution {
    public List<String> generateParenthesis(int n) {
        List<List<String>> dp = new ArrayList<>();
        dp.add(new ArrayList<>());
        dp.get(0).add("");

        for (int i = 1; i <= n; i++) {
            List<String> current = new ArrayList<>();

            for (int j = 0; j < i; j++) {
                List<String> inside = dp.get(j);
                List<String> outside = dp.get(i - j - 1);

                for (String in : inside) {
                    for (String out : outside) {
                        current.add("(" + in + ")" + out);
                    }
                }
            }

            dp.add(current);
        }

        return dp.get(n);
    }
}

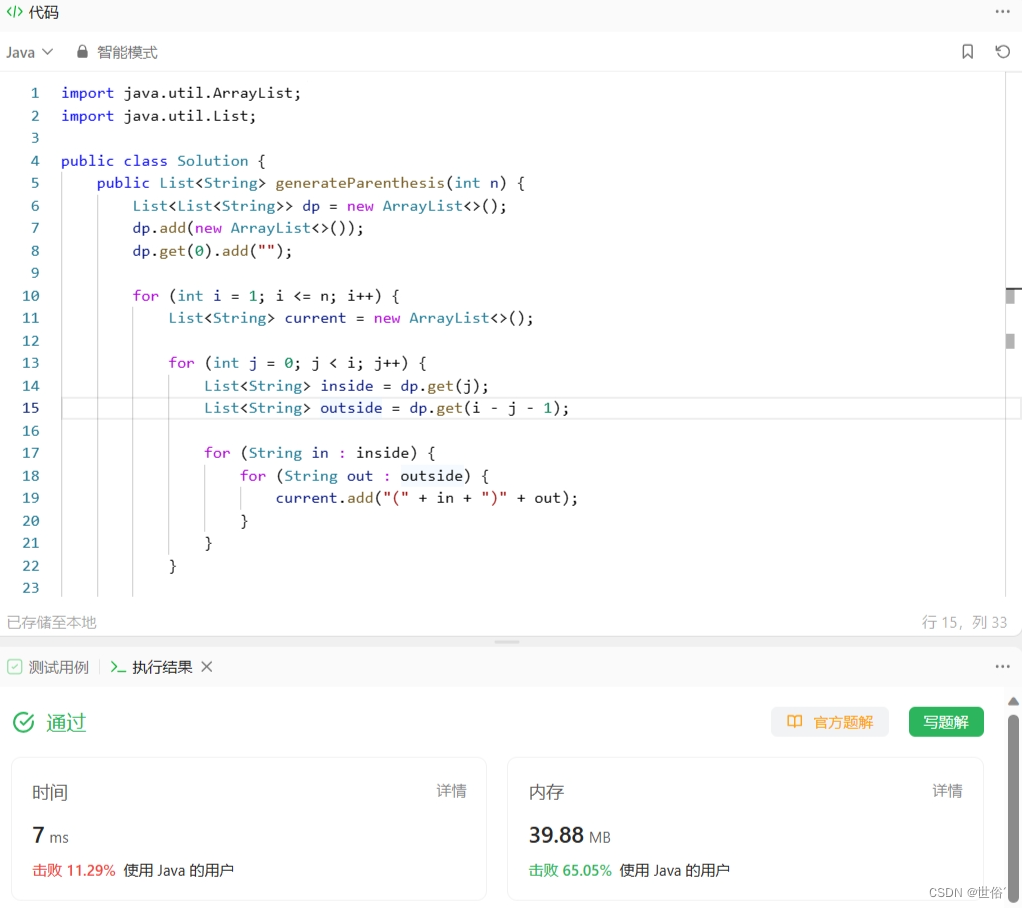
1. 在这个代码中，我们使用一个二维列表 dp 来存储每个括号对数对应的括号组合列表。dp[i] 表示使用 i 个括号对所能生成的所有有效括号组合。其中 dp[0] 是一个空列表。
2. 接下来，我们通过动态规划的方式从 dp[0] 开始逐步计算 dp[n]，直到得到 dp[n] 的结果。
3. 对于每个 dp[i]，我们迭代遍历 j 从 0 到 i-1，找到当前括号对数 i 的所有可能的括号对数分配，即左括号对数 j 和右括号对数 i-j-1。
4. 然后，将括号对数为 j 的组合和括号对数为 i-j-1 的组合进行组合，得到当前 dp[i] 的所有组合。
5. 最后，将计算结果 dp[n] 返回作为最终的结果列表。

复杂度分析：

时间复杂度：

• 在每个位置上，我们需要计算当前括号对数 i 的所有可能组合。
• 对于每个 i，我们需要迭代遍历 j 从 0 到 i-1。
• 在每个迭代步骤中，我们需要将两个组合进行组合，这些组合的数量与它们的长度成正比。
• 因此，总时间复杂度为 O(n^2 * Cn)，其中 Cn 是括号组合的数量。

空间复杂度：

• 我们使用一个二维列表 dp 来存储每个括号对数对应的括号组合列表。
• 二维列表 dp 的大小为 (n+1) x m，其中 n 是括号对数，m 是平均每个括号组合的长度。
• 因此，总空间复杂度为 O(n * m)。

需要注意的是，具体括号组合的数量取决于具体的 n。在某些情况下，括号组合的数量可能大于 2^n，因此花费的时间和空间可能会更多。

综上所述，使用动态规划生成有效括号组合的函数的时间复杂度为 O(n^2 * Cn)，空间复杂度为 O(n * m)。

LeetCode运行结果：

方法三：栈

我们使用栈来模拟括号的匹配过程。

1、在回溯函数 backtrack 中，我们维护两个计数器 open 和 close，分别表示当前已经使用的左括号和右括号的个数。

2、如果栈的大小达到了 2n（n 是括号对数），说明已经得到了一个有效的括号组合，将其转换为字符串并添加到结果列表中。

否则，我们有两种选择：

• 如果左括号的个数 open 小于 n，可以将一个左括号压入栈中，并递归调用 backtrack。
• 如果右括号的个数 close 小于左括号的个数 open，可以将一个右括号压入栈中，并递归调用 backtrack。

3、每次递归调用结束后，我们需要将栈顶元素弹出，以便进行下一次选择。

4、通过不断选择和回溯，最终得到所有可能的有效括号组合。

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> result = new ArrayList<>();
        backtrack(result, new Stack<Character>(), 0, 0, n);
        return result;
    }

    private void backtrack(List<String> result, Stack<Character> stack, int open, int close, int n) {
        if (stack.size() == 2 * n) {
            StringBuilder sb = new StringBuilder();
            for (char c : stack) {
                sb.append(c);
            }
            result.add(sb.toString());
            return;
        }

        if (open < n) {
            stack.push('(');
            backtrack(result, stack, open + 1, close, n);
            stack.pop();
        }

        if (close < open) {
            stack.push(')');
            backtrack(result, stack, open, close + 1, n);
            stack.pop();
        }
    }
}

复杂度分析：

• 时间复杂度分析： 在回溯过程中，每次我们有两种选择：添加左括号或者添加右括号。因此，总共的递归调用次数为 2^(2n)，其中 n 是括号对数。每次递归调用都会将一个字符压入栈中或弹出栈顶字符，这些操作的时间复杂度为 O(1)。因此，总体的时间复杂度为 O(2^(2n) * 1) = O(2^(2n))。
• 空间复杂度分析： 在回溯过程中，我们使用了一个栈来模拟括号的匹配过程。栈中最多存放 2n 个字符（左括号和右括号），因此栈的空间复杂度为 O(2n) = O(n)。此外，我们还需要用一个 StringBuilder 来构建结果字符串，其空间复杂度也为 O(n)。因此，总体的空间复杂度为 O(n)。

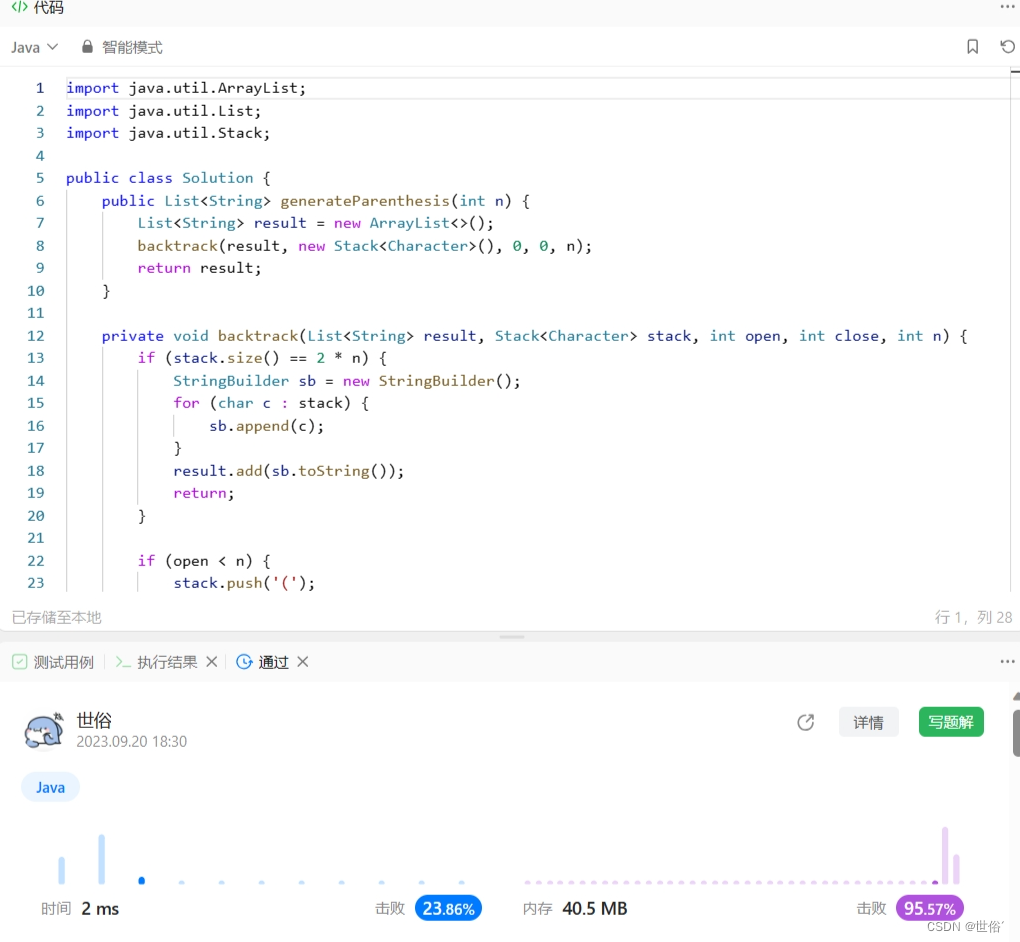
综上所述，使用栈的解决方案的时间复杂度为 O(2^(2n))，空间复杂度为 O(n)。

LeetCode运行结果：

方法四：暴力法

当括号对数较小（例如，n <= 8）时，我们可以使用暴力法生成所有可能的括号组合。暴力法的思路是通过递归生成所有可能的组合，然后检查它们是否有效。

1. 我们使用一个字符数组 current 来记录当前正在生成的括号组合，该数组的长度为 2 * n，即括号对数的两倍。
2. 我们通过递归的方式生成所有可能的括号组合。在每一步递归中，我们可以选择放置一个左括号或一个右括号。递归的终止条件是当 pos 等于 current.length 时，即所有位置都已经填满。然后，我们检查当前组合是否有效（即括号是否匹配），如果有效，则将其加入到结果列表 result 中。
3. 在判断括号组合是否有效的方法 isValid 中，我们使用了一个变量 balance 来记录左右括号的平衡情况。遍历数组 current，如果遇到左括号则增加 balance，如果遇到右括号则减少 balance。如果 balance 为负数，则说明右括号数量大于左括号数量，这种情况下括号组合无效。

import java.util.ArrayList;
import java.util.List;

public class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> combinations = new ArrayList<>();
        generateAll(new char[2 * n], 0, combinations);
        return combinations;
    }

    private void generateAll(char[] current, int pos, List<String> result) {
        if (pos == current.length) {
            if (isValid(current)) {
                result.add(new String(current));
            }
        } else {
            current[pos] = '(';
            generateAll(current, pos + 1, result);
            current[pos] = ')';
            generateAll(current, pos + 1, result);
        }
    }

    private boolean isValid(char[] current) {
        int balance = 0;
        for (char c : current) {
            if (c == '(') {
                balance++;
            } else {
                balance--;
                if (balance < 0) {
                    return false;
                }
            }
        }
        return balance == 0;
    }
}

复杂度分析：

时间复杂度分析：

• 生成所有可能的括号组合需要考虑的情况共有 2^(2n) 种，其中每个位置可以放置左括号或右括号两种选择，总共有 2^(2n) 种组合。
• 对于每个组合，我们需要进行有效性检查，即检查括号是否匹配，需要遍历组合中的字符，因此时间复杂度为 O(n)。
• 综上所述，暴力法的时间复杂度为 O(2^(2n) * n)。

空间复杂度分析：

• 暴力法中使用了一个字符数组 current 来保存当前正在生成的括号组合，数组长度为 2 * n。
• 递归过程中每一层都会创建一个新的字符数组，因此递归的最大深度是 n，因此空间复杂度为 O(n)。
• 在结果列表 result 中存储了所有可能的括号组合，最坏情况下有 2^(2n) 个组合，每个组合的平均长度为 2 * n，因此空间复杂度为 O(2^(2n) * n)。
• 综上所述，暴力法的空间复杂度为 O(2^(2n) * n)。

需要注意的是，当括号对数较大时，暴力法的时间复杂度和空间复杂度非常高，因此在实际应用中，可以考虑使用动态规划或其他优化方法来解决。

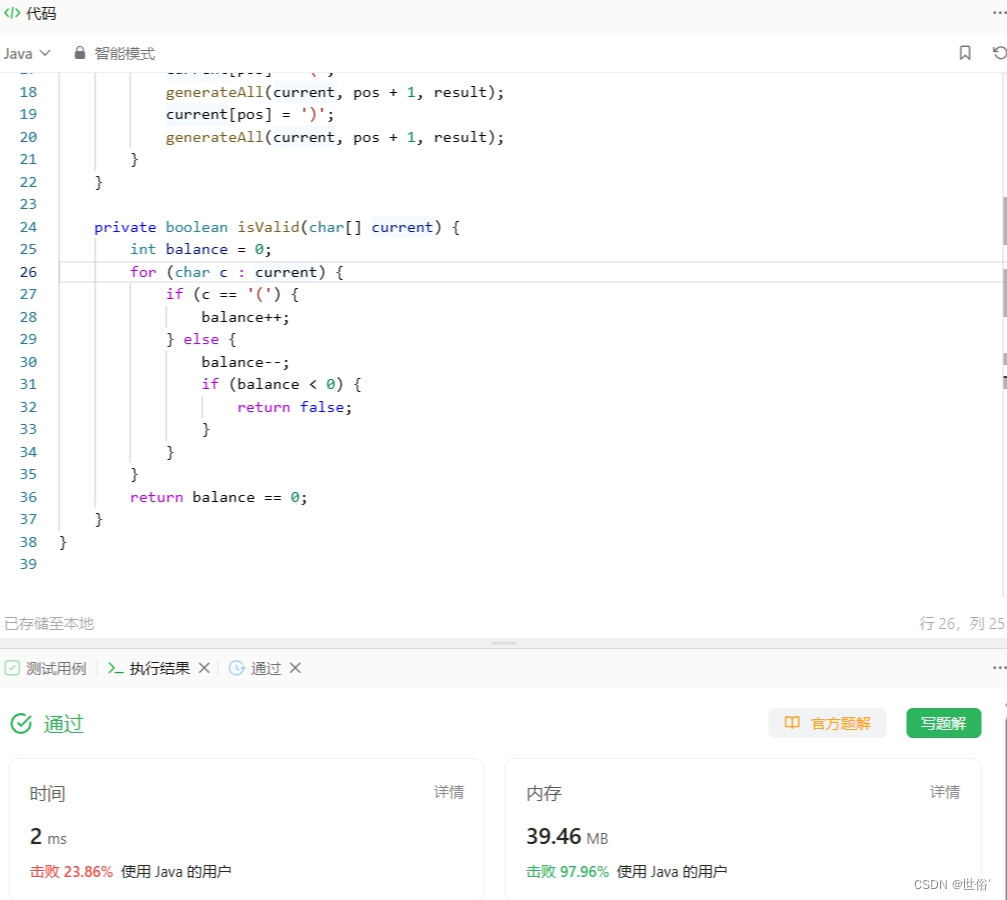
LeetCode运行结果：