dp训练题解

news2024/11/20 6:15:06

训练链接

CF101E

题目链接

点击打开链接

题目解法

朴素的 d p dp dp 很好写，但发现难以得到最优路径
考虑对于 ( x , y ) (x,y) (x,y) 的转移方式只有两种，可以想到用 b i t s e t bitset bitset 来维护转移，这样可以很节约空间
但我们发现开 n ∗ n n*n n∗n 的 b i t s e t bitset bitset 是不够的，可以考虑用时间来代替空间
于是可以只对后一半位置记录 b i t s e t bitset bitset，然后再做一次 d p dp dp，且记录前一半的 b i t s e t bitset bitset 转移
这样可以把空间优化掉一半，就可以过了
时间复杂度 O ( n m ) O(nm) O(nm)

#include <bits/stdc++.h>
using namespace std;
const int N=21000;
int n,m,p,f[2][N],x[N],y[N];
bitset<N/2> bs[N];
vector<int> ans;
inline int read(){
	int FF=0,RR=1;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;
	for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;
	return FF*RR;
}
void chkmax(int &x,int y){ x=max(x,y);}
int main(){
	n=read(),m=read(),p=read();
    for(int i=0;i<n;i++) x[i]=read();
    for(int i=0;i<m;i++) y[i]=read();
    for(int i=0;i<n;i++) bs[i].reset();
    f[0][0]=(x[0]+y[0])%p;
    for(int i=1;i<m;i++) f[0][i]=f[0][i-1]+(x[0]+y[i])%p;
	for(int i=1;i<n;i++){
        memset(f[i&1],0,sizeof(f[i&1]));
        f[i&1][0]=f[~i&1][0]+(x[i]+y[0])%p;bs[i][0]=1;
		for(int j=1;j<m;j++){
			chkmax(f[i&1][j],f[~i&1][j]+(x[i]+y[j])%p);
			chkmax(f[i&1][j],f[i&1][j-1]+(x[i]+y[j])%p);
            if(j>=m/2){
                if(f[~i&1][j]+(x[i]+y[j])%p>f[i&1][j-1]+(x[i]+y[j])%p) bs[i][j-m/2]=1;
                else bs[i][j-m/2]=0;
            }
		}
    }
	printf("%d\n",f[~n&1][m-1]);
    int pos=m-1,cur=n-1;
    for(;cur||pos;){
        if(bs[cur][pos-m/2]) cur--,ans.push_back(1);
        else pos--,ans.push_back(0);
        if(pos<m/2) break;
    }
    for(int i=0;i<n;i++) bs[i].reset();
    memset(f[0],0,sizeof(f[0]));
    f[0][0]=(x[0]+y[0])%p;
    for(int i=1;i<m;i++) f[0][i]=f[0][i-1]+(x[0]+y[i])%p;
    for(int i=1;i<=cur;i++){
        memset(f[i&1],0,sizeof(f[i&1]));
        f[i&1][0]=f[~i&1][0]+(x[i]+y[0])%p;bs[i][0]=1;
		for(int j=1;j<m/2;j++){
			chkmax(f[i&1][j],f[~i&1][j]+(x[i]+y[j])%p);
			chkmax(f[i&1][j],f[i&1][j-1]+(x[i]+y[j])%p);
            if(f[~i&1][j]+(x[i]+y[j])%p>f[i&1][j-1]+(x[i]+y[j])%p) bs[i][j]=1;
            else bs[i][j]=0;
		}
    }
    for(;cur||pos;){
        if(bs[cur][pos]) cur--,ans.push_back(1);
        else pos--,ans.push_back(0);
    }
    for(int i=ans.size()-1;i>=0;i--)
        if(ans[i]) putchar('C');
        else putchar('S');
	return 0;
}

CF67C

题目链接

点击打开链接

题目解法

如果只有前三个操作就很 simple
考虑最后一个操作交换
每次显然只会交换最近的两组可以交换的
于是时间复杂度 O ( n 2 ) O(n^2) O(n2)，感觉挺好理解的

#include <bits/stdc++.h>
#define lowbit(x) x&-x
using namespace std;
const int N=4100;
int n,m,ti,td,tr,te;
int dp[N][N];
char s[N],t[N];
int p1[N][26],p2[N][26];
inline int read(){
	int FF=0,RR=1;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;
	for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;
	return FF*RR;
}
void chkmin(int &x,int y){ x=min(x,y);}
int main(){
	ti=read(),td=read(),tr=read(),te=read();
	scanf("%s",s+1),scanf("%s",t+1);
	n=strlen(s+1),m=strlen(t+1);
	memset(dp,0x3f,sizeof(dp));
	dp[0][0]=0;
    for(int i=1;i<=n;i++){
        for(int j=0;j<26;j++) p1[i][j]=p1[i-1][j];
        p1[i][s[i]-'a']=i;
    }
    for(int i=1;i<=m;i++){
        for(int j=0;j<26;j++) p2[i][j]=p2[i-1][j];
        p2[i][t[i]-'a']=i;
    }
	for(int i=0;i<=n;i++){
		for(int j=0;j<=m;j++){
			if(!i&&!j) continue;
			if(i>0&&j>0&&s[i]==t[j]) chkmin(dp[i][j],dp[i-1][j-1]);
            if(i>1&&j>1){
                if(p2[j-1][s[i]-'a']&&p1[i-1][t[j]-'a']){
                    int k=p2[j-1][s[i]-'a'],l=p1[i-1][t[j]-'a'];
                    chkmin(dp[i][j],dp[l-1][k-1]+te+ti*(j-1-k)+td*(i-1-l));
                }
            }
			//insert
			if(j>0) chkmin(dp[i][j],dp[i][j-1]+ti);
			//delete
			if(i>0) chkmin(dp[i][j],dp[i-1][j]+td);
			//update
			if(i>0&&j>0) chkmin(dp[i][j],dp[i-1][j-1]+tr);
		}
    }
	printf("%d\n",dp[n][m]);
	fprintf(stderr, "%d ms\n", int(1e3 * clock() / CLOCKS_PER_SEC));
	return 0;
}

CF48G

题目链接

点击打开链接

题目解法

巨大恶心题！！！
简要题意：给定一个 n n n 点无向基环树，求每个点到其余点最短路之和
这道题一眼就会了，但代码是真的麻烦
基环树无非破环为链，然后先考虑子树内的距离和，然后再考虑环上其他子树的贡献
这里需要讨论的地方就是两点只会走 ≤ 1 2 \le \frac{1}{2} ≤21​环长的链，这个有一些细节需要考虑
一个比较轻松的写法是倍长环
时间复杂度 O ( n ) O(n) O(n)

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=400100;
int n,ans[N];
bool flg;
int e[N<<1],ne[N<<1],w[N<<1],h[N],idx;
int stk[N],top;
int cir[N],cnt,cw[N];
bool oncir[N],vis[N];
int totd[N],siz[N];
inline int read(){
	int FF=0,RR=1;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;
	for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;
	return FF*RR;
}
bool find_cir(int u,int from){
	stk[++top]=u,vis[u]=1;
	for(int i=h[u];~i;i=ne[i]){
		int v=e[i];
		if(v==from) continue;
        if(flg) return true;
		if(vis[v]){//find a circle
			while(top&&stk[top]!=v) oncir[stk[top]]=1,cir[++cnt]=stk[top--];
            oncir[v]=1,cir[++cnt]=v;
            flg=1;
			return true;
		}
		if(find_cir(v,u)) return true;
	}
	vis[u]=0,top--;
	return false;
}
void dfs1(int u,int fa){
	totd[u]=0,siz[u]=1;
	for(int i=h[u];~i;i=ne[i])
		if(e[i]!=fa&&!oncir[e[i]]){
            dfs1(e[i],u);
			totd[u]+=totd[e[i]]+siz[e[i]]*w[i];
			siz[u]+=siz[e[i]];
		}
}
void dfs2(int u,int fa,int updis,int rt){
    int tmp=totd[u];
	totd[u]+=updis;
	for(int i=h[u];~i;i=ne[i]){
		int v=e[i];
		if(v!=fa&&!oncir[e[i]])
            dfs2(v,u,updis+tmp-totd[v]-siz[v]*w[i]+(siz[rt]-siz[v])*w[i],rt);
	}
}
void dfs3(int u,int fa,int v1,int v2,int curd){
	ans[u]+=v1+v2*curd;
	for(int i=h[u];~i;i=ne[i]) if(e[i]!=fa&&!oncir[e[i]]) dfs3(e[i],u,v1,v2,curd+w[i]);
}
void add(int x,int y,int z){ e[idx]=y,w[idx]=z,ne[idx]=h[x],h[x]=idx++;}
signed main(){
	n=read();
    memset(h,-1,sizeof(h));
	for(int i=1;i<=n;i++){
		int a=read(),b=read(),c=read();
		add(a,b,c),add(b,a,c);
	}
	for(int i=1;i<=n;i++) if(!vis[i]) find_cir(i,-1);
	for(int i=1;i<=cnt;i++) dfs1(cir[i],-1),dfs2(cir[i],-1,0,cir[i]);
	for(int i=1;i<=n;i++) ans[i]=totd[i];
	for(int i=1;i<=cnt;i++) cir[i+cnt]=cir[i];
    for(int i=2;i<=cnt+1;i++){
        int ww=0;
        for(int j=h[cir[i]];~j;j=ne[j]) if(e[j]==cir[i-1]) ww=w[j];
        cw[i]=cw[i+cnt]=ww;
    }
    for(int i=1;i<=cnt<<1;i++) cw[i]+=cw[i-1];
    int totlenth=cw[cnt+1];
	int tot=0,totsiz=0;
	for(int i=1,j=1;i<=cnt<<1;i++){
        while((cw[i]-cw[j])*2>totlenth){
            tot-=totd[cir[j]]-siz[cir[j]]*cw[j],totsiz-=siz[cir[j]];
            j++;
        }
        if(i>cnt){
			int res=totsiz*cw[i]+tot;
			dfs3(cir[i],-1,res,totsiz,0);
		}
		tot+=totd[cir[i]]-siz[cir[i]]*cw[i],totsiz+=siz[cir[i]];
	}
    tot=0,totsiz=0;
	for(int i=cnt<<1,j=cnt<<1;i;i--){
        while((cw[j]-cw[i])*2>=totlenth){
            tot-=totd[cir[j]]+siz[cir[j]]*cw[j],totsiz-=siz[cir[j]];
            j--;
        }
		if(i<=cnt){
			int res=-totsiz*cw[i]+tot;
			dfs3(cir[i],-1,res,totsiz,0);
		}
		tot+=totd[cir[i]]+siz[cir[i]]*cw[i],totsiz+=siz[cir[i]];
	}
	for(int i=1;i<=n;i++) printf("%lld ",ans[i]);puts("");
	fprintf(stderr,"%d ms\n",int64_t(1e3*clock()/CLOCKS_PER_SEC));
	return 0;
}

CF11E

看到百分比，需要想到 01 01 01 分数规划，这是一个很重要的思路
然后直接套路二分 +    d p + \;dp +dp 既可
即每正确一步就会 + 1 +1 +1，每走一步就会 − m i d -mid −mid
不难直接 d p dp dp
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)

#include <bits/stdc++.h>
using namespace std;
const int N=2000100;
const double eps=1e-9,inf=1000000000;
char str[N],t[N];
int n;
double dp[N][2];
inline int read(){
	int FF=0,RR=1;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;
	for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;
	return FF*RR;
}
inline double max(double x,double y){
	if(x>y)return x;
	return y;
}
bool check(double mid){//每选一个数就会-mid
	dp[0][1]=0,dp[0][0]=-mid;
	for(int i=1;i<=n;i++){
		dp[i][0]=max(dp[i-1][0]+(str[i]=='R')-2.0*mid,dp[i-1][1]+(str[i]=='L')-mid);
		dp[i][1]=max(dp[i-1][1]+(str[i]=='L')-2.0*mid,dp[i-1][0]+(str[i]=='R')-mid);
	}
	return dp[n][1]>=0;
}
int main(){
	scanf("%s",str+1);
	n=strlen(str+1);
    int len=0;
    if(str[1]==str[n]&&str[1]=='R') t[++len]='X';
    t[++len]=str[1];
    for(int i=2;i<=n;i++){
        if(str[i]==str[i-1]&&str[i]!='X') t[++len]='X';
        t[++len]=str[i];
    }
    if(str[1]==str[n]&&str[1]=='L') t[++len]='X';
    n=len;
    for(int i=1;i<=len;i++) str[i]=t[i];
	double l=0,r=100+eps;
	while(l<r-eps){
		double mid=(l+r)/2;
		check(mid/100)?l=mid:r=mid;
	}
	printf("%.6lf\n",(int)(r*1000000)/1000000.0);
	fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));
	return 0;
}

CF321D

题目链接

点击打开链接

题目解法

有些妙的题！
考虑一个结论：一个网格可以通过任意次操作得到，当且仅当 a i , x ⊕ a i , m ⊕ a i , x + m = 0    ( 1 ≤ x < m ) a_{i,x}\oplus a_{i,m}\oplus a_{i,x+m}=0\;(1\le x< m) ai,x​⊕ai,m​⊕ai,x+m​=0(1≤x<m)，对于 a y , j a_{y,j} ay,j​ 也同理
这个结论感性理解是好理解的，必要性是如果翻了 a i , x a_{i,x} ai,x​ 或 a i , x + m a_{i,x+m} ai,x+m​ 那么一定会翻到 a i , m a_{i,m} ai,m​，那么异或和始终唯一，充分性我只会感性理解，可能可以通过构造的方式得出
这样就只需要枚举 m ∗ m m*m m∗m 的网格状态，就可以确定其他网格的状态
我们发现第 m m m 行是一个关键行，因为上下异或都需要用到它，所以考虑状压这一行前 m m m 列的状态
然后一行一行往下计算，因为这时在每个区域（可以以 ( m , m ) (m,m) (m,m) 把网格分成 4 个区域）的状态互不影响，所以可以通过一些判断计算出来，这个不难计算
时间复杂度 O ( 2 m m 2 ) O(2^mm^2) O(2mm2)
感觉一开始的小结论有些妙，其他比较套路

#include <bits/stdc++.h>
using namespace std;
const int N=40;
int a[N][N];
inline int read(){
	int FF=0,RR=1;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;
	for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;
	return FF*RR;
}
int calc(int x,int y){
	if(y) return -x;
	return x;
}
void chkmax(int &x,int y){ x=max(x,y);}
int main(){
	int n=read(),m=(n+1)/2;
	for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) a[i][j]=read();
    int ans=-1e9;
	for(int S=0;S<1<<m;S++){//枚举第m行前m个的状态
		int Sm=S>>(m-1)&1;
		int res=calc(a[m][m],Sm);
		for(int i=0;i<m-1;i++){
			int p=S>>i&1,q=Sm^p;
			res+=calc(a[m][i+1],p)+calc(a[m][i+m+1],q);
		}
		for(int j=1;j<m;j++){//枚举第j行
			int MX=-1e9;
			for(int Sj=0;Sj<2;Sj++){
				int rs=calc(a[j][m],Sj)+calc(a[j+m][m],Sj^Sm);
				for(int k=1;k<m;k++){
					int mx=-1e9;
					for(int A=0;A<2;A++){//(x,y)
						int B=A^Sj;//(x,y+m)
						int C=A^(S>>(k-1)&1);//(x+m,y)
						int D=C^(Sm^Sj);//(x+m,y+m)
						chkmax(mx,calc(a[j][k],A)+calc(a[j][k+m],B)+calc(a[j+m][k],C)+calc(a[j+m][k+m],D));
					}
					rs+=mx;
				}
				chkmax(MX,rs);
			}
			res+=MX;
		}
		ans=max(ans,res);
	}
	printf("%d\n",ans);
	fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));
	return 0;
}

CF251E

题目链接

点击打开链接

题目解法

很好的题！！！
参考了 Luogu 的题解，感觉很妙
显然存在度数大于 4 4 4 的点答案就是 0 0 0，直接特判掉
我们任意找一个三度点作为根，这一步主要是为了把问题分成左右两边去分治
这里需要特判掉一条链的情况
考虑令 d p u dp_u dpu​ 表示用 i i i 的子树填满一个 2 × s i z u 2 2\times \frac{siz_u}{2} 2×2sizu​​ 的方格的方案数
我们找到在 u u u 的子树内离 u u u 最近的二度点
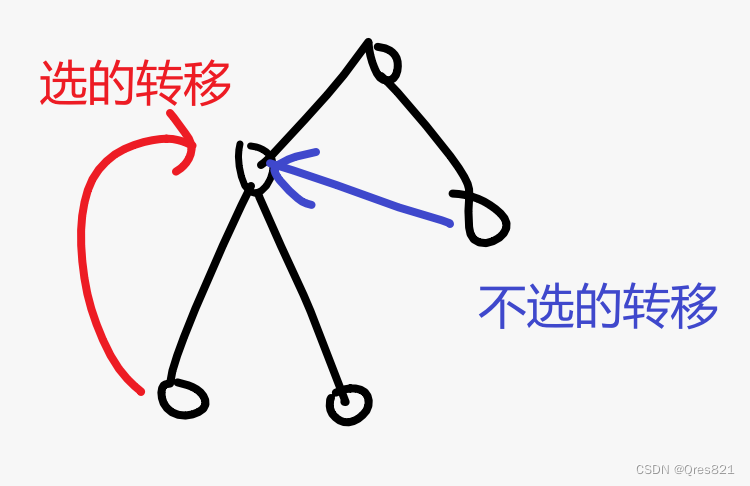
发现可能的情况有：
在这里插入图片描述
其中 y y y 可能是在上面也可能是在下面，这都是小事
所以我们可以枚举 v v v 的那个儿子处在下面，那个继续往左边延伸
然后就是复杂的分类讨论（令 v v v 的两个儿子分别为 w 1 , w 2 w1,w2 w1,w2，不妨令 v v v 在下面，且 w 1 w1 w1 为第一步向上延伸的， w 2 w2 w2 为第一步向左延伸的）
这里需要引入一个新的 d p dp dp 数组 g x , y g_{x,y} gx,y​ 表示把 x x x 的子树和 y y y 的子树分别往同一个方向延伸的方案数

  1. w 2 w2 w2 和 w 1 w1 w1 的儿子一起往右延伸，即为 g w 2 , s o n w 1 g_{w2,son_{w1}} gw2,sonw1​​，条件是 w 1 w1 w1 只有一个儿子
  2. w 1 w1 w1 的子树是链，且可以往右边延伸，那么 w 2 w2 w2 就独占 2 × s i z w 2 2 2\times \frac{siz_{w2}}{2} 2×2sizw2​​ 的网格
  3. w 1 w1 w1 为有 2 个儿子，那么需要考虑哪一个儿子与 w 1 w1 w1 一起往左延伸，哪一个儿子往右延伸

有亿些情况需要特判，因为 d p dp dp 和 g g g 需要互相调用，所以这里使用记忆化搜索，时间复杂度 O ( n ) O(n) O(n)

#include <bits/stdc++.h>
using namespace std;
const int N=200100,P=1e9+7;
int n,dp[N];
int deg[N],nxt2[N],dwlen[N],siz[N];
int e[N<<1],ne[N<<1],h[N],idx;
vector<int> G[N];
inline int read(){
	int FF=0,RR=1;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;
	for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;
	return FF*RR;
}
void add(int x,int y){ e[idx]=y,ne[idx]=h[x],h[x]=idx++;}
void dfs(int u,int fa){
    siz[u]=1;
	for(int i=h[u];~i;i=ne[i]){
		int v=e[i];
		if(v==fa) continue;
		G[u].push_back(v),dfs(v,u);
		siz[u]+=siz[v];
		nxt2[u]=nxt2[v],dwlen[u]=dwlen[v]+1;
	}
	if(G[u].size()==2) nxt2[u]=u,dwlen[u]=0;
}
inline void inc(int &x,int y){
	x+=y;
	if(x>=P) x-=P;
}
int calc1(int u);
int calc2(int u1,int u2){
	if((siz[u1]+siz[u2])&1) return 0;
	if(!u1||!u2) return calc1(u1|u2);
	if(G[u1].size()>1||G[u2].size()>1) return 0;
    if(!G[u1].size()&&!G[u2].size()) return 1;
	if(!G[u1].size()) return calc1(G[u2][0]);
	if(!G[u2].size()) return calc1(G[u1][0]);
	return calc2(G[u1][0],G[u2][0]);
}
int calc1(int u){
	if(!u) return 1;
	if(siz[u]&1) return 0;
	if(dp[u]!=-1) return dp[u];
	if(!nxt2[u]) return siz[u]/2;
	int v1=G[nxt2[u]][0],v2=G[nxt2[u]][1],res=0;
	for(int k=0;k<2;k++){
		if(G[v1].size()==1) inc(res,calc2(v2,G[v1][0]));
        if(!nxt2[v1]&&dwlen[v1]<=dwlen[u]) inc(res,calc1(v2)*((dwlen[v1]!=dwlen[u])+1)%P);
		if(G[v1].size()==2){
			int w1=G[v1][0],w2=G[v1][1];
			if(!nxt2[w1]&&dwlen[w1]<dwlen[u]) inc(res,calc2(w2,v2));
            if(!nxt2[w2]&&dwlen[w2]<dwlen[u]) inc(res,calc2(w1,v2));
		}
		swap(v1,v2);
	}
	return dp[u]=res;
}
int main(){
	n=read();n<<=1;
    memset(h,-1,sizeof(h));
	for(int i=1;i<n;i++){
		int x=read(),y=read();
		add(x,y),add(y,x),deg[x]++,deg[y]++;
	}
	for(int i=1;i<=n;i++) if(deg[i]>3){ puts("0");exit(0);}
	int mxdeg=0;
	for(int i=1;i<=n;i++) mxdeg=max(mxdeg,deg[i]);
    if(mxdeg==1){ puts("2");exit(0);}
	if(mxdeg==2){ printf("%d",1ll*2*(n+1ll*(n/2-1)*(n/2-2)%P)%P);exit(0);}
	int rt,ans=0;
	for(int i=1;i<=n;i++) if(deg[i]==3) rt=i;
	memset(dp,-1,sizeof(dp));
	dfs(rt,0);
    for(int i=1;i<=n;i++) sort(G[i].begin(),G[i].end());
	do{
		int u=G[rt][0],v=G[rt][1],w=G[rt][2];
        if(G[u].size()>2) continue;
		if(!G[u].size()) inc(ans,1ll*calc1(v)*calc1(w)%P);
		if(G[u].size()==1) inc(ans,1ll*calc1(v)*calc2(w,G[u][0])%P),inc(ans,1ll*calc1(w)*calc2(v,G[u][0])%P);
		if(G[u].size()==2) inc(ans,1ll*calc2(v,G[u][0])*calc2(w,G[u][1])%P),inc(ans,1ll*calc2(v,G[u][1])*calc2(w,G[u][0])%P);
	}while(next_permutation(G[rt].begin(),G[rt].end()));
	printf("%d\n",2*ans%P);
	fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1035422.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

113双周赛

113双周赛

题目列表 2855. 使数组成为递增数组的最少右移次数 2856. 删除数对后的最小数组长度 2857. 统计距离为 k 的点对 2858. 可以到达每一个节点的最少边反转次数 一、使数组成为递增数组的最少右移次数 这题可以直接暴力求解&#xff0c;枚举出每种右移后的数组&#xff0c;将…
阅读更多...
MySQL学习笔记4

MySQL学习笔记4

客户端工具的使用&#xff1a; MySQL&#xff1a; mysql命令行工具&#xff0c;一般用来连接访问mysql的数据。 案例&#xff1a;使用mysql客户端工具连接服务器端&#xff08;用户名&#xff1a;root&#xff1b;密码&#xff1a;123456&#xff09;. [rootmysql-server ~]#…
阅读更多...
不甘于被强势厂商捆绑，中国移动未来或自研5G基站

不甘于被强势厂商捆绑，中国移动未来或自研5G基站

一直以来运营商被认为只是做服务&#xff0c;而设备等都是由设备商提供的&#xff0c;甚至由于如今的设备高度复杂&#xff0c;设备商已承包越来越多的基站运维工作&#xff0c;运营商的技术水平越来越低&#xff0c;不过随着中国移动发布5G射频芯片8676&#xff0c;似乎显示出…
阅读更多...
Latex字体大小

Latex字体大小

阅读更多...
centos7用docker安装WireGuard教程

centos7用docker安装WireGuard教程

1、 检查centos内核版本 uname -r2、升级内核 下载脚本上传到服务器运行脚本进行升级内核 链接&#xff1a;https://pan.baidu.com/s/1vYmqVy2St3nFnJWGPIwdOw 提取码&#xff1a;owac 3、安装WireGuard 方案一&#xff1a;使用脚本安装 执行第二步脚本进行安装#启动wg0wg…
阅读更多...
CSRF攻击（跨站请求伪造）

CSRF攻击（跨站请求伪造）

1.CSRF原理 程序员开发的时候&#xff0c;未对相关页面进行token和referer判断&#xff0c;造成攻击者可构造自己的URL地址欺骗用户进行点击 漏洞分析&#xff08;低级可绕过&#xff09; 通过这个可以更改密码 改为了password 中级多了referer头可以绕过 源代码 多了一个refer…
阅读更多...
简单好用的Python装饰器详解

简单好用的Python装饰器详解

装饰器&#xff08;Decorators&#xff09;是Python中一种强大而灵活的功能&#xff0c;用于修改或增强函数或类的行为。装饰器本质上是一个函数&#xff0c;它接受另一个函数或类作为参数&#xff0c;并返回一个新的函数或类。它们通常用于在不修改原始代码的情况下添加额外的…
阅读更多...
linux服务器加固-密码验证设置

linux服务器加固-密码验证设置

安全问题 安全控制点 风险分析 风险等级 标准要求 查看登录/etc/login.defs文件PASS_MAX_DAYS参数为99999&#xff0c;查看/etc/pam.d/system-auth文件&#xff0c;未对密码策略进行有效配置&#xff0c;如&#xff1a;密码更换周期&#xff0c;密码是否包括字母、数字与特…
阅读更多...
基于SpringBoot的网上点餐系统

基于SpringBoot的网上点餐系统

目录 前言 一、技术栈 二、系统功能介绍 用户功能模块 管理员功能模块 美食店功能模块 前台首页功能模块 三、核心代码 1、登录模块 2、文件上传模块 3、代码封装 前言 系统管理也都将通过计算机进行整体智能化操作&#xff0c;对于网上点餐系统所牵扯的管理及数据保存…
阅读更多...
【从0学习Solidity】 32. 代币水龙头

【从0学习Solidity】 32. 代币水龙头

【从0学习Solidity】32. 代币水龙头 博主简介&#xff1a;不写代码没饭吃&#xff0c;一名全栈领域的创作者&#xff0c;专注于研究互联网产品的解决方案和技术。熟悉云原生、微服务架构&#xff0c;分享一些项目实战经验以及前沿技术的见解。关注我们的主页&#xff0c;探索全…
阅读更多...
兴达易控EtherCAT转Modbus网关用Modbus Slave模拟从站配置案例

兴达易控EtherCAT转Modbus网关用Modbus Slave模拟从站配置案例

兴达易控EtherCAT到Modbus网关可以用作Modbus从站的配置。EtherCAT到Modbus网关允许Modbus协议转换为EtherCAT&#xff0c;实现不同通信系统之间的互操作性。通过配置从站到网关的Modbus&#xff0c;您可以访问和控制Modbus设备。同时&#xff0c;网关还可以扩展Modbus网络的范…
阅读更多...
[C++基础]-继承

[C++基础]-继承

前言 作者&#xff1a;小蜗牛向前冲 名言&#xff1a;我可以接受失败&#xff0c;但我不能接受放弃 如果觉的博主的文章还不错的话&#xff0c;还请点赞&#xff0c;收藏&#xff0c;关注&#x1f440;支持博主。如果发现有问题的地方欢迎❀大家在评论区指正。 目录 一、模板的…
阅读更多...
2023-9-23 最大不相交区间数量

2023-9-23 最大不相交区间数量

题目链接&#xff1a;最大不相交区间数量 #include <iostream> #include <algorithm>using namespace std;const int N 100010;int n;struct Range {int l, r;bool operator< (const Range &W) const {return r < W.r;} }range[N];int main() {cin >…
阅读更多...
Unity中的两种ScriptingBackend

Unity中的两种ScriptingBackend

一&#xff1a;前言 二&#xff1a;两种模式的介绍 ios&#xff1a;unity只有il2cpp模式的编译才支持64位系统&#xff0c;mono是不支持的&#xff0c;在快速开发阶段仍然支持Mono&#xff0c;但是不能再向Apple提交Mono(32位)的应用 苹果在2016年1月就要求所有新上架游戏必须支…
阅读更多...
ASO优化之竞争对手的选择取决于什么

ASO优化之竞争对手的选择取决于什么

任何具有良好ASO策略的应用程序都是来自于良好的基准&#xff0c;不仅可以对市场有总体概述&#xff0c;还可以发现应用的增长潜力以及如何在不同的应用商店中获得知名度。在发布应用之前&#xff0c;需要制定ASO策略以获得搜索和浏览可见性&#xff0c;所以研究竞争对手是基础…
阅读更多...
【小沐学NLP】关联规则分析Apriori算法（Mlxtend库，Python）

【小沐学NLP】关联规则分析Apriori算法（Mlxtend库，Python）

文章目录 1、简介2、Mlxtend库2.1 安装2.2 功能2.2.1 User Guide2.2.2 User Guide - data2.2.3 User Guide - frequent_patterns 2.3 入门示例 3、Apriori算法3.1 基本概念3.2 apriori3.2.1 示例 1 -- 生成频繁项集3.2.2 示例 2 -- 选择和筛选结果3.2.3 示例 3 -- 使用稀疏表示…
阅读更多...
Klocwork 2023.2 windows

Klocwork 2023.2 windows

Klocwork 2023.2 windows 2692407267qq.com&#xff0c;更多内容请见http://user.qzone.qq.com/2692407267/
阅读更多...
es6新语法特性+vue2的学习笔记

es6新语法特性+vue2的学习笔记

1. es6 ECMA的第6版&#xff0c;15年发布&#xff0c;规定新的语法特性 2. let声明变量 varlet声明的变量会越狱声明的变量有严格的作用域可以声明多次只能声明一次会变量提升(未声明的变量不会报错)不会变量提升 代码案例&#xff1a; <script>// {// var a 1;/…
阅读更多...
点分治维护dp+连通块上新型dp思路+乘积方面进行根号dp：0922T4

点分治维护dp+连通块上新型dp思路+乘积方面进行根号dp：0922T4

首先连通块&#xff0c;所以点分治肯定是 Trick1 钦定选根的连通块dp 对于钦定选根的连通块dp&#xff0c;有一种常见思路 先对原树求其dfn序&#xff0c;按dfn序倒序求解 具体的&#xff0c;对于当前点 i i i&#xff08;注意这里都是指dfn序&#xff09;&#xff0c;我们…
阅读更多...
如何申请办理400电话？

如何申请办理400电话？

导语&#xff1a;随着企业的发展和市场竞争的加剧&#xff0c;越来越多的企业开始意识到拥有一个400电话的重要性。本文将介绍如何申请办理400电话&#xff0c;帮助企业提升客户服务质量和品牌形象。 一、了解400电话的概念和优势 400电话是一种企业客服电话号码&#xff0c;…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023