题目列表

2855. 使数组成为递增数组的最少右移次数

2856. 删除数对后的最小数组长度

2857. 统计距离为 k 的点对

2858. 可以到达每一个节点的最少边反转次数

一、使数组成为递增数组的最少右移次数

这题可以直接暴力求解，枚举出每种右移后的数组，将它和排完序后的数组比较，时间复杂度为O(n^2)

代码如下

class Solution {
public:
    int minimumRightShifts(vector<int>& nums) {
        vector<int> v=nums;
        sort(v.begin(),v.end());
        for(int i=0;i<nums.size();i++){
            if(v==nums) return i;
            nums.insert(nums.begin(),nums.back());
            nums.pop_back();
        }
        return -1;
    }
};

这个能过，但是有没有更快的算法，我们观察一下这个数组，如果它要是能右移成递增数组，那么它必然是由两个递增数组构成的，且前一个数组的最小值，一定大于后一个数组的最大值，答案就是第二个数组的长度，所以我们只要试着将数组拆分成两个递增数组就行(边界条件挺多，一定要细节)，时间复杂度为O(n)

代码如下

class Solution {
public:
    int minimumRightShifts(vector<int>& nums) {
        int end1=0,n=nums.size();
        while(end1+1<n&&nums[end1]<nums[end1+1])
            end1++;
        if(end1==n-1) return 0;
        int end2=end1+1;
        while(end2+1<n&&nums[end2]<nums[end2+1])
            end2++;
        if(end2!=n-1||nums[0]<nums[n-1]) return -1;
        else return n-end1-1;
    }
};

二、删除数对后的最小数组长度

这题还是比较难想到的，比较绕。我们需要多枚举几个例子，然后就会发现，当某个数的个数cnt大于等于数组长度n的一半时，最优的方案就是将它前后的数都与它相互抵消(因为如果还让其他数相互抵消，那么剩余的和该数相抵消的元素个数就会变小，从而该元素剩下的个数就会变多)，所以答案就是cnt-(n-cnt)=2*cnt-n，那么如果没有一个数的个数大于数组长度的一半呢？

首先从最特殊的数组中数字都是唯一的情况开始讨论，那么显然，当数组长度为偶数时，答案为0，当数组长度为奇数时，答案为1，那么是不是所有的情况都符合这个规律呢？答案是，确实都符合这个规律，因为所有的数的个数都<n/2，那么我们就可以通过抵消，将数的个数全部化成1

代码如下

class Solution {
public:
    int minLengthAfterRemovals(vector<int>& nums) {
        unordered_map<int,int>cnt;
        int n=nums.size(),ans=n&1;//n&1，奇数为1，偶数为0
        for(auto x:nums)
            ++cnt[x];
        for(auto [x,y]:cnt)
            if(y>n/2)
                ans=max(ans,2*y-n);
        return ans;
    }
};

当然这题如果想不到这么深，那么也可以用最基本的贪心，每次拿出出现次数最大的两个元素相抵消，直到剩下零个数或剩下一个数为止。代码如下

class Solution {
public:
    int minLengthAfterRemovals(vector<int>& nums) {
        unordered_map<int,int>cnt;
        int n=nums.size(),ans=n&1;
        for(auto x:nums)
            ++cnt[x];
        priority_queue<int>q;
        for(auto [x,y]:cnt)
            q.push(y);
        while(q.size()>1){
            int x=q.top();q.pop();
            int y=q.top();q.pop();
            x--,y--;
            if(x)q.push(x);
            if(y)q.push(y);
        }
        return q.empty()?0:q.top();
    }
};

三、统计距离为k的点对

看到两个数的和k，以及k的数据范围，我们就要想到这题能用暴力枚举点来做，然后通过枚举到的点，求出与之相对应的点的坐标，答案加上之前出现的该点个数(用哈希表统计)，代码如下

class Solution {
public:
    int countPairs(vector<vector<int>>& coordinates, int k) {
        int n=coordinates.size();
        unordered_map<long long,int>cnt;
        int ans=0;
        for(auto& e:coordinates){
            int x=e[0],y=e[1];
            for(int i=0;i<=k;i++){
                auto it=cnt.find((x^i)*1000000LL+(y^(k-i)));
                if(it!=cnt.end())
                    ans+=it->second;
            }
            cnt[x*1000000LL+y]++;
        }
        return ans;
    }
};

 四、可以到达每一个节点的最小边反转次数

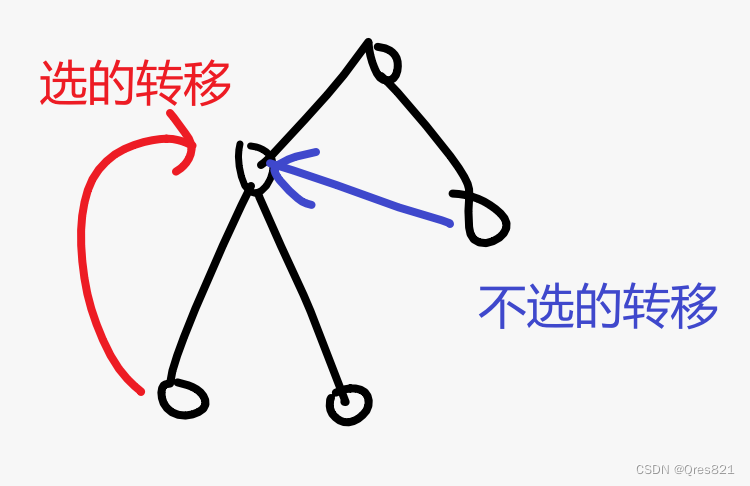
这题是换根dp，即通过根节点的最小边反转次数，来得到它孩子结点的最小边反转次数，因为它的孩子结点的反转边的个数就和它父节点的最小边反转次数相差一个它俩之间的边是否需要翻转，其它的都一样。

代码如下

class Solution {
public:
    vector<int> minEdgeReversals(int n, vector<vector<int>>& edges) {
        //建图
        vector<vector<pair<int,int>>>g(n);
        for(auto& e:edges){
            int x=e[0],y=e[1];
            g[x].push_back({y,1});//顺便记录一下边的方向，1为正，-1为逆
            g[y].push_back({x,-1});
        }

        vector<int>ans(n);
        //计算根节点的最少边反转次数
        function<void(int,int)>dfs=[&](int x,int fa){
            for(auto& [y,dir]:g[x]){
                if(y!=fa){
                    ans[0]+=(dir<0);//方向反的需要反转
                    dfs(y,x);
                }
            }
        };
        dfs(0,-1);

        //换根dp
        function<void(int,int)>reroot=[&](int x,int fa){
            for(auto& [y,dir]:g[x]){
                if(y!=fa){
                    ans[y]=ans[x]+dir;
                    reroot(y,x);
                }
            }
        };
        reroot(0,-1);
        return ans;
    }
};