课程地址和说明

自动求导实现p2
本系列文章是我学习李沐老师深度学习系列课程的学习笔记，可能会对李沐老师上课没讲到的进行补充。

自动求导

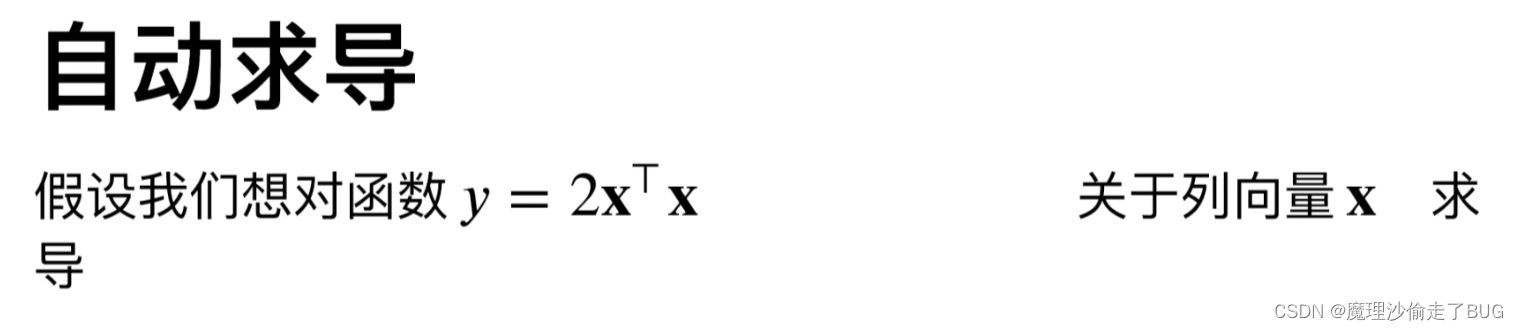
# 创建变量
import torch
x = torch.arange(4, dtype=torch.float32) #只有浮点数才能求导
# 计算y关于x的梯度之前，需要一个地方存储梯度
x.requires_grad_(True)
print("x为：",x)
# 计算y
y = 2 * torch.dot(x,x) # y=2倍的x向量的内积，即y=2x^2
print("y为：",y)
# 通过调用反向传播函数来自动计算y关于x每个分量的梯度
y.backward() # 求导,y'=4x
print("x的梯度为：",x.grad)
print("y的导数是否为y'=4x：",x.grad == 4 * x)

运行结果：

x为： tensor([0., 1., 2., 3.], requires_grad=True)
y为： tensor(28., grad_fn=<MulBackward0>)
x的梯度为： tensor([ 0., 4., 8., 12.])
y的导数是否为y’=4x： tensor([True, True, True, True])

默认情况下PyTorch会把梯度累积起来

所以我们在算下一步的时候需要讲梯度清零

• 举一个例子，之前的章节说过，当$y=sum(\overrightarrow{x})=\sum _{i=1}^m{x}_i=x_1+x_2+\cdots +x_m$，$a$为任意常数，$u=g(\overrightarrow{x})$时，有：
  $$\frac{\partial y}{\partial \overrightarrow{x}}={\left[\begin{array}{c}\frac{\partial f(\overrightarrow{x})}{\partial x_1}\\ \frac{\partial f(\overrightarrow{x})}{\partial x_2}\\ ⋮\\ \frac{\partial f(\overrightarrow{x})}{\partial x_m}\end{array}\right]}_{m\times 1}={\left[\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right]}_{m\times 1}$$最终结果是单位向量。
  用PyTorch复现为：

# 在默认情况下，PyTorch会累积梯度，我们需要清除之前的值
x.grad.zero_()
# 重新定义，y=x1+x2+...+xn
y = sum(x)
# 向后传播求导
y.backward()
# 打印求导结果
print(x.grad)

运行结果：
tensor([1., 1., 1., 1.])

深度学习中，我们的目的不是计算微分矩阵，而是批量中每个样本单独计算的偏导数之和。

# 在默认情况下，PyTorch会累积梯度，我们需要清除之前的值
x.grad.zero_()
# 重新定义，y=x1+x2+...+xn
y = x * x # 变为了标量
print("y=",y)
# 向后传播求导
y.sum().backward() # 变量需要先让y求和再向后传播求导
print("y.sum()=",y.sum())
# 打印求导结果
print(x.grad)

运行结果：
y= tensor([0., 1., 4., 9.], grad_fn=<MulBackward0>)
y.sum()= tensor(14., grad_fn=<SumBackward0>)
tensor([0., 2., 4., 6.])

将某些计算移动到记录的计算图之外

# 清空累积的梯度
x.grad.zero_()
# 定义y = x * x
y = x* x
# 定义u为常数，不再是y = x * x这样的函数，其常数值为x * x
u = y.detach()
print(u)
# z = u * x，相当于常数u乘以向量x
z = u * x
# z = [u1,u2,u3,u4]（常数向量）×[x1,x2,x3,x4]^T（变量向量）
# z = u1x1+u2x2+u3x3+u4x4
# 所以z'x1=u1，以此类推，其偏导数的向量最终就和u相等
z.sum().backward()
print(x.grad  == u)

运行结果：
tensor([0., 1., 4., 9.])
tensor([True, True, True, True])

# 清空累积的梯度
x.grad.zero_()
# 现在y为 x^2(x1^2+x2^2+x3^2+x4^2)，y'=2x(y'x1=2x1，以此类推)
# 对y求导
y.sum().backward()
# 证明y的导数是否是2x
print(x.grad ==2 *x)

运行结果：
tensor([True, True, True, True])

【提问】请用通俗的语言告诉我在PyTorch中， y.sum().backward()与y.backward()这两种向后求导方式有什么区别？
【chatGPT回答】在PyTorch中，y.sum().backward()和y.backward()是两种不同的向后求导方式，它们在计算梯度的方式上有一些区别。

1. y.sum().backward()

• 这个方式首先对y进行了求和操作，将一个张量中的所有元素相加得到一个标量（一个单一的数值）。
• 然后对这个标量进行反向传播，计算相对于y的梯度。
• 这种方式通常用于处理损失函数的梯度计算，因为损失函数通常返回一个标量，你希望计算相对于模型参数的梯度。

2. y.backward()：

• 这个方式直接对张量y进行反向传播，计算相对于y的梯度。
• 这种方式通常用于计算中间变量的梯度，而不是损失函数的梯度。
  总的来说，主要区别在于：
• y.sum().backward()用于计算损失函数相对于模型参数的梯度，因为损失函数通常返回一个标量值。
• y.backward()用于计算中间变量相对于其他变量的梯度，通常在计算模型的中间层时使用。
  选择哪种方式取决于你的具体需求和计算图的结构。通常，当你需要计算损失函数相对于模型参数的梯度时，你会使用y.sum().backward()，而在其他情况下，你会使用y.backward()来计算相对于中间变量的梯度。

即使构建函数的计算图需要通过Python控制流（例如，条件循环或任意函数调用)，我们仍然可以计算得到的变量的梯度

# 清空累积的梯度
x.grad.zero_()
# 设定一个函数
def f(a):
    b = a * 2
    # 如果b向量的模长（L2范式）小于1000，就不断给它乘以2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c
# 取一个随机数标量作为其值
a = torch.randn(size=(),requires_grad=True)
print("a为：",a)
d = f(a)
print("f(a)为：",d)
d.backward()
# 此函数相当于f(a)=ba，b是系数，如果是向量也是如此
# 所以其导数（或向量对应梯度向量）一定是斜率b
print(a.grad == d/a)

运行结果：
a为： tensor(1.6346, requires_grad=True)
f(a)为： tensor(1673.8451, grad_fn=)
tensor(True)