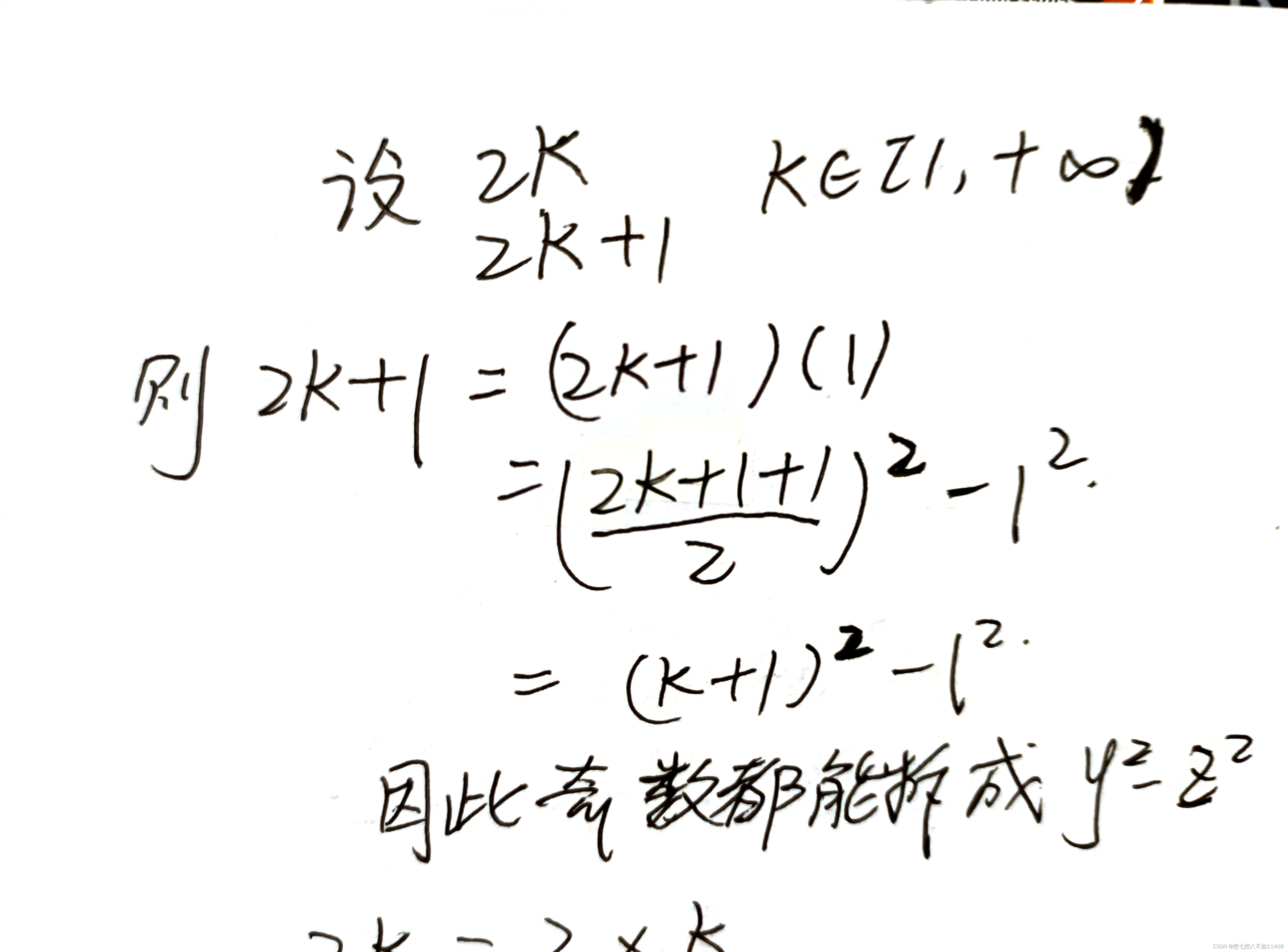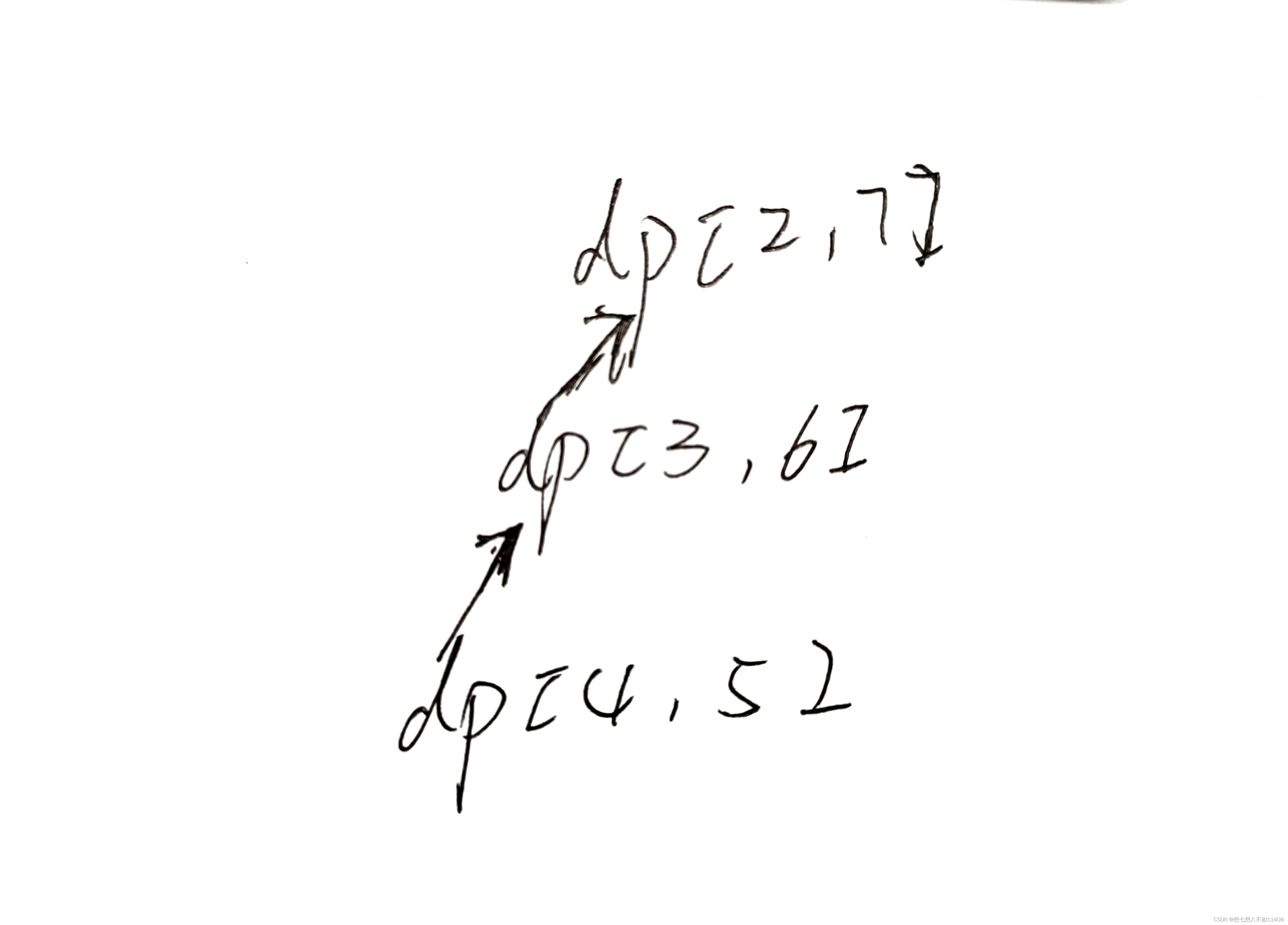蓝桥杯2023年第十四届省赛真题-平方差 - C语言网 (dotcpp.com)
初步想法,x = y2 − z2=(y+z)(y-z)
即x=a*b,a=y+z,b=y-z
2y=a+b
即a+b是2的倍数就好了。
即x存在两个因数之和为偶数就能满足条件。
但时间是(r-l)*x,数据1e9,直接T了
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
map<int,int> mp;
int cnt;
bool judge(int x)
{
for(int i=1;i<=x;i++)//找两个因数
{
if(x%i!=0) continue;
int d=x/i+i;
if(d%2==0||x==1)//说明是整数
{
return true;
}
}
return false;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int l,r;
cin>>l>>r;
for(int i=l;i<=r;i++)
{
if(judge(i)) cnt++;
}
cout<<cnt;
return 0;
}运行结果:

进一步分析:
根据题意多写几个,不难发现奇数似乎都能拆成y2 − z2的形式?因此,我们从奇偶的角度来找规律。
(这个地方写错了,是
那么,在这里就可以得出结论辣。想要数字能表示成y2-z2的形式,只有两种可能:
1.奇数 2.4的倍数
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int cnt;
signed main()
{
int l,r;
cin>>l>>r;
for(int i=l;i<=r;i++)
{
if(i%2) cnt++;
if(i%4==0) cnt++;
}
cout<<cnt;
return 0;
}
(这一步还不能过属实有点钻牛角尖了。。。。。
但是好在,已知一个数x,对应的奇数、4的倍数的数的个数是可以算出来的。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int cnt;
signed main()
{
int l,r;
cin>>l>>r;
int d=(l-1)/2;
if((l-1)%2==0) d--;
int p=l/4;
if((l%4)==0) p--;
cnt=(r-1)/2-d+r/4-p;
cout<<cnt;
return 0;
}蓝桥杯2023年第十四届省赛真题-更小的数 - C语言网 (dotcpp.com)
暴力
思路:
任取子串起点为i,终点为j。
然后运用双指针算法对子串进行判断。如果两边相等就往中间走。如果左边大了,说明这个子串反转后会变小;如果右边大了,说明这个子串反转后会变大。
#include<bits/stdc++.h>
using namespace std;
const int N=5e3+10;
string x;
int cnt;
signed main()
{
cin>>x;
for(int i=0;i<x.length();i++)
{
for(int j=i+1;j<x.length();j++)
{
int l=i,r=j;
while(l<=r)
{
if(x[l]<x[r]) break;
if(x[l]>x[r])
{
cnt++;
break;
}else l++,r--;
}
}
}
cout<<cnt;
return 0;
}暴力做法没想到在这个平台上直接过了,于是换了个平台P2070 - [蓝桥杯2023初赛] 更小的数 - New Online Judge (ecustacm.cn)
果然时间超限。。


DP
上面是三重循环,能想到的就是优化最后那一层while循环。
如果左边大了,说明这个子串反转后会变小;如果右边大了,说明这个子串反转后会变大。如果两边相等就l++,r--,这就意味着这种情况下当前这个字串的状态可以由较小的那一层决定。我们就可以想到DP。
稍微画一下就可以理解,dp[i][j]由dp[i+1][j-1]得到,因此最外面一层循环我们要从大到小,里面一层顺序无所谓,因为先得到dp[i+1][j]还是dp[i+1][j-1]对dp[i][j]没有任何影响。
#include<bits/stdc++.h>
using namespace std;
const int N=5e3+10;
string x;
int cnt;
int dp[N][N];
signed main()
{
cin>>x;
for(int i=x.length()-1;i>=0;i--)
{
for(int j=i+1;j<x.length();j++)
{
if(i>=j) continue;
if(x[i]>x[j]) dp[i][j]=1;
else if(x[i]==x[j]) dp[i][j]=dp[i+1][j-1];
cnt+=dp[i][j];
}
}
cout<<cnt;
return 0;
}蓝桥杯2023年第十四届省赛真题-颜色平衡树 - C语言网 (dotcpp.com)
暂时能力达不到。。。。